Прво ћемо разумети бинарно дрво и бинарно стабло претраге одвојено, а затим ћемо погледати разлике између бинарног стабла и бинарног стабла претраге.

Шта је бинарно дрво?

А Бинарно дрво јеПоказивач на лево дете:Чува референцу левог подређеног чвора.Показивач на право дете:Чува референцу десног подређеног чвора.Елемент података:Елемент података је вредност података коју чува чвор.

Бинарно стабло се може представити као:

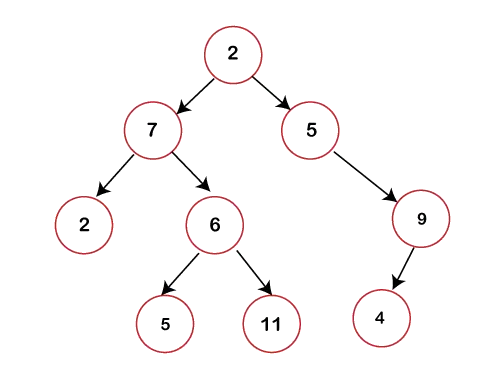
На горњој слици можемо приметити да сваки чвор садржи највише 2 детета. Ако било који чвор не садржи лево или десно дете онда би вредност показивача у односу на то дете била НУЛЛ.

Основне терминологије које се користе у бинарном стаблу су:

коренски чвор:Коренски чвор је први или највиши чвор у бинарном стаблу.Родитељски чвор:Када је чвор повезан са другим чвором преко ивица, тада је тај чвор познат као родитељски чвор. У бинарном стаблу, родитељски чвор може имати највише 2 детета.Подређени чвор:Ако чвор има свог претходника, онда је тај чвор познат као а дете чвор .Листни чвор:Чвор који не садржи дете познато као а лисни чвор .Унутрашњи чвор:Чвор који има најмање 2 деце познат као ан унутрашњи чвор .Дубина чвора:Удаљеност од коренског чвора до датог чвора је позната као а дубина чвора . Обезбеђујемо ознаке свим чворовима као што је основни чвор означен са 0 јер нема дубину, деца коренских чворова су означена са 1, деца коренског детета су означена са 2.Висина:Највећа удаљеност од коренског чвора до лисног чвора је висина чвора .

У бинарном стаблу постоји једно дрво познато као а савршено бинарно дрво . То је стабло у коме сви унутрашњи чворови морају да садрже два чвора, а сви чворови листа морају бити на истој дубини. У случају савршеног бинарног стабла, укупан број чворова који постоји у бинарном стаблу може се израчунати коришћењем следеће једначине:

н = 2^м+1-1

где је н број чворова, м је дубина чвора.

Шта је стабло бинарне претраге?

А Бинарно стабло претраге је стабло које следи неки редослед да би распоредило елементе, док бинарно стабло не прати никакав редослед. У стаблу бинарне претраге, вредност левог чвора мора бити мања од родитељског чвора, а вредност десног чвора мора бити већа од родитељског чвора.

Хајде да разумемо концепт бинарног стабла претраге кроз примере.

На горњој слици можемо приметити да је вредност коренског чвора 15, што је веће од вредности свих чворова у левом подстаблу. Вредност коренског чвора је мања од вредности свих чворова у десном подстаблу. Сада прелазимо на лево дете коренског чвора. 10 је веће од 8 и мање од 12; такође задовољава својство бинарног стабла претраге. Сада прелазимо на десно дете коренског чвора; вредност 20 је већа од 17 и мања од 25; такође задовољава својство бинарног стабла претраге. Стога можемо рећи да је стабло приказано изнад бинарно стабло претраге.

Сада, ако променимо вредност од 12 у 16 ​​у горњем бинарном стаблу, морамо да пронађемо да ли је то још увек бинарно стабло претраге или не.

Вредност коренског чвора је 15 што је веће од 10, али мање од 16, тако да не задовољава својство бинарног стабла претраге. Дакле, то није бинарно стабло претраге.

Операције на стаблу бинарног претраживања

Можемо извршити операције уметања, брисања и претраживања на бинарном стаблу претраге. Хајде да разумемо како се претрага врши на бинарној претрази. Бинарно стабло је приказано испод на којем морамо да извршимо операцију претраживања:

Претпоставимо да морамо да тражимо 10 у горњем бинарном стаблу. Да бисмо извршили бинарну претрагу, размотрићемо све целе бројеве у сортираном низу. Прво, креирамо комплетну листу у простору за претрагу и сви бројеви ће постојати у простору за претрагу. Простор за претрагу је означен са два показивача, односно почетак и крај. Низ горњег бинарног стабла се може представити као

Прво ћемо израчунати средњи елемент и упоредити средњи елемент са елементом који треба претраживати. Средњи елемент се израчунава коришћењем н/2. Вредност н је 7; дакле, средњи елемент је 15. Средњи елемент није једнак траженом елементу, тј. 10.

Напомена: Ако је елемент који се тражи мањи од средњег елемента, претрага ће се извршити у левој половини; у супротном, претрага ће се обавити на десној половини. У случају једнакости, елемент се налази.

Како је елемент који треба претраживати мањи од средњег елемента, тако ће се претрага вршити на левом низу. Сада је претрага смањена на половину, као што је приказано у наставку:

Средњи елемент у левом низу је 10, што је једнако траженом елементу.

Временска сложеност

У бинарном претраживању постоји н елемената. Ако средњи елемент није једнак траженом елементу, онда се простор за претрагу смањује на н/2, а ми ћемо наставити да смањујемо простор за претрагу за н/2 док не пронађемо елемент. У целој редукцији, ако пређемо са н на н/2 на н/4 и тако даље, онда ће бити потребно лог₂н корака.

Разлике између бинарног стабла и бинарног стабла претраге