У овом чланку ћемо разговарати о стаблу бинарног претраживања. Овај чланак ће бити веома користан и информативан студентима са техничким искуством јер је важна тема њиховог курса.
Пре него што пређемо директно на стабло бинарне претраге, хајде да прво погледамо кратак опис стабла.
Шта је дрво?
Стабло је врста структуре података која се користи за представљање података у хијерархијском облику. Може се дефинисати као колекција објеката или ентитета названих као чворови који су повезани заједно да симулирају хијерархију. Стабло је нелинеарна структура података пошто се подаци у стаблу не складиште линеарно или секвенцијално.
Сада, хајде да започнемо тему, стабло бинарне претраге.
Шта је стабло бинарне претраге?
Бинарно стабло претраге прати неки редослед за распоређивање елемената. У стаблу бинарне претраге, вредност левог чвора мора бити мања од родитељског чвора, а вредност десног чвора мора бити већа од родитељског чвора. Ово правило се рекурзивно примењује на лево и десно подстабло корена.
Хајде да разумемо концепт бинарног стабла претраге на примеру.
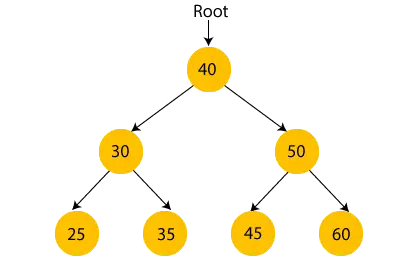
На горњој слици можемо приметити да је коренски чвор 40, и да су сви чворови левог подстабла мањи од коренског чвора, а сви чворови десног подстабла су већи од коренског чвора.
Слично, можемо видети да је лево дете коренског чвора веће од левог детета и мање од десног детета. Дакле, такође задовољава својство бинарног стабла претраге. Стога можемо рећи да је дрво на горњој слици бинарно стабло претраге.
Претпоставимо да ако променимо вредност чвора 35 у 55 у горњем стаблу, проверите да ли ће дрво бити бинарно стабло претраге или не.

У горњем стаблу, вредност коренског чвора је 40, што је веће од његовог левог подређеног 30, али мање од десног детета од 30, тј. 55. Дакле, горе наведено стабло не задовољава својство бинарног стабла претраге. Према томе, горе наведено стабло није бинарно стабло претраге.
Предности бинарног стабла претраге
- Претраживање елемента у бинарном стаблу претраге је лако јер увек имамо наговештај да које подстабло има жељени елемент.
- У поређењу са низом и повезаним листама, операције уметања и брисања су брже у БСТ-у.
Пример прављења бинарног стабла претраге
Сада, да видимо креирање бинарног стабла претраге користећи пример.
Претпоставимо да су елементи података - 45, 15, 79, 90, 10, 55, 12, 20, 50
- Прво, морамо да убацимо Четири, пет у дрво као корен дрвета.
- Затим, прочитајте следећи елемент; ако је мањи од коренског чвора, убаците га као корен левог подстабла и пређите на следећи елемент.
- У супротном, ако је елемент већи од коренског чвора, убаците га као корен десног подстабла.
Сада, да видимо процес креирања стабла бинарног претраживања користећи дати елемент података. Процес креирања БСТ-а је приказан испод -
израчунавање стажа у екцелу
Корак 1 - Убаците 45.

Корак 2 - Убаците 15.
Пошто је 15 мање од 45, убаците га као коренски чвор левог подстабла.

Корак 3 - Убаците 79.
Пошто је 79 веће од 45, убаците га као коренски чвор десног подстабла.

Корак 4 - Убаците 90.
90 је веће од 45 и 79, па ће бити уметнуто као десно подстабло од 79.

Корак 5 - Убаците 10.
10 је мање од 45 и 15, тако да ће бити уметнуто као лево подстабло од 15.

Корак 6 - Убаците 55.
55 је веће од 45 и мање од 79, тако да ће бити уметнуто као лево подстабло од 79.

Корак 7 - Убаците 12.
12 је мање од 45 и 15, али веће од 10, тако да ће бити уметнуто као десно подстабло од 10.

Корак 8 - Убаците 20.
20 је мање од 45, али веће од 15, тако да ће бити уметнуто као десно подстабло од 15.

Корак 9 - Убаците 50.
парафразирам ако по Радјарду Киплингу
50 је веће од 45, али мање од 79 и 55. Дакле, биће уметнуто као лево подстабло од 55.

Сада је креирање бинарног стабла претраге завршено. Након тога, пређимо на операције које се могу извршити на стаблу бинарног претраживања.
Можемо извршити операције уметања, брисања и претраживања на бинарном стаблу претраге.
Хајде да разумемо како се претрага врши на бинарном стаблу претраге.
Претраживање у бинарном стаблу претраге
Претраживање значи пронаћи или лоцирати одређени елемент или чвор у структури података. У бинарном стаблу претраге, претраживање чвора је лако јер се елементи у БСТ чувају у одређеном редоследу. Кораци претраживања чвора у стаблу бинарне претраге су наведени на следећи начин -
- Прво, упоредите елемент који се тражи са основним елементом стабла.
- Ако се роот подудара са циљним елементом, вратите локацију чвора.
- Ако се не подудара, онда проверите да ли је ставка мања од основног елемента, ако је мања од основног елемента, затим пређите на лево подстабло.
- Ако је већи од основног елемента, пређите на десно подстабло.
- Поновите горњу процедуру рекурзивно док се не пронађе подударање.
- Ако елемент није пронађен или није присутан у стаблу, вратите НУЛЛ.
Сада, хајде да разумемо претрагу у бинарном стаблу користећи пример. Узимамо стабло бинарног претраживања формирано изнад. Претпоставимо да морамо да пронађемо чвор 20 са стабла испод.
Корак 1:

Корак 2:

Корак 3:

Сада, да видимо алгоритам за претрагу елемента у стаблу бинарне претраге.
Алгоритам за претрагу елемента у бинарном стаблу претраге
Search (root, item) Step 1 - if (item = root → data) or (root = NULL) return root else if (item <root 2 → data) return search(root left, item) else right, end if step - < pre> <p>Now let's understand how the deletion is performed on a binary search tree. We will also see an example to delete an element from the given tree.</p> <h3>Deletion in Binary Search tree</h3> <p>In a binary search tree, we must delete a node from the tree by keeping in mind that the property of BST is not violated. To delete a node from BST, there are three possible situations occur -</p> <ul> <li>The node to be deleted is the leaf node, or,</li> <li>The node to be deleted has only one child, and,</li> <li>The node to be deleted has two children</li> </ul> <p>We will understand the situations listed above in detail.</p> <p> <strong>When the node to be deleted is the leaf node</strong> </p> <p>It is the simplest case to delete a node in BST. Here, we have to replace the leaf node with NULL and simply free the allocated space.</p> <p>We can see the process to delete a leaf node from BST in the below image. In below image, suppose we have to delete node 90, as the node to be deleted is a leaf node, so it will be replaced with NULL, and the allocated space will free.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-15.webp" alt="Binary Search tree"> <p> <strong>When the node to be deleted has only one child</strong> </p> <p>In this case, we have to replace the target node with its child, and then delete the child node. It means that after replacing the target node with its child node, the child node will now contain the value to be deleted. So, we simply have to replace the child node with NULL and free up the allocated space.</p> <p>We can see the process of deleting a node with one child from BST in the below image. In the below image, suppose we have to delete the node 79, as the node to be deleted has only one child, so it will be replaced with its child 55.</p> <p>So, the replaced node 79 will now be a leaf node that can be easily deleted.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-16.webp" alt="Binary Search tree"> <p> <strong>When the node to be deleted has two children</strong> </p> <p>This case of deleting a node in BST is a bit complex among other two cases. In such a case, the steps to be followed are listed as follows -</p> <ul> <li>First, find the inorder successor of the node to be deleted.</li> <li>After that, replace that node with the inorder successor until the target node is placed at the leaf of tree.</li> <li>And at last, replace the node with NULL and free up the allocated space.</li> </ul> <p>The inorder successor is required when the right child of the node is not empty. We can obtain the inorder successor by finding the minimum element in the right child of the node.</p> <p>We can see the process of deleting a node with two children from BST in the below image. In the below image, suppose we have to delete node 45 that is the root node, as the node to be deleted has two children, so it will be replaced with its inorder successor. Now, node 45 will be at the leaf of the tree so that it can be deleted easily.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-17.webp" alt="Binary Search tree"> <p>Now let's understand how insertion is performed on a binary search tree.</p> <h3>Insertion in Binary Search tree</h3> <p>A new key in BST is always inserted at the leaf. To insert an element in BST, we have to start searching from the root node; if the node to be inserted is less than the root node, then search for an empty location in the left subtree. Else, search for the empty location in the right subtree and insert the data. Insert in BST is similar to searching, as we always have to maintain the rule that the left subtree is smaller than the root, and right subtree is larger than the root.</p> <p>Now, let's see the process of inserting a node into BST using an example.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-18.webp" alt="Binary Search tree"> <br> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-19.webp" alt="Binary Search tree"> <h3>The complexity of the Binary Search tree</h3> <p>Let's see the time and space complexity of the Binary search tree. We will see the time complexity for insertion, deletion, and searching operations in best case, average case, and worst case.</p> <h3>1. Time Complexity</h3> <table class="table"> <tr> <th>Operations</th> <th>Best case time complexity</th> <th>Average case time complexity</th> <th>Worst case time complexity</th> </tr> <tr> <td> <strong>Insertion</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> <tr> <td> <strong>Deletion</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> <tr> <td> <strong>Search</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> </table> <p>Where 'n' is the number of nodes in the given tree.</p> <h3>2. Space Complexity</h3> <table class="table"> <tr> <th>Operations</th> <th>Space complexity</th> </tr> <tr> <td> <strong>Insertion</strong> </td> <td>O(n)</td> </tr> <tr> <td> <strong>Deletion</strong> </td> <td>O(n)</td> </tr> <tr> <td> <strong>Search</strong> </td> <td>O(n)</td> </tr> </table> <ul> <li>The space complexity of all operations of Binary search tree is O(n).</li> </ul> <h2>Implementation of Binary search tree</h2> <p>Now, let's see the program to implement the operations of Binary Search tree.</p> <p> <strong>Program:</strong> Write a program to perform operations of Binary Search tree in C++.</p> <p>In this program, we will see the implementation of the operations of binary search tree. Here, we will see the creation, inorder traversal, insertion, and deletion operations of tree.</p> <p>Here, we will see the inorder traversal of the tree to check whether the nodes of the tree are in their proper location or not. We know that the inorder traversal always gives us the data in ascending order. So, after performing the insertion and deletion operations, we perform the inorder traversal, and after traversing, if we get data in ascending order, then it is clear that the nodes are in their proper location.</p> <pre> #include using namespace std; struct Node { int data; Node *left; Node *right; }; Node* create(int item) { Node* node = new Node; node->data = item; node->left = node->right = NULL; return node; } /*Inorder traversal of the tree formed*/ void inorder(Node *root) { if (root == NULL) return; inorder(root->left); //traverse left subtree cout<data <right); traverse right subtree } node* findminimum(node* cur) *to find the inorder successor* { while(cur->left != NULL) { cur = cur->left; } return cur; } Node* insertion(Node* root, int item) /*Insert a node*/ { if (root == NULL) return create(item); /*return new node if tree is empty*/ if (item data) root->left = insertion(root->left, item); else root->right = insertion(root->right, item); return root; } void search(Node* &cur, int item, Node* &parent) { while (cur != NULL && cur->data != item) { parent = cur; if (item data) cur = cur->left; else cur = cur->right; } } void deletion(Node*& root, int item) /*function to delete a node*/ { Node* parent = NULL; Node* cur = root; search(cur, item, parent); /*find the node to be deleted*/ if (cur == NULL) return; if (cur->left == NULL && cur->right == NULL) /*When node has no children*/ { if (cur != root) { if (parent->left == cur) parent->left = NULL; else parent->right = NULL; } else root = NULL; free(cur); } else if (cur->left && cur->right) { Node* succ = findMinimum(cur->right); int val = succ->data; deletion(root, succ->data); cur->data = val; } else { Node* child = (cur->left)? cur->left: cur->right; if (cur != root) { if (cur == parent->left) parent->left = child; else parent->right = child; } else root = child; free(cur); } } int main() { Node* root = NULL; root = insertion(root, 45); root = insertion(root, 30); root = insertion(root, 50); root = insertion(root, 25); root = insertion(root, 35); root = insertion(root, 45); root = insertion(root, 60); root = insertion(root, 4); printf('The inorder traversal of the given binary tree is -
'); inorder(root); deletion(root, 25); printf('
After deleting node 25, the inorder traversal of the given binary tree is -
'); inorder(root); insertion(root, 2); printf('
After inserting node 2, the inorder traversal of the given binary tree is -
'); inorder(root); return 0; } </data></pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-20.webp" alt="Binary Search tree"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></root> Излаз
Након извршења горњег кода, излаз ће бити -

Дакле, то је све о чланку. Надамо се да ће вам чланак бити користан и информативан.
