Делете функција се користи за брисање наведеног чвора из бинарног стабла претраге. Међутим, морамо да избришемо чвор из бинарног стабла претраге на такав начин, да својство бинарног стабла претраге не наруши. Постоје три ситуације брисања чвора из бинарног стабла претраге.
инсталирај мавен
Чвор који треба избрисати је лисни чвор
То је најједноставнији случај, у овом случају замените лисни чвор са НУЛЛ и једноставно ослободите додељени простор.
На следећој слици бришемо чвор 85, пошто је чвор лисни чвор, стога ће чвор бити замењен са НУЛЛ и додељени простор ће бити ослобођен.
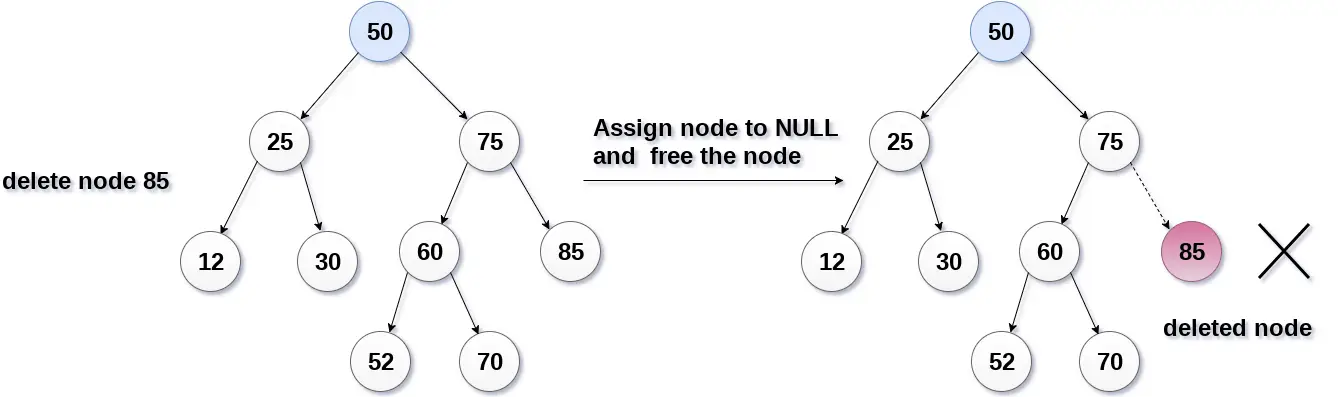
Чвор који треба избрисати има само једно дете.
У овом случају, замените чвор његовим дететом и избришите подређени чвор, који сада садржи вредност коју треба избрисати. Једноставно га замените са НУЛЛ и ослободите додељени простор.
јава цхар у стринг
На следећој слици, чвор 12 треба обрисати. Има само једно дете. Чвор ће бити замењен његовим подређеним чвором и замењени чвор 12 (који је сада лисни чвор) ће једноставно бити обрисан.

Чвор који треба избрисати има двоје деце.
То је мало сложен случај у поређењу са друга два случаја. Међутим, чвор који треба обрисати се рекурзивно замењује његовим редоследом или претходником све док се вредност чвора (која треба обрисати) не постави на лист стабла. Након процедуре, замените чвор са НУЛЛ и ослободите додељени простор.
На следећој слици треба избрисати чвор 50 који је коренски чвор стабла. Прелазак стабла у редоследу дат у наставку.
апликације рачунарства у облаку
6, 25, 30, 50, 52, 60, 70, 75.
замени 50 његовим наследником 52. Сада ће 50 бити померено на лист дрвета, које ће једноставно бити избрисано.

Алгоритам
Избриши (ДРВО, СТАВКА)
Упишите 'ставка није пронађена у стаблу' ЕЛСЕ АКО ПОДАЦИ СТАВКЕ
Избриши (ДРВО->ЛЕВО, СТАВКА)
ЕЛСЕ ИФ СТАВКА > ДРВО -> ПОДАЦИ
Избриши (ДРВО -> ДЕСНО, СТАВКА)
ЕЛСЕ ИФ ДРВО -> ЛЕВО И ДРВО -> ДЕСНО
СЕТ ТЕМП = финдЛаргестНоде(ТРЕЕ -> ЛЕФТ)
ПОСТАВИ ДРВО -> ПОДАЦИ = ТЕМП -> ПОДАЦИ
Избриши (ДРВО -> ЛИЈЕВО, ТЕМП -> ПОДАЦИ)
ЕЛСЕ
СЕТ ТЕМП = ДРВО
АКО ДРВО -> ЛЕВО = НУЛЛ И ДРВО -> ДЕСНО = НУЛЛ
СЕТ ТРЕЕ = НУЛЛ
ЕЛСЕ ИФ ТРЕЕ -> ЛЕФТ != НУЛЛ
ПОСТАВИ ДРВО = ДРВО -> ЛЕВО
ЕЛСЕ
ПОСТАВИ ДРВО = ДРВО -> ДЕСНО
[КРАЈ АКО]
ФРЕЕ ТЕМП
[КРАЈ АКО]
Функција:
void deletion(Node*& root, int item) { Node* parent = NULL; Node* cur = root; search(cur, item, parent); if (cur == NULL) return; if (cur->left == NULL && cur->right == NULL) { if (cur != root) { if (parent->left == cur) parent->left = NULL; else parent->right = NULL; } else root = NULL; free(cur); } else if (cur->left && cur->right) { Node* succ = findMinimum(cur- >right); int val = succ->data; deletion(root, succ->data); cur->data = val; } else { Node* child = (cur->left)? Cur- >left: cur->right; if (cur != root) { if (cur == parent->left) parent->left = child; else parent->right = child; } else root = child; free(cur); } } Node* findMinimum(Node* cur) { while(cur->left != NULL) { cur = cur->left; } return cur; } 