Стацк је линеарна структура података која прати ЛИФО (последњи-први-изишао) принцип. Стек има један крај, док ред има два краја ( напред и позади ). Садржи само један показивач горњи показивач показујући на највиши елемент стека. Кад год се елемент дода у стек, он се додаје на врх стека, а елемент се може избрисати само из стека. Другим речима, а стек се може дефинисати као контејнер у коме се уметање и брисање може вршити са једног краја познатог као врх стека.

Неке кључне тачке у вези са стеком

• Зове се као стог јер се понаша као хрпа у стварном свету, гомиле књига итд.
• Стацк је апстрактни тип података са унапред дефинисаним капацитетом, што значи да може да складишти елементе ограничене величине.
• То је структура података која прати неки редослед за уметање и брисање елемената, а тај редослед може бити ЛИФО или ФИЛО.

Рад стека

Стацк ради на ЛИФО шаблону. Као што можемо приметити на слици испод, постоји пет меморијских блокова у стеку; према томе, величина стека је 5.

је протеинска маст

Претпоставимо да желимо да ускладиштимо елементе у стеку и претпоставимо да је стек празан. Узели смо сноп величине 5 као што је приказано испод у којем гурамо елементе један по један док се сноп не напуни.

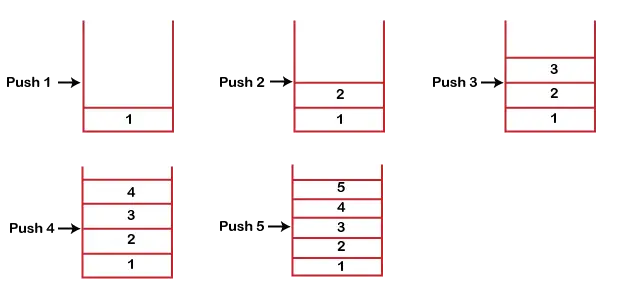
Пошто је наш стек пун пошто је величина стека 5. У горњим случајевима можемо приметити да иде од врха ка дну када смо уносили нови елемент у стек. Гомила се пуни од дна до врха.

Када извршимо операцију брисања на стеку, постоји само један начин за улазак и излазак пошто је други крај затворен. Следи ЛИФО образац, што значи да ће вредност која је прва унета бити уклоњена последња. У наведеном случају прво се уписује вредност 5, па ће бити уклоњена тек након брисања свих осталих елемената.

Стандардне операције стека

Следе неке уобичајене операције које се примењују на стеку:

пусх():Када уметнемо елемент у стек, операција је позната као гурање. Ако је стек пун, долази до стања преливања.поп():Када избришемо елемент из стека, операција је позната као поп. Ако је стек празан значи да ниједан елемент не постоји у стеку, ово стање је познато као недовољно стање.Празно():Одређује да ли је стек празан или не.је пун():Он одређује да ли је стек пун или не.'завирити():Враћа елемент на датој позицији.цоунт():Враћа укупан број доступних елемената у стеку.промени():Мења елемент на датој позицији.приказ():Штампа све елементе доступне у стеку.

ПУСХ операција

Кораци укључени у ПУСХ операцију су дати у наставку:

• Пре него што убацимо елемент у стек, проверавамо да ли је стек пун.
• Ако покушамо да убацимо елемент у стек, а стек је пун, онда је преливати настаје стање.
• Када иницијализујемо стек, постављамо вредност топ као -1 да бисмо проверили да ли је стек празан.
• Када се нови елемент гурне у стек, прво се повећава вредност врха, тј. топ=топ+1, а елемент ће бити постављен на нову позицију топ .
• Елементи ће бити уметнути док не дођемо до мак величина стека.

ПОП операција

Кораци укључени у ПОП операцију су дати у наставку:

фореацх лооп типесцрипт

• Пре брисања елемента из стека, проверавамо да ли је стек празан.
• Ако покушамо да избришемо елемент из празног стека, онда се ундерфлов настаје стање.
• Ако стек није празан, прво приступамо елементу на који указује топ
• Када се изврши искакање, врх се смањује за 1, тј. топ=топ-1 .

Апплицатионс оф Стацк

Следеће су апликације стека:

Балансирање симбола:Стацк се користи за балансирање симбола. На пример, имамо следећи програм:

 int main() { cout&lt;<'hello'; cout<<'javatpoint'; } < pre> <p>As we know, each program has <em>an opening</em> and <em>closing</em> braces; when the opening braces come, we push the braces in a stack, and when the closing braces appear, we pop the opening braces from the stack. Therefore, the net value comes out to be zero. If any symbol is left in the stack, it means that some syntax occurs in a program.</p> <ul> <tr><td>String reversal:</td> Stack is also used for reversing a string. For example, we want to reverse a &apos; <strong>javaTpoint</strong> &apos; string, so we can achieve this with the help of a stack. <br> First, we push all the characters of the string in a stack until we reach the null character. <br> After pushing all the characters, we start taking out the character one by one until we reach the bottom of the stack. </tr><tr><td>UNDO/REDO:</td> It can also be used for performing UNDO/REDO operations. For example, we have an editor in which we write &apos;a&apos;, then &apos;b&apos;, and then &apos;c&apos;; therefore, the text written in an editor is abc. So, there are three states, a, ab, and abc, which are stored in a stack. There would be two stacks in which one stack shows UNDO state, and the other shows REDO state. <br> If we want to perform UNDO operation, and want to achieve &apos;ab&apos; state, then we implement pop operation. </tr><tr><td>Recursion:</td> The recursion means that the function is calling itself again. To maintain the previous states, the compiler creates a system stack in which all the previous records of the function are maintained. </tr><tr><td>DFS(Depth First Search):</td> This search is implemented on a Graph, and Graph uses the stack data structure. </tr><tr><td>Backtracking:</td> Suppose we have to create a path to solve a maze problem. If we are moving in a particular path, and we realize that we come on the wrong way. In order to come at the beginning of the path to create a new path, we have to use the stack data structure. </tr><tr><td>Expression conversion:</td> Stack can also be used for expression conversion. This is one of the most important applications of stack. The list of the expression conversion is given below: <pre>Infix to prefix Infix to postfix Prefix to infix Prefix to postfix Postfix to infix</pre> </tr><tr><td>Memory management:</td> The stack manages the memory. The memory is assigned in the contiguous memory blocks. The memory is known as stack memory as all the variables are assigned in a function call stack memory. The memory size assigned to the program is known to the compiler. When the function is created, all its variables are assigned in the stack memory. When the function completed its execution, all the variables assigned in the stack are released. </tr></ul> <hr></'hello';>