Релациона алгебра је процедурални језик упита. Даје процес корак по корак за добијање резултата упита. Користи операторе за обављање упита.
Врсте релационих операција
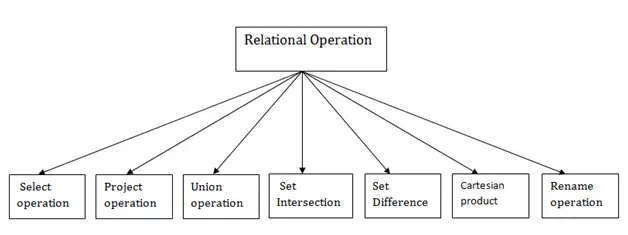
1. Изаберите Операцију:
- Операција одабира бира торке који задовољавају дати предикат.
- Означава се са сигма (σ).
Notation: σ p(r)
Где:
стр се користи за предвиђање избора
р се користи за однос
стр се користи као пропозициона логичка формула која може да користи конекторе као што су: И ИЛИ и НЕ. Ови релациони се могу користити као релациони оператори као што су =, =, ≧, , ≦.
На пример: ЛОАН Релатион
| БРАНЦХ_НАМЕ | ЛОАН_НО | ИЗНОС |
|---|---|---|
| Центар града | Л-17 | 1000 |
| Секвоја | Л-23 | 2000 |
| Перририде | Л-15 | 1500 |
| Центар града | Л-14 | 1500 |
| Мианус | Л-13 | 500 |
| Роундхилл | Л-11 | 900 |
| Перририде | Л-16 | 1300 |
Улазни:
σ BRANCH_NAME='perryride' (LOAN)
Излаз:
множење матрице у в
| БРАНЦХ_НАМЕ | ЛОАН_НО | ИЗНОС |
|---|---|---|
| Перририде | Л-15 | 1500 |
| Перририде | Л-16 | 1300 |
2. Операција пројекта:
- Ова операција приказује листу оних атрибута које желимо да прикажемо у резултату. Остали атрибути су елиминисани из табеле.
- Означава се са ∏.
Notation: ∏ A1, A2, An (r)
Где
А1 , А2 , А3 се користи као име атрибута релације р .
Пример: ОДНОС СА КЛИЈЕНТАМА
| НАМЕ | СТРЕЕТ | ГРАД |
|---|---|---|
| Јонес | Главни | Харисон |
| Смитх | Север | Раж |
| Хаис | Главни | Харисон |
| Цурри | Север | Раж |
| Јохнсон | Соул | Бруклин |
| Броокс | Сенаторе | Бруклин |
Улазни:
∏ NAME, CITY (CUSTOMER)
Излаз:
| НАМЕ | ГРАД |
|---|---|
| Јонес | Харисон |
| Смитх | Раж |
| Хаис | Харисон |
| Цурри | Раж |
| Јохнсон | Бруклин |
| Броокс | Бруклин |
3. Синдикална операција:
- Претпоставимо да постоје две торке Р и С. Операција уједињења садржи све торке који су или у Р или С или оба у Р&С.
- Он елиминише дупликате тупле. Означава се са ∪.
Notation: R ∪ S
Синдикална операција мора да испуњава следеће услове:
- Р и С морају имати атрибут истог броја.
- Дупликати тупле се аутоматски елиминишу.
Пример:
ОДНОС ДЕПОСИТОРА
мл у оз
| ИМЕ КЛИЈЕНТА | РАЧУН БР |
|---|---|
| Јохнсон | А-101 |
| Смитх | А-121 |
| Маиес | А-321 |
| Турнер | А-176 |
| Јохнсон | А-273 |
| Јонес | А-472 |
| Линдзи | А-284 |
ЗАЈМЉЕНИ ОДНОСИ
| ИМЕ КЛИЈЕНТА | ЛОАН_НО |
|---|---|
| Јонес | Л-17 |
| Смитх | Л-23 |
| Хаиес | Л-15 |
| Јацксон | Л-14 |
| Цурри | Л-93 |
| Смитх | Л-11 |
| Виллиамс | Л-17 |
Улазни:
∏ CUSTOMER_NAME (BORROW) ∪ ∏ CUSTOMER_NAME (DEPOSITOR)
Излаз:
| ИМЕ КЛИЈЕНТА |
|---|
| Јохнсон |
| Смитх |
| Хаиес |
| Турнер |
| Јонес |
| Линдзи |
| Јацксон |
| Цурри |
| Виллиамс |
| Маиес |
4. Поставите раскрсницу:
- Претпоставимо да постоје две торке Р и С. Операција пресека скупа садржи све торке који се налазе у оба Р и С.
- Означава се пресеком ∩.
Notation: R ∩ S
Пример: Користећи горњу табелу ДЕПОЗИТАР и табелу ЗАЈМИЦЕ
Улазни:
∏ CUSTOMER_NAME (BORROW) ∩ ∏ CUSTOMER_NAME (DEPOSITOR)
Излаз:
структуре које користе низове у ц
| ИМЕ КЛИЈЕНТА |
|---|
| Смитх |
| Јонес |
5. Поставите разлику:
- Претпоставимо да постоје две торке Р и С. Операција пресека скупа садржи све скупове који су у Р али нису у С.
- Означава се пресеком минус (-).
Notation: R - S
Пример: Користећи горњу табелу ДЕПОЗИТАР и табелу ЗАЈМИЦЕ
Улазни:
∏ CUSTOMER_NAME (BORROW) - ∏ CUSTOMER_NAME (DEPOSITOR)
Излаз:
| ИМЕ КЛИЈЕНТА |
|---|
| Јацксон |
| Хаиес |
| Виллиамс |
| Цурри |
6. Декартов производ
- Декартов производ се користи за комбиновање сваког реда у једној табели са сваким редом у другој табели. Такође је познат као унакрсни производ.
- Означава се са Кс.
Notation: E X D
Пример:
ЗАПОСЛЕНИ
| ЕМП_ИД | ЕМП_НАМЕ | ЕМП_ДЕПТ |
|---|---|---|
| 1 | Смитх | А |
| 2 | Харри | Ц |
| 3 | Јохн | Б |
ОДЕЉЕЊЕ
| ДЕПТ_НО | ДЕПТ_НАМЕ |
|---|---|
| А | Маркетинг |
| Б | Продаја |
| Ц | Правни |
Улазни:
EMPLOYEE X DEPARTMENT
Излаз:
како претворити стринг у инт
| ЕМП_ИД | ЕМП_НАМЕ | ЕМП_ДЕПТ | ДЕПТ_НО | ДЕПТ_НАМЕ |
|---|---|---|---|---|
| 1 | Смитх | А | А | Маркетинг |
| 1 | Смитх | А | Б | Продаја |
| 1 | Смитх | А | Ц | Правни |
| 2 | Харри | Ц | А | Маркетинг |
| 2 | Харри | Ц | Б | Продаја |
| 2 | Харри | Ц | Ц | Правни |
| 3 | Јохн | Б | А | Маркетинг |
| 3 | Јохн | Б | Б | Продаја |
| 3 | Јохн | Б | Ц | Правни |
7. Операција преименовања:
Операција преименовања се користи за преименовање излазне релације. Означава се са рхо (п).
Пример: Можемо користити оператор преименовања да преименујемо релацију СТУДЕНТ у СТУДЕНТ1.
ρ(STUDENT1, STUDENT)
