Акутни, тупи, једнакокраки, једнакострани... Када је реч о троугловима, постоји много различитих варијанти, али само неколико 'посебних'. Ови посебни троуглови имају стране и углове који су конзистентни и предвидљиви и могу се користити за пречицу кроз ваше проблеме геометрије или тригонометрије. А троугао 30-60-90 — који се изговара као „тридесет шездесет деведесет“ — је заиста посебан тип троугла.

У овом водичу ћемо вас провести кроз шта је троугао 30-60-90, зашто функционише и када (и како) да искористите своје знање о њему. Па да пређемо на то!

Шта је троугао 30-60-90?

Троугао 30-60-90 је посебан правоугли троугао (правоугли троугао је било који троугао који садржи угао од 90 степени) који увек има степене углове од 30 степени, 60 степени и 90 степени. Пошто је то посебан троугао, он такође има вредности дужине странице које су увек у доследном односу једна са другом.

Основни однос троугла 30-60-90 је:

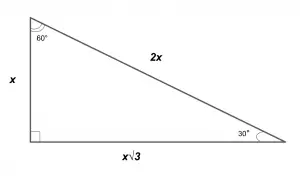
Страна насупрот угла од 30°: $к$

Страна насупрот угла од 60°: $к * √3$

Страна насупрот угла од 90°: к$

На пример, троугао од 30-60-90 степени може имати дужину страница од:

2, 2√3, 4

7, 7√3, 14

√3, 3, 2√3

селен туториал јава

(Зашто је дужи крак 3? У овом троуглу, најкраћи крак ($к$) је $√3$, па је за дужу ногу $к√3 = √3 * √3 = √9 = 3$. И хипотенуза је 2 пута најкраћа крака, или √3$)

И тако даље.

Страна наспрам угла од 30° је увек најмања , јер је 30 степени најмањи угао. Страна насупрот угла од 60° биће средња дужина , јер је 60 степени угао средње величине у овом троуглу. И, коначно, страна наспрам угла од 90° увек ће бити највећа страница (хипотенуза) јер је 90 степени највећи угао.

Иако може изгледати слично другим врстама правоуглог троугла, разлог зашто је троугао 30-60-90 толико посебан је тај што су вам потребне само три информације да бисте пронашли свако друго мерење. Све док знате вредност две мере угла и дужине једне стране (није важно која страна), знате све што треба да знате о свом троуглу.

На пример, можемо користити формулу троугла 30-60-90 да попунимо све преостале празне информације у троугловима испод.

Пример 1

Видимо да је ово правоугли троугао у коме је хипотенуза двоструко већа од једне од катета. То значи да ово мора бити троугао 30-60-90 и да је мања страна насупрот 30°.

Дужа нога, према томе, мора бити насупрот угла од 60° и мери * √3$, или √3$.

Пример 2

кор у јава

Видимо да ово мора бити троугао 30-60-90 јер можемо видети да је ово правоугли троугао са једним датим мерењем, 30°. Неозначени угао тада мора бити 60°.

Пошто је 18 мера насупрот угла од 60°, мора бити једнако $к√3$. Најкраћа нога тада мора да мери 18$/√3$.

(Имајте на уму да ће дужина ноге заправо бити /{√3} * {√3}/{√3} = {18√3}/3 = 6√3$ јер именилац не може да садржи радикал/квадратни корен).

А хипотенуза ће бити (18/√3)$

(Имајте на уму да, опет, не можете имати радикал у имениоцу, тако да ће коначни одговор заиста бити 2 пута дужи од ноге од √3$ => √3$).

Пример 3

Опет су нам дата два мерења угла (90° и 60°), тако да ће трећа мера бити 30°. Пошто је ово троугао 30-60-90 и хипотенуза је 30, најкраћи крак ће бити једнак 15, а дужи 15√3.

Нема потребе да консултујете магичну осмицу — ова правила увек функционишу.

Зашто функционише: 30-60-90 Доказ теореме троугла

Али зашто овај посебан троугао функционише на начин на који ради? Како знамо да су ова правила законита? Хајде да прођемо кроз тачно како функционише теорема троугла 30-60-90 и докажемо зашто ће ове дужине страница увек бити конзистентне.

Прво, заборавимо на правоуглове троугле на секунду и погледајмо а једнакостранични троугао.

Једнакостранични троугао је троугао који има све једнаке странице и све једнаке углове. Пошто унутрашњи углови троугла увек износе 180° и 0/3 = 60$, једнакостранични троугао ће увек имати три угла од 60°.

Сада спустимо висину од највишег угла до основе троугла.

Сада смо створио два права угла и два подударна (једнака) троугла.

Како знамо да су једнаки троуглови? Зато што смо пали са висине једнакостраничан троугла, поделили смо основу тачно на пола. Нови троуглови такође деле једну страну (висину) и сваки од њих има исту дужину хипотенузе. Пошто деле три заједничке дужине страница (ССС), то значи троуглови су подударни.

Напомена: не само да су два троугла подударна на основу принципа дужине бочне стране, или ССС, већ и засноване на мерама бочне стране угла (САС), угао-угао-стране (ААС) и угао- бочни угао (АСА). У основи? Они су дефинитивно подударни.

Сада када смо доказали подударност два нова троугла, можемо видети да сваки горњи угл мора бити једнак 30 степени (јер сваки троугао већ има углове од 90° и 60° и мора да има збир до 180°). Ово значи направили смо два троугла 30-60-90.

И пошто знамо да смо основу једнакостраничног троугла пресекли на пола, можемо видети да је страна насупрот угла од 30° (најкраћа страница) сваког од наших троуглова 30-60-90 тачно половина дужине хипотенузе .

Дакле, назовимо нашу првобитну дужину странице $к$ и нашу преполовљену дужину $к/2$.

Сада све што нам преостаје је да пронађемо дужину наше средње стране коју деле два троугла. Да бисмо то урадили, можемо једноставно користити Питагорину теорему.

$а^2 + б^2 = ц^2$

$(к/2)^2 + б^2 = к^2$

$б^2 = к^2 - ({к^2}/4)$

$б^2 = {4к^2}/4 - {к^2}/4$

$б^2 = {3к^2}/4$

$б = {√3к}/2$

пд.мерге

Дакле, остаје нам: $к/2, {к√3}/2, к$

Сада помножимо сваку меру са 2, само да бисмо олакшали живот и избегли све разломке. На тај начин, остаје нам:

$к$, $к√3$, к$

Видимо, дакле, да ће троугао 30-60-90 увек имају конзистентне дужине страница од $к$, $к√3$ и к$ (или $к/2$, ${√3к}/2$ и $к$).

Срећом по нас, можемо доказати да су правила троугла 30-60-90 истинита без свега овога.

Када користити правила троугла 30-60-90

Познавање правила троугла 30-60-90 моћи ће да вам уштеди време и енергију на мноштву различитих математичких задатака, односно широком спектру проблема геометрије и тригонометрије.

Геометрија

Правилно разумевање троуглова 30-60-90 ће вам омогућити да решите геометријска питања која би било немогуће решити без познавања ових правила односа, или би у најмању руку било потребно доста времена и труда да се реши 'дуг пут'.

Са посебним односима троугла, можете да одредите недостајуће висине троугла или дужине крака (без потребе да користите Питагорину теорему), пронађете површину троугла користећи недостајуће информације о висини или основној дужини и брзо израчунате периметре.

Сваки пут када вам је потребна брзина да одговорите на питање, памћење пречица као што су ваша правила 30-60-90 ће вам добро доћи.

Тригонометрија

Памћење и разумевање односа троугла 30-60-90 такође ће вам омогућити да решите многе тригонометријске проблеме без потребе за калкулатором или потребе да своје одговоре апроксимирате у децималном облику.

Троугао 30-60-90 има прилично једноставне синусе, косинусе и тангенте за сваки угао (а ова мерења ће увек бити конзистентна).

Синус од 30° ће увек бити /2$.

инт удвостручити

Косинус од 60° ће увек бити /2$.

Иако су остали синуси, косинуси и тангенте прилично једноставни, ово су два која је најлакше запамтити и вероватно ће се појавити на тестовима. Дакле, познавање ових правила ће вам омогућити да пронађете ова тригонометријска мерења што је брже могуће.

Савети за памћење правила 30-60-90

Знате да су ова правила односа 30-60-90 корисна, али како задржати информације у својој глави? Сећање на правила троугла 30-60-90 је ствар памћења односа 1: √3 : 2 и сазнања да је најкраћа дужина странице увек насупрот најкраћем углу (30°), а да је најдужа дужина странице увек насупрот највећи угао (90°).

Неки људи памте однос мислећи: ' $би к$, $бо 2 би к$, $би к бо √ бо3$, ' јер је низ '1, 2, 3' обично лако запамтити. Једина мера предострожности за коришћење ове технике је да запамтите да је најдужа страна заправо к$, не $к$ пута $√3$.

Други начин да запамтите своје односе је да користите мнемоничку игру речи у односу 1: корен 3: 2 у њиховом правилном редоследу. На пример, „Џеки Мичел је избацио Лу Герига и „освојио и Рути“,“: један, корен три, два. (И то је права чињеница из историје бејзбола!)

Поиграјте се сопственим мнемоничким уређајима ако вам се не свиђају — отпевајте однос према песми, пронађите сопствене фразе „један, корен три, два“ ​​или смислите песму о односу. Можете чак и да се сетите да је троугао 30-60-90 пола једнакостраничан и одатле израчунајте мере ако не волите да их запамтите.

Међутим, има смисла да запамтите ова правила 30-60-90, задржите те односе у глави за ваша будућа питања геометрије и тригонометрије.

Памћење је ваш пријатељ, али то можете учинити.

Пример 30-60-90 Питања

Сада када смо погледали како и зашто троуглова 30-60-90, хајде да прорадимо кроз неке проблеме у пракси.

Геометрија

Грађевински радник наслања мердевине од 40 стопа уз бочну страну зграде под углом од 30 степени у односу на земљу. Земља је равна, а страна зграде је окомита на тло. Колико далеко до зграде досежу мердевине, до најближе стопе?

Без познавања наших специјалних правила троугла 30-60-90, морали бисмо да користимо тригонометрију и калкулатор да пронађемо решење за овај проблем, пошто имамо само једну страну троугла. Али пошто знамо да је ово а посебан троугла, можемо пронаћи одговор за само неколико секунди.

Ако су зграда и тло окомити једни на друге, то мора да значи да зграда и тло чине прави угао (90°). Такође је дато да се мердевине сусрећу са тлом под углом од 30°. Стога можемо видети да преостали угао мора бити 60°, што ово чини троуглом 30-60-90.

Сада знамо да је хипотенуза (најдужа страна) овог 30-60-90 40 стопа, што значи да ће најкраћа страна бити половина те дужине. (Запамтите да је најдужа страна увек два пута—к$—дужа од најкраће стране.) Пошто је најкраћа страна наспрам угла од 30°, а тај угао је степен степена мердевина од земље, то значи да врх мердевина удара у зграду 20 стопа од земље.

палиндромски број

Наш коначни одговор је 20 стопа.

Тригонометрија

Ако је у правоуглом троуглу син Θ = /2$ и најкраћа дужина крака је 8. Колика је дужина странице која недостаје а НИЈЕ хипотенуза?

Пошто знате своја правила 30-60-90, можете решити овај проблем без потребе за питагорином теоремом или калкулатором.

Речено нам је да је ово правоугли троугао, а из наших посебних правила правоуглог троугла знамо да је синус 30° = /2$. Угао који недостаје мора, дакле, бити 60 степени, што ово чини троуглом од 30-60-90.

И пошто је ово троугао 30-60-90, а речено нам је да је најкраћа страница 8, хипотенуза мора бити 16, а страна која недостаје мора бити 8 $ * √3 $, или $ 8√3 $.

Наш коначни одговор је 8√3.

Тхе Таке-Аваис

Сећање на правила за троуглове 30-60-90 ће вам помоћи да пређете кроз различите математичке проблеме . Али имајте на уму да, иако је познавање ових правила згодан алат за држање за појасом, већину проблема и даље можете решити без њих.

Пратите правила $к$, $к√3$, к$ и 30-60-90 на било који начин за вас и покушајте да их држите јаснима ако можете, али немојте паничити ако вам је на уму нестаје када дође време за крч. У сваком случају, имаш ово.

И, ако вам треба више вежбе, само напред и погледајте ово 30-60-90 квиз о троуглу . Срећно полагање теста!