Алгоритам вектора удаљености је итеративан, асинхрони и дистрибуиран.
Дистрибуирано:Дистрибуира се тако што сваки чвор прима информације од једног или више својих директно повезаних суседа, врши прорачун и затим дистрибуира резултат назад својим суседима.Итеративно:Понавља се по томе што се његов процес наставља све док више информација не буде на располагању за размену између суседа.Асинхрони:Не захтева да сви његови чворови раде у кораку закључавања један са другим.
• Алгоритам вектора удаљености је динамички алгоритам.
• Углавном се користи у АРПАНЕТ-у и РИП-у.
• Сваки рутер одржава табелу удаљености познату као Вецтор .

Три кључа за разумевање рада алгоритма рутирања вектора удаљености:

Знање о целој мрежи:Сваки рутер дели своје знање кроз целу мрежу. Рутер шаље своје прикупљено знање о мрежи својим суседима.Рутирање само до суседа:Рутер шаље своје знање о мрежи само оним рутерима који имају директне везе. Рутер шаље све што има о мрежи кроз портове. Рутер прима информације и користи их за ажурирање сопствене табеле рутирања.Размена информација у редовним интервалима:У року од 30 секунди, рутер шаље информације суседним рутерима.

Алгоритам рутирања вектора удаљености

Нека д_Икс(и) бити цена путање са најнижом ценом од чвора к до чвора и. Најмањи трошкови су повезани Беллман-Форд једначином,

 d<sub>x</sub>(y) = min<sub>v</sub>{c(x,v) + d<sub>v</sub>(y)} 

Где минв је једначина узета за све суседе по к. Након путовања од к до в, ако узмемо у обзир пут са најнижом ценом од в до и, цена пута ће бити ц(к,в)+д_ин(и). Најмањи трошак од к до и је минимум ц(к,в)+д_ин(и) преузео све суседе.

Са алгоритмом рутирања вектором удаљености, чвор к садржи следеће информације о рутирању:

• За сваког суседа в, цена ц(к,в) је цена пута од к до директно повезаног суседа, в.
• Вектор удаљености х, тј. Д_Икс= [ Д_Икс(и) : и у Н ], који садржи његову цену до свих одредишта, и, у Н.
• Вектор удаљености сваког од његових суседа, тј., Д_ин= [ Д_ин(и) : и у Н ] за сваког суседа в од к.

Рутирање вектора удаљености је асинхрони алгоритам у коме чвор к шаље копију свог вектора удаљености свим својим суседима. Када чвор к прими нови вектор удаљености од једног од својих суседних вектора, в, он чува вектор удаљености од в и користи Белман-Фордову једначину да ажурира сопствени вектор удаљености. Једначина је дата у наставку:

динамичко програмирање

 d<sub>x</sub>(y) = min<sub>v</sub>{ c(x,v) + d<sub>v</sub>(y)} for each node y in N 

Чвор к је ажурирао своју сопствену табелу вектора удаљености користећи горњу једначину и шаље своју ажурирану табелу свим својим суседима како би могли да ажурирају своје векторе удаљености.

Алгоритам

 At each node x, <p> <strong>Initialization</strong> </p> for all destinations y in N: D<sub>x</sub>(y) = c(x,y) // If y is not a neighbor then c(x,y) = &#x221E; for each neighbor w D<sub>w</sub>(y) = ? for all destination y in N. for each neighbor w send distance vector D<sub>x</sub> = [ D<sub>x</sub>(y) : y in N ] to w <strong>loop</strong> <strong>wait</strong> (until I receive any distance vector from some neighbor w) for each y in N: D<sub>x</sub>(y) = minv{c(x,v)+D<sub>v</sub>(y)} If D<sub>x</sub>(y) is changed for any destination y Send distance vector D<sub>x</sub> = [ D<sub>x</sub>(y) : y in N ] to all neighbors <strong>forever</strong> 

Напомена: У алгоритму вектора удаљености, чвор к ажурира своју табелу када или види било какву промену трошкова у једном директно повезаном чвору или прими било какво ажурирање вектора од неког суседа.

Хајде да разумемо кроз пример:

Дељење информација

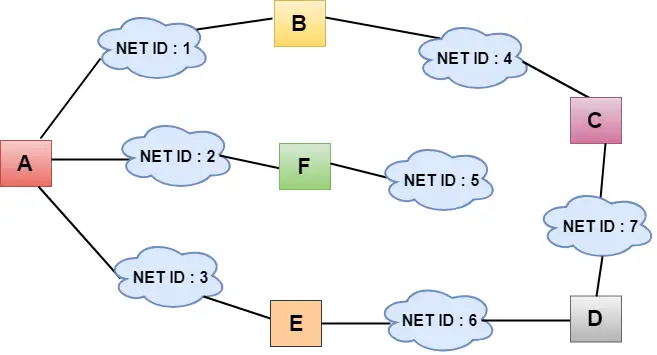
• На горњој слици, сваки облак представља мрежу, а број унутар облака представља ИД мреже.
• Све ЛАН мреже су повезане рутерима, а представљене су у кутијама означеним као А, Б, Ц, Д, Е, Ф.
• Алгоритам рутирања вектора удаљености поједностављује процес рутирања претпостављајући да је цена сваке везе једна јединица. Због тога се ефикасност преноса може мерити бројем веза до одредишта.
• У рутирању вектора удаљености, цена се заснива на броју скокова.

На горњој слици примећујемо да рутер шаље знање непосредним суседима. Комшије додају ово знање свом сопственом знању и шаљу ажурирану табелу својим суседима. На овај начин рутери добијају сопствене информације плус нове информације о суседима.

Табела рутирања

Два процеса се дешавају:

• Креирање табеле
• Ажурирање табеле

Креирање табеле

У почетку, табела рутирања се креира за сваки рутер који садржи најмање три типа информација као што су ИД мреже, цена и следећи скок.

НЕТ ИД:Мрежни ИД дефинише коначно одредиште пакета.Цена:Цена је број скокова који пакет мора да прође да би стигао тамо.Следећи Скок:То је рутер на који се пакет мора испоручити.

• На горњој слици су приказане оригиналне табеле рутирања свих рутера. У табели рутирања, прва колона представља ИД мреже, друга колона представља цену везе, а трећа колона је празна.
• Ове табеле рутирања се шаљу свим суседима.

На пример:

 A sends its routing table to B, F & E. B sends its routing table to A & C. C sends its routing table to B & D. D sends its routing table to E & C. E sends its routing table to A & D. F sends its routing table to A. 

Ажурирање табеле

• Када А прими табелу рутирања од Б, онда користи своје информације да ажурира табелу.
• Табела рутирања Б показује како се пакети могу кретати у мреже 1 и 4.
• Б је сусед рутера А, пакети од А до Б могу стићи у једном скоку. Дакле, 1 се додаје свим трошковима наведеним у табели Б и збир ће бити трошак за достизање одређене мреже.

• Након подешавања, А затим комбинује ову табелу са сопственом табелом да би направио комбиновану табелу.

• Комбинована табела може садржати неке дупле податке. На горњој слици, комбинована табела рутера А садржи дуплиране податке, тако да чува само оне податке који имају најнижу цену. На пример, А може послати податке мрежи 1 на два начина. Први, који не користи следећи рутер, тако да кошта један скок. Други захтева два скока (А до Б, затим Б до мреже 1). Прва опција има најнижу цену, стога се задржава, а друга се одбацује.

• Процес креирања табеле рутирања се наставља за све рутере. Сваки рутер прима информације од суседа и ажурира табелу рутирања.

Коначне табеле рутирања свих рутера су дате у наставку: