Динамичко програмирање је техника која разлаже проблеме у под-проблеме и чува резултат за будуће сврхе тако да не морамо поново да израчунавамо резултат. Подпроблеми су оптимизовани за оптимизацију целокупног решења познатог као својства оптималне подструктуре. Главна употреба динамичког програмирања је решавање проблема оптимизације. Овде проблеми оптимизације значе да када покушавамо да пронађемо минимално или максимално решење проблема. Динамичко програмирање гарантује проналажење оптималног решења проблема ако решење постоји.
Дефиниција динамичког програмирања каже да је то техника за решавање сложеног проблема тако што се прво разбије у колекцију једноставнијих подпроблема, реши сваки подпроблем само једном, а затим сачува њихова решења како би се избегла понављања прорачуна.
Хајде да разумемо овај приступ кроз пример.
Размотримо пример Фибоначијеве серије. Следећи низ је Фибоначијев низ:
шта је авт
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ,…
Бројеви у горњој серији нису насумично израчунати. Математички, могли бисмо да запишемо сваки од појмова користећи следећу формулу:
Ф(н) = Ф(н-1) + Ф(н-2),
Са основним вредностима Ф(0) = 0, и Ф(1) = 1. Да бисмо израчунали остале бројеве, следимо горњи однос. На пример, Ф(2) је збир ф(0) и ф(1), што је једнако 1.
Како можемо израчунати Ф(20)?
Ф(20) члан ће се израчунати коришћењем н-те формуле Фибоначијевог низа. Слика испод показује како се Ф(20) израчунава.
како приступити ицлоуд фотографијама
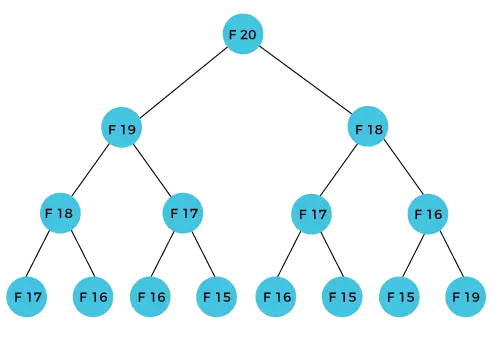
Као што можемо приметити на горњој слици да је Ф(20) израчунат као збир Ф(19) и Ф(18). У приступу динамичког програмирања покушавамо да поделимо проблем на сличне подпроблеме. Овај приступ следимо у горњем случају где је Ф(20) у сличне подпроблеме, тј. Ф(19) и Ф(18). Ако поновимо дефиницију динамичког програмирања, она каже да сличан подпроблем не треба рачунати више од једном. Ипак, у горњем случају, подпроблем се израчунава два пута. У горњем примеру, Ф(18) се израчунава два пута; слично, Ф(17) се такође израчунава два пута. Међутим, ова техника је прилично корисна јер решава сличне подпроблеме, али морамо да будемо опрезни док чувамо резултате јер нисмо посебно заинтересовани за складиштење резултата који смо једном израчунали, онда то може довести до губитка ресурса.
У горњем примеру, ако израчунамо Ф(18) у десном подстаблу, онда то доводи до огромне употребе ресурса и смањује укупне перформансе.
Решење горњег проблема је да сачувате израчунате резултате у низу. Прво израчунавамо Ф(16) и Ф(17) и чувамо њихове вредности у низу. Ф(18) се израчунава сумирањем вредности Ф(17) и Ф(16), које су већ сачуване у низу. Израчуната вредност Ф(18) се чува у низу. Вредност Ф(19) се израчунава коришћењем збира Ф(18) и Ф(17), а њихове вредности су већ сачуване у низу. Израчуната вредност Ф(19) се чува у низу. Вредност Ф(20) се може израчунати додавањем вредности Ф(19) и Ф(18), а вредности и Ф(19) и Ф(18) се чувају у низу. Коначна израчуната вредност Ф(20) се чува у низу.
Како функционише приступ динамичког програмирања?
Следе кораци које следи динамичко програмирање:
- Она разлаже сложени проблем на једноставније подпроблеме.
- Проналази оптимално решење за ове подпроблеме.
- У њему се чувају резултати подпроблема (мемоизација). Процес чувања резултата подпроблема познат је као меморисање.
- Поново их користи тако да се исти подпроблем израчунава више пута.
- На крају, израчунајте резултат сложеног задатка.
Горњих пет корака су основни кораци за динамичко програмирање. Применљиво је динамичко програмирање које има својства као што су:
како претворити цхар у стринг јава
Они проблеми који имају подпроблеме који се преклапају и оптималне подструктуре. Овде оптимална подструктура значи да се решење проблема оптимизације може добити једноставним комбиновањем оптималног решења свих подпроблема.
У случају динамичког програмирања, просторна сложеност би се повећала како чувамо међурезултате, али би се временска сложеност смањила.
Приступи динамичком програмирању
Постоје два приступа динамичком програмирању:
- Одозго на доле приступ
- Приступ одоздо према горе
Одозго на доле приступ
Приступ одозго према доле прати технику памћења, док приступ одоздо према горе прати метод табеле. Овде је меморисање једнако збиру рекурзије и кеширања. Рекурзија значи позивање саме функције, док кеширање значи чување међурезултата.
шта значи кд
Предности
- Веома је лако разумети и применити.
- Решава подпроблеме само када је то потребно.
- Лако је отклонити грешке.
Недостаци
Користи технику рекурзије која заузима више меморије у стеку позива. Понекад када је рекурзија превише дубока, долази до стања преливања стека.
Заузима више меморије што деградира укупне перформансе.
Хајде да разумемо динамичко програмирање кроз пример.
int fib(int n) { if(n<0) error; if(n="=0)" return 0; 1; sum="fib(n-1)" + fib(n-2); } < pre> <p>In the above code, we have used the recursive approach to find out the Fibonacci series. When the value of 'n' increases, the function calls will also increase, and computations will also increase. In this case, the time complexity increases exponentially, and it becomes 2<sup>n</sup>.</p> <p>One solution to this problem is to use the dynamic programming approach. Rather than generating the recursive tree again and again, we can reuse the previously calculated value. If we use the dynamic programming approach, then the time complexity would be O(n).</p> <p>When we apply the dynamic programming approach in the implementation of the Fibonacci series, then the code would look like:</p> <pre> static int count = 0; int fib(int n) { if(memo[n]!= NULL) return memo[n]; count++; if(n<0) error; if(n="=0)" return 0; 1; sum="fib(n-1)" + fib(n-2); memo[n]="sum;" } < pre> <p>In the above code, we have used the memorization technique in which we store the results in an array to reuse the values. This is also known as a top-down approach in which we move from the top and break the problem into sub-problems.</p> <h3>Bottom-Up approach</h3> <p>The bottom-up approach is also one of the techniques which can be used to implement the dynamic programming. It uses the tabulation technique to implement the dynamic programming approach. It solves the same kind of problems but it removes the recursion. If we remove the recursion, there is no stack overflow issue and no overhead of the recursive functions. In this tabulation technique, we solve the problems and store the results in a matrix.</p> <p>There are two ways of applying dynamic programming:</p> <ul> <tr><td>Top-Down</td> </tr><tr><td>Bottom-Up</td> </tr></ul> <p>The bottom-up is the approach used to avoid the recursion, thus saving the memory space. The bottom-up is an algorithm that starts from the beginning, whereas the recursive algorithm starts from the end and works backward. In the bottom-up approach, we start from the base case to find the answer for the end. As we know, the base cases in the Fibonacci series are 0 and 1. Since the bottom approach starts from the base cases, so we will start from 0 and 1.</p> <p> <strong>Key points</strong> </p> <ul> <li>We solve all the smaller sub-problems that will be needed to solve the larger sub-problems then move to the larger problems using smaller sub-problems.</li> <li>We use for loop to iterate over the sub-problems.</li> <li>The bottom-up approach is also known as the tabulation or table filling method.</li> </ul> <p> <strong>Let's understand through an example.</strong> </p> <p>Suppose we have an array that has 0 and 1 values at a[0] and a[1] positions, respectively shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-2.webp" alt="Dynamic Programming"> <p>Since the bottom-up approach starts from the lower values, so the values at a[0] and a[1] are added to find the value of a[2] shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-3.webp" alt="Dynamic Programming"> <p>The value of a[3] will be calculated by adding a[1] and a[2], and it becomes 2 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-4.webp" alt="Dynamic Programming"> <p>The value of a[4] will be calculated by adding a[2] and a[3], and it becomes 3 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-5.webp" alt="Dynamic Programming"> <p>The value of a[5] will be calculated by adding the values of a[4] and a[3], and it becomes 5 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-6.webp" alt="Dynamic Programming"> <p>The code for implementing the Fibonacci series using the bottom-up approach is given below:</p> <pre> int fib(int n) { int A[]; A[0] = 0, A[1] = 1; for( i=2; i<=n; i++) { a[i]="A[i-1]" + a[i-2] } return a[n]; < pre> <p>In the above code, base cases are 0 and 1 and then we have used for loop to find other values of Fibonacci series.</p> <p> <strong>Let's understand through the diagrammatic representation.</strong> </p> <p>Initially, the first two values, i.e., 0 and 1 can be represented as:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-7.webp" alt="Dynamic Programming"> <p>When i=2 then the values 0 and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-8.webp" alt="Dynamic Programming"> <p>When i=3 then the values 1and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-9.webp" alt="Dynamic Programming"> <p>When i=4 then the values 2 and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-10.webp" alt="Dynamic Programming"> <p>When i=5, then the values 3 and 2 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-11.webp" alt="Dynamic Programming"> <p>In the above case, we are starting from the bottom and reaching to the top.</p> <hr></=n;></pre></0)></pre></0)>