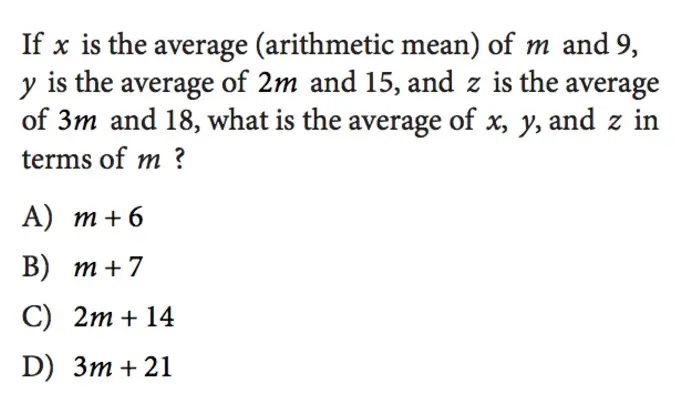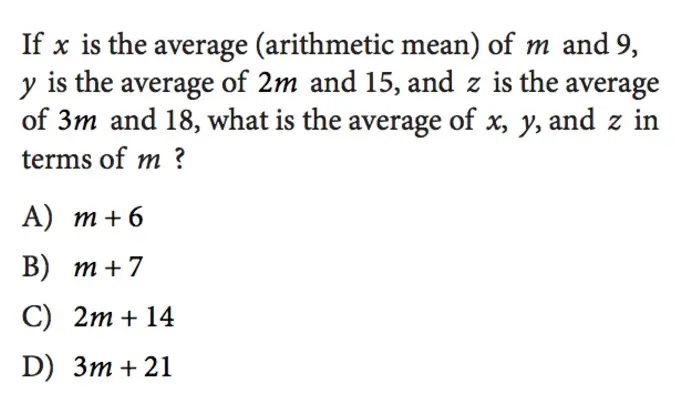Желите да се тестирате против најтежих САТ математичких питања? Желите да знате шта ова питања чини тако тешким и како их најбоље решити? Ако сте спремни да заиста утонете своје зубе у САТ одељак из математике и усредсредите се на савршен резултат, онда је ово водич за вас.
Саставили смо оно што верујемо да јесте 15 најтежих питања за тренутни САТ , са стратегијама и објашњењима одговора за сваки. Ово су све тешка САТ математичка питања са САТ тестова за вежбање Цоллеге Боард-а, што значи да је њихово разумевање један од најбољих начина за учење за оне од вас који теже савршенству.
Слика: Сониа Севилла /Викимедија
Кратак преглед САТ Матх
Трећи и четврти део САТ увек ће бити математички део . Први математички пододељак (означен са '3') ради не омогућавају вам да користите калкулатор, док је други математички пододељак (означен са '4') ради дозволити коришћење калкулатора. Међутим, не брините превише о одељку без калкулатора: ако вам није дозвољено да користите калкулатор за питање, то значи да вам није потребан калкулатор да бисте одговорили на њега.
Сваки математички пододељак је распоређен по растућој тежини (где је дуже потребно да се реши проблем и што мање људи на њега тачно одговори, то је теже). У сваком пододељку, питање 1 ће бити „лако“, а питање 15 ће се сматрати „тешким“. Међутим, растућа потешкоћа се ресетује са лаке на тешку на мрежи.
Дакле, питања са вишеструким избором су распоређена по растућој тежини (питања 1 и 2 ће бити најлакша, питања 14 и 15 ће бити најтежа), али ниво тежине се ресетује за одељак мреже (што значи да ће питања 16 и 17 поново бити 'лако', а питања 19 и 20 ће бити веома тешка).
Уз врло мало изузетака, дакле, најтежи САТ математички задаци ће бити групирани на крају сегмената са вишеструким избором или у другој половини питања у мрежи. Међутим, поред њиховог постављања на тест, ова питања имају и неколико других заједничких карактеристика. За минут ћемо погледати примере питања и како да их решимо, а затим их анализирамо да бисмо открили шта је заједничко овим врстама питања.
Али прво: да ли би требало да се сада фокусирате на најтежа математичка питања?
Ако тек почињете са припремама за учење (или ако сте једноставно прескочили овај први, кључни корак), дефинитивно престаните и урадите потпуни тест да бисте проценили свој тренутни ниво бодова. Погледајте наш водич за сви бесплатни САТ тестови за вежбање доступни на мрежи а затим седите да урадите тест одједном.
Апсолутно најбољи начин да процените свој тренутни ниво је да једноставно урадите САТ тест као да је стваран, држећи стриктно време и радећи директно са само дозвољеним паузама (знамо - вероватно није ваш омиљени начин да проведете суботу). Када стекнете добру представу о свом тренутном нивоу и процентуалном рангирању, можете поставити прекретнице и циљеве за свој коначни резултат САТ математике.
Ако тренутно постижете резултате у распону од 200-400 или 400-600 на САТ математици, најбоље је да прво погледате наш водич за побољшање вашег математичког резултата да стално будете на или преко 600 пре него што почнете да покушавате да се ухватите у коштац са најтежим математичким проблемима на тесту.
Међутим, ако већ постижете више од 600 поена у одељку из математике и желите да тестирате своју снагу за прави САТ, онда свакако пређите на остатак овог водича. Ако тежите савршеном (или близу) , онда ћете морати да знате како изгледају најтежа САТ математичка питања и како да их решите. И на срећу, управо то ћемо и урадити.
УПОЗОРЕЊЕ: Пошто постоји ограничен број званични САТ практични тестови , можда ћете желети да сачекате да прочитате овај чланак док не покушате све или већину прва четири званична теста за вежбање (пошто је већина питања у наставку преузета из тих тестова). Ако сте забринути да не покварите те тестове, престаните сада да читате овај водич; вратите се и прочитајте када их завршите.

Хајде сада да пређемо на нашу листу питања (вхоо)!
Слика: Ниитк /ДевиантАрт
15 најтежих САТ математичких питања
Сада када сте сигурни да би требало да покушате са оваквим питањима, хајде да одмах уђемо! У наставку смо припремили 15 најтежих САТ математичких питања које можете испробати, заједно са упутствима о томе како да добијете одговор (ако сте збуњени).
Нема калкулатора САТ математичких питања
Питање 1
$$Ц=5/9(Ф-32)$$
Горња једначина показује како је температура $Ф$, мерена у степенима Фаренхајта, повезана са температуром $Ц$, мереном у степенима Целзијуса. На основу једначине, шта од следећег мора бити тачно?
- Повећање температуре од 1 степен Фаренхајта је еквивалентно повећању температуре од 5/9$ степени Целзијуса.
- Повећање температуре од 1 степен Целзијуса је еквивалентно повећању температуре од 1,8 степени Фаренхајта.
- Повећање температуре од /9$ степени Фаренхајта је еквивалентно порасту температуре од 1 степен Целзијуса.
А) Само ја
Б) Само ИИ
Ц) Само ИИИ
Д) само И и ИИ
ОБЈАШЊЕЊЕ ОДГОВОРА: Замислите једначину као једначину за праву
$$и=мк+б$$
где у овом случају
$$Ц= {5}/{9} (Ф−32)$$
или
$$Ц={5}/{9}Ф −{5}/{9}(32)$$
Можете да видите да је нагиб графика /{9}$, што значи да је за повећање од 1 степен Фаренхајта повећање износи /{9}$ од 1 степен Целзијуса.
$$Ц= {5}/{9} (Ф)$$
$$Ц= {5}/{9} (1)= {5}/{9}$$
Дакле, изјава И је тачна. Ово је еквивалентно томе да кажемо да је повећање од 1 степен Целзијуса једнако повећању од /{5}$ степени Фаренхајта.
$$Ц= {5}/{9} (Ф)$$
$= {5}/{9} (Ф)$$
$$(Ф)={9}/{5}$$
Пошто је /{5}$ = 1,8, изјава ИИ је тачна.
Једини одговор који има и исказ И и исказ ИИ као тачан је Д , али ако имате времена и желите да будете потпуно темељни, такође можете да проверите да ли је изјава ИИИ (повећање од /{9}$ степен Фаренхајта једнако повећању температуре од 1 степен Целзијуса) тачна :
$$Ц= {5}/{9} (Ф)$$
$$Ц= {5}/{9} ({5}/{9})$$
$$Ц= {25} /{81} (што је = 1)$$
Повећање од /9$ степени Фаренхајта доводи до повећања од /{81}$, а не за 1 степен Целзијуса, тако да изјава ИИИ није тачна.
Коначан одговор је Д.
Питање 2
Једначина${24к^2 + 25к -47}/{ак-2} = -8к-3-{53/{ак-2}}$важи за све вредности $к=2/а$, где је $а$ константа.
Која је вредност $а$?
А) -16
Б) -3
Ц) 3
Д) 16
објекат у јава програмирању
ОБЈАШЊЕЊЕ ОДГОВОРА: Постоје два начина да се ово питање реши. Бржи начин је да помножите сваку страну дате једначине са $ак-2$ (тако да можете да се ослободите разломка). Када помножите сваку страну са $ак-2$, требало би да имате:
$к^2 + 25к - 47 = (-8к-3)(ак-2) - 53$$
Затим би требало да помножите $(-8к-3)$ и $(ак-2)$ користећи ФОИЛ.
$к^2 + 25к - 47 = -8ак^2 - 3ак +16к + 6 - 53$$
Затим смањите на десној страни једначине
$к^2 + 25к - 47 = -8ак^2 - 3ак +16к - 47$$
Пошто коефицијенти $к^2$-члана морају бити једнаки на обе стране једначине, $−8а = 24$, или $а = −3$.
Друга опција која је дужа и досаднија је да покушате да укључите све изборе одговора за а и видите који избор одговора чини обе стране једначине једнакима. Опет, ово је дужа опција и не препоручујем је за стварни САТ јер ће изгубити превише времена.
Коначни одговор је Б.
Питање 3
Ако је к-и = 12$, колика је вредност ${8^к}/{2^и}$?
А) ^{12}$
Б) ^4$
Ц) ^2$
Д) Вредност се не може утврдити из датих информација.
ОБЈАШЊЕЊЕ ОДГОВОРА: Један приступ је изражавање
$${8^к}/{2^и}$$
тако да су бројилац и именилац изражени истом основом. Пошто су 2 и 8 оба степена од 2, замена ^3$ за 8 у бројиоцу од ${8^к}/{2^и}$ даје
$${(2^3)^к}/{2^и}$$
који се може преписати
$${2^3к}/{2^и}$$
Пошто бројилац и именилац имају заједничку основу, овај израз се може преписати као ^(3к−и)$. У питању се наводи да је к − и = 12$, па се експонент, к − и$ може заменити са 12, што значи да
$${8^к}/{2^и}= 2^12$$
Коначан одговор је А.
Питање 4
Тачке А и Б леже на кругу полупречника 1, а лук ${АБ}↖⌢$ има дужину од $π/3$. Колики део обима круга је дужина лука ${АБ}↖⌢$?
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте сазнали одговор на ово питање, прво ћете морати да знате формулу за проналажење обима круга.
Обим, $Ц$, круга је $Ц = 2πр$, где је $р$ полупречник круга. За дати круг полупречника 1, обим је $Ц = 2(π)(1)$, или $Ц = 2π$.
Да бисте сазнали колики је део обима дужине ${АБ}↖⌢$, поделите дужину лука са обимом, што даје $π/3 ÷ 2π$. Ова подела се може представити са $π/3 * {1/2}π = 1/6$.
Разломак /6$ се такође може преписати као 
Желите да се тестирате против најтежих САТ математичких питања? Желите да знате шта ова питања чини тако тешким и како их најбоље решити? Ако сте спремни да заиста утонете своје зубе у САТ одељак из математике и усредсредите се на савршен резултат, онда је ово водич за вас.
Саставили смо оно што верујемо да јесте 15 најтежих питања за тренутни САТ , са стратегијама и објашњењима одговора за сваки. Ово су све тешка САТ математичка питања са САТ тестова за вежбање Цоллеге Боард-а, што значи да је њихово разумевање један од најбољих начина за учење за оне од вас који теже савршенству.
Слика: Сониа Севилла /Викимедија
Кратак преглед САТ Матх
Трећи и четврти део САТ увек ће бити математички део . Први математички пододељак (означен са '3') ради не омогућавају вам да користите калкулатор, док је други математички пододељак (означен са '4') ради дозволити коришћење калкулатора. Међутим, не брините превише о одељку без калкулатора: ако вам није дозвољено да користите калкулатор за питање, то значи да вам није потребан калкулатор да бисте одговорили на њега.
Сваки математички пододељак је распоређен по растућој тежини (где је дуже потребно да се реши проблем и што мање људи на њега тачно одговори, то је теже). У сваком пододељку, питање 1 ће бити „лако“, а питање 15 ће се сматрати „тешким“. Међутим, растућа потешкоћа се ресетује са лаке на тешку на мрежи.
Дакле, питања са вишеструким избором су распоређена по растућој тежини (питања 1 и 2 ће бити најлакша, питања 14 и 15 ће бити најтежа), али ниво тежине се ресетује за одељак мреже (што значи да ће питања 16 и 17 поново бити 'лако', а питања 19 и 20 ће бити веома тешка).
Уз врло мало изузетака, дакле, најтежи САТ математички задаци ће бити групирани на крају сегмената са вишеструким избором или у другој половини питања у мрежи. Међутим, поред њиховог постављања на тест, ова питања имају и неколико других заједничких карактеристика. За минут ћемо погледати примере питања и како да их решимо, а затим их анализирамо да бисмо открили шта је заједничко овим врстама питања.
Али прво: да ли би требало да се сада фокусирате на најтежа математичка питања?
Ако тек почињете са припремама за учење (или ако сте једноставно прескочили овај први, кључни корак), дефинитивно престаните и урадите потпуни тест да бисте проценили свој тренутни ниво бодова. Погледајте наш водич за сви бесплатни САТ тестови за вежбање доступни на мрежи а затим седите да урадите тест одједном.
Апсолутно најбољи начин да процените свој тренутни ниво је да једноставно урадите САТ тест као да је стваран, држећи стриктно време и радећи директно са само дозвољеним паузама (знамо - вероватно није ваш омиљени начин да проведете суботу). Када стекнете добру представу о свом тренутном нивоу и процентуалном рангирању, можете поставити прекретнице и циљеве за свој коначни резултат САТ математике.
Ако тренутно постижете резултате у распону од 200-400 или 400-600 на САТ математици, најбоље је да прво погледате наш водич за побољшање вашег математичког резултата да стално будете на или преко 600 пре него што почнете да покушавате да се ухватите у коштац са најтежим математичким проблемима на тесту.
Међутим, ако већ постижете више од 600 поена у одељку из математике и желите да тестирате своју снагу за прави САТ, онда свакако пређите на остатак овог водича. Ако тежите савршеном (или близу) , онда ћете морати да знате како изгледају најтежа САТ математичка питања и како да их решите. И на срећу, управо то ћемо и урадити.
УПОЗОРЕЊЕ: Пошто постоји ограничен број званични САТ практични тестови , можда ћете желети да сачекате да прочитате овај чланак док не покушате све или већину прва четири званична теста за вежбање (пошто је већина питања у наставку преузета из тих тестова). Ако сте забринути да не покварите те тестове, престаните сада да читате овај водич; вратите се и прочитајте када их завршите.

Хајде сада да пређемо на нашу листу питања (вхоо)!
Слика: Ниитк /ДевиантАрт
15 најтежих САТ математичких питања
Сада када сте сигурни да би требало да покушате са оваквим питањима, хајде да одмах уђемо! У наставку смо припремили 15 најтежих САТ математичких питања које можете испробати, заједно са упутствима о томе како да добијете одговор (ако сте збуњени).
Нема калкулатора САТ математичких питања
Питање 1
$$Ц=5/9(Ф-32)$$
Горња једначина показује како је температура $Ф$, мерена у степенима Фаренхајта, повезана са температуром $Ц$, мереном у степенима Целзијуса. На основу једначине, шта од следећег мора бити тачно?
- Повећање температуре од 1 степен Фаренхајта је еквивалентно повећању температуре од 5/9$ степени Целзијуса.
- Повећање температуре од 1 степен Целзијуса је еквивалентно повећању температуре од 1,8 степени Фаренхајта.
- Повећање температуре од $5/9$ степени Фаренхајта је еквивалентно порасту температуре од 1 степен Целзијуса.
А) Само ја
Б) Само ИИ
Ц) Само ИИИ
Д) само И и ИИ
ОБЈАШЊЕЊЕ ОДГОВОРА: Замислите једначину као једначину за праву
$$и=мк+б$$
где у овом случају
$$Ц= {5}/{9} (Ф−32)$$
или
$$Ц={5}/{9}Ф −{5}/{9}(32)$$
Можете да видите да је нагиб графика ${5}/{9}$, што значи да је за повећање од 1 степен Фаренхајта повећање износи ${5}/{9}$ од 1 степен Целзијуса.
$$Ц= {5}/{9} (Ф)$$
$$Ц= {5}/{9} (1)= {5}/{9}$$
Дакле, изјава И је тачна. Ово је еквивалентно томе да кажемо да је повећање од 1 степен Целзијуса једнако повећању од ${9}/{5}$ степени Фаренхајта.
$$Ц= {5}/{9} (Ф)$$
$$1= {5}/{9} (Ф)$$
$$(Ф)={9}/{5}$$
Пошто је ${9}/{5}$ = 1,8, изјава ИИ је тачна.
Једини одговор који има и исказ И и исказ ИИ као тачан је Д , али ако имате времена и желите да будете потпуно темељни, такође можете да проверите да ли је изјава ИИИ (повећање од ${5}/{9}$ степен Фаренхајта једнако повећању температуре од 1 степен Целзијуса) тачна :
$$Ц= {5}/{9} (Ф)$$
$$Ц= {5}/{9} ({5}/{9})$$
$$Ц= {25} /{81} (што је = 1)$$
Повећање од $5/9$ степени Фаренхајта доводи до повећања од ${25}/{81}$, а не за 1 степен Целзијуса, тако да изјава ИИИ није тачна.
Коначан одговор је Д.
Питање 2
Једначина${24к^2 + 25к -47}/{ак-2} = -8к-3-{53/{ак-2}}$важи за све вредности $к=2/а$, где је $а$ константа.
Која је вредност $а$?
А) -16
Б) -3
Ц) 3
Д) 16
ОБЈАШЊЕЊЕ ОДГОВОРА: Постоје два начина да се ово питање реши. Бржи начин је да помножите сваку страну дате једначине са $ак-2$ (тако да можете да се ослободите разломка). Када помножите сваку страну са $ак-2$, требало би да имате:
$$24к^2 + 25к - 47 = (-8к-3)(ак-2) - 53$$
Затим би требало да помножите $(-8к-3)$ и $(ак-2)$ користећи ФОИЛ.
$$24к^2 + 25к - 47 = -8ак^2 - 3ак +16к + 6 - 53$$
Затим смањите на десној страни једначине
$$24к^2 + 25к - 47 = -8ак^2 - 3ак +16к - 47$$
Пошто коефицијенти $к^2$-члана морају бити једнаки на обе стране једначине, $−8а = 24$, или $а = −3$.
Друга опција која је дужа и досаднија је да покушате да укључите све изборе одговора за а и видите који избор одговора чини обе стране једначине једнакима. Опет, ово је дужа опција и не препоручујем је за стварни САТ јер ће изгубити превише времена.
Коначни одговор је Б.
Питање 3
Ако је $3к-и = 12$, колика је вредност ${8^к}/{2^и}$?
А) $2^{12}$
Б) $4^4$
Ц) $8^2$
Д) Вредност се не може утврдити из датих информација.
ОБЈАШЊЕЊЕ ОДГОВОРА: Један приступ је изражавање
$${8^к}/{2^и}$$
тако да су бројилац и именилац изражени истом основом. Пошто су 2 и 8 оба степена од 2, замена $2^3$ за 8 у бројиоцу од ${8^к}/{2^и}$ даје
$${(2^3)^к}/{2^и}$$
који се може преписати
$${2^3к}/{2^и}$$
Пошто бројилац и именилац имају заједничку основу, овај израз се може преписати као $2^(3к−и)$. У питању се наводи да је $3к − и = 12$, па се експонент, $3к − и$ може заменити са 12, што значи да
$${8^к}/{2^и}= 2^12$$
Коначан одговор је А.
Питање 4
Тачке А и Б леже на кругу полупречника 1, а лук ${АБ}↖⌢$ има дужину од $π/3$. Колики део обима круга је дужина лука ${АБ}↖⌢$?
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте сазнали одговор на ово питање, прво ћете морати да знате формулу за проналажење обима круга.
Обим, $Ц$, круга је $Ц = 2πр$, где је $р$ полупречник круга. За дати круг полупречника 1, обим је $Ц = 2(π)(1)$, или $Ц = 2π$.
Да бисте сазнали колики је део обима дужине ${АБ}↖⌢$, поделите дужину лука са обимом, што даје $π/3 ÷ 2π$. Ова подела се може представити са $π/3 * {1/2}π = 1/6$.
Разломак $1/6$ се такође може преписати као $0,166$ или $0,167$.
Коначни одговор је $1/6$, $0,166$ или $0,167$.
Питање 5
$${8-и}/{3-2и}$$
Ако се горњи израз препише у облику $а+би$, где су $а$ и $б$ реални бројеви, колика је вредност $а$? (Напомена: $и=√{-1}$)
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте преписали ${8-и}/{3-2и}$ у стандардном облику $а + би$, потребно је да помножите бројилац и именилац од ${8-и}/{3-2и}$ коњугатом , $3 + 2и$. Ово је једнако
$$({8-и}/{3-2и})({3+2и}/{3+2и})={24+16и-3+(-и)(2и)}/{(3^2 )-(2и)^2}$$
Пошто $и^2=-1$, овај последњи разломак се може поједноставити на
$$ {24+16и-3и+2}/{9-(-4)}={26+13и}/{13}$$
што даље поједностављује на $2 + и$. Стога, када се ${8-и}/{3-2и}$ поново напише у стандардном облику а + би, вредност а је 2.
Коначан одговор је А.
Питање 6
У троуглу $АБЦ$, мера $∠Б$ је 90°, $БЦ=16$ и $АЦ$=20. Троугао $ДЕФ$ је сличан троуглу $АБЦ$, где врхови $Д$, $Е$ и $Ф$ одговарају теменима $А$, $Б$ и $Ц$, респективно, и свакој страни троугла $ ДЕФ$ је $1/3$ дужина одговарајуће странице троугла $АБЦ$. Која је вредност $синФ$?
ОБЈАШЊЕЊЕ ОДГОВОРА: Троугао АБЦ је правоугли троугао са правим углом у Б. Према томе, $ов {АЦ}$ је хипотенуза правоуглог троугла АБЦ, а $ов {АБ}$ и $ов {БЦ}$ су катете правоугли троугао АБЦ. Према Питагориној теореми,
$$АБ =√{20^2-16^2}=√{400-256}=√{144}=12$$
Пошто је троугао ДЕФ сличан троуглу АБЦ, са врхом Ф који одговара темену Ц, мера $угла ∠ {Ф}$ једнака је мери $угла ∠ {Ц}$. Дакле, $син Ф = син Ц$. Од дужина страница троугла АБЦ,
$$синФ ={супротно сиде}/{хипотенусе}={АБ}/{АЦ}={12}/{20}={3}/{5}$$
Дакле, $синФ ={3}/{5}$.
Коначни одговор је ${3}/{5}$ или 0,6.
Питања из математике за САТ дозвољена за калкулатор
Питање 7

Непотпуна табела изнад сумира број ученика леворуких и десноруких ученика према полу за ученике осмог разреда средње школе Кеисел. Десноруких ученица има 5 пута више него леворуких, а 9 пута више дешњака него леворуких ученика. ако у школи има укупно 18 леворуких ученика и 122 дешњака, шта је од следећег најближе вероватноћи да је случајно одабран дешњак женског пола? (Напомена: Претпоставимо да ниједан ученик осмог разреда није и дешњак и леворук.)
А) 0,410
Б) 0,357
Ц) 0,333
Д) 0,250
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте решили овај проблем, требало би да направите две једначине користећи две променљиве ($к$ и $и$) и информације које сте добили. Нека је $к$ број леворуких ученица и нека је $и$ број леворуких ученика. Користећи информације дате у задатку, број дешњака ће бити $5к$, а број дешњака ће бити $9и$. Пошто је укупан број леворуких ученика 18, а укупан број дешњака 122, систем једначина испод мора да буде тачан:
$$к + и = 18$$
$$5к + 9и = 122$$
Када решите овај систем једначина, добијате $к = 10$ и $и = 8$. Дакле, 5*10, односно 50, од 122 дешњака су жене. Према томе, вероватноћа да је дешњак изабран насумично женско је ${50}/{122}$, што је на најближи хиљадити део 0,410.
Коначан одговор је А.Питања 8 и 9
Користите следеће информације и за питање 7 и за питање 8.
Ако купци уђу у продавницу просечном брзином од $р$ купаца по минуту и сваки остане у продавници просечно време од $Т$ минута, даје се просечан број купаца у продавници, $Н$, у било ком тренутку по формули $Н=рТ$. Овај однос је познат као Литлов закон.
Власник Гоод Деалс Сторе-а процењује да током радног времена у продавницу уђу у просеку 3 купца у минуту и да се сваки од њих задржава у просеку 15 минута. Власник продавнице користи Литлов закон да процени да у продавници у сваком тренутку има 45 купаца.
Питање 8
Литтлеов закон се може применити на било који део продавнице, као што је одређено одељење или редови на благајни. Власник продавнице утврђује да током радног времена отприлике 84 купца по сату обави куповину и сваки од ових купаца проведе у просеку 5 минута на каси. У било ком тренутку током радног времена, колико отприлике купаца у просеку чека у реду за касу да обави куповину у продавници Гоод Деалс?
ОБЈАШЊЕЊЕ ОДГОВОРА: Пошто питање каже да се Литлов закон може применити на било који део продавнице (на пример, само на ред за одјаву), онда је просечан број купаца, $Н$, у реду за одјаву у било ком тренутку $Н = рТ $, где је $р$ број купаца који улазе у ред за одјаву по минуту, а $Т$ је просечан број минута које сваки купац проведе у реду за плаћање.
Пошто 84 купца на сат обави куповину, 84 купца по сату улази у ред за одјаву. Међутим, ово треба да се конвертује у број купаца у минути (да би се користило са $Т = 5$). Пошто у једном сату има 60 минута, цена је {84 $ купаца по сату}/{60 минута} = 1,4$ купаца по минуту. Коришћење дате формуле са $р = 1.4$ и $Т = 5$ даје принос
$$Н = рт = (1.4)(5) = 7$$
Према томе, просечан број купаца, $Н$, у реду за касу у било ком тренутку током радног времена је 7.
Коначан одговор је 7.
Питање 9
Власник продавнице Гоод Деалс отвара нову продавницу широм града. За нову радњу, власник процењује да ће током радног времена у просеку бити око 90 купаца посатуђу у продавницу и сваки од њих остаје у просеку 12 минута. Просечан број купаца у новој продавници у било ком тренутку је који проценат мањи од просечног броја купаца у оригиналној продавници у било ком тренутку? (Напомена: Занемарите симбол за проценат када уносите свој одговор. На пример, ако је одговор 42,1%, унесите 42,1)
ОБЈАШЊЕЊЕ ОДГОВОРА: Према првобитним информацијама, процењени просечан број купаца у првобитној продавници у било ком тренутку (Н) је 45. У питању се наводи да у новој продавници менаџер процењује да је просечно 90 купаца на сат (60 минута) уђите у продавницу, што је еквивалентно 1,5 купаца у минути (р). Менаџер такође процењује да сваки купац остаје у продавници у просеку 12 минута (Т). Дакле, према Литловом закону, у новој продавници у било ком тренутку има, у просеку, $Н = рТ = (1,5)(12) = 18$ купаца. Ово је
$${45-18}/{45} * 100 = 60$$
проценат мање од просечног броја купаца у оригиналној продавници у било ком тренутку.
Коначан одговор је 60.
Питање 10
У $ки$-равни, тачка $(п,р)$ лежи на правој са једначином $и=к+б$, где је $б$ константа. Тачка са координатама $(2п, 5р)$ лежи на правој са једначином $и=2к+б$. Ако је $п=0$, колика је вредност $р/п$?
А) $2/5$
Б) $3/4$
Ц) $4/3$
Д) $5/2$
ОБЈАШЊЕЊЕ ОДГОВОРА: Пошто тачка $(п,р)$ лежи на правој са једначином $и=к+б$, та тачка мора да задовољи једначину. Замена $п$ за $к$ и $р$ за $и$ у једначини $и=к+б$ даје $р=п+б$, или $би б$ = $би р-би п $.
Слично томе, пошто тачка $(2п,5р)$ лежи на правој са једначином $и=2к+б$, тачка мора да задовољава једначину. Замена $2п$ за $к$ и $5р$ за $и$ у једначини $и=2к+б$ даје:
$5р=2(2п)+б$
$5р=4п+б$
$би б$ = $бо 5 би р-бо 4би п$.
Затим, можемо поставити две једначине једнаке $б$ једна другој и поједноставити:
$б=р-п=5р-4п$
$3п=4р$
Коначно, да бисмо пронашли $р/п$, морамо да поделимо обе стране једначине са $п$ и са $4$:
$3п=4р$
$3={4р}/п$
$3/4=р/п$
Тачан одговор је Б , $3/4$.
Ако сте изабрали изборе А и Д, можда сте погрешно формирали свој одговор од коефицијената у тачки $(2п, 5р)$. Ако сте изабрали избор Ц, можда сте побркали $р$ и $п$.
Имајте на уму да док се ово налази у одељку за калкулатор САТ-а, апсолутно вам није потребан ваш калкулатор да бисте га решили!
Питање 11
 Силос за жито је изграђен од два десна кружна конуса и десног кружног цилиндра са унутрашњим мерама приказаним на слици изнад. Од следећег, који је најближи запремини силоса за зрно, у кубним стопама?
Силос за жито је изграђен од два десна кружна конуса и десног кружног цилиндра са унутрашњим мерама приказаним на слици изнад. Од следећег, који је најближи запремини силоса за зрно, у кубним стопама?
А) 261,8
Б) 785,4
Ц) 916.3
Д) 1047.2
ОБЈАШЊЕЊЕ ОДГОВОРА: Запремина силоса за зрно може се наћи додавањем запремина свих чврстих материја од којих се састоји (цилиндра и два конуса). Силос се састоји од цилиндра (висине 10 стопа и полупречника основе 5 стопа) и два конуса (сваки са висином 5 стопа и полупречником основе 5 стопа). Формуле дате на почетку одељка САТ математике:
Запремина конуса
$$В={1}/{3}πр^2х$$
Запремина цилиндра
$$В=πр^2х$$
може се користити за одређивање укупне запремине силоса. Пошто два конуса имају идентичне димензије, укупна запремина силоса, у кубним стопама, дата је као
$$В_{сило}=π(5^2)(10)+(2)({1}/{3})π(5^2)(5)=({4}/{3})(250 )п$$
што је приближно једнако 1.047,2 кубних стопа.
Коначан одговор је Д.
Питање 12
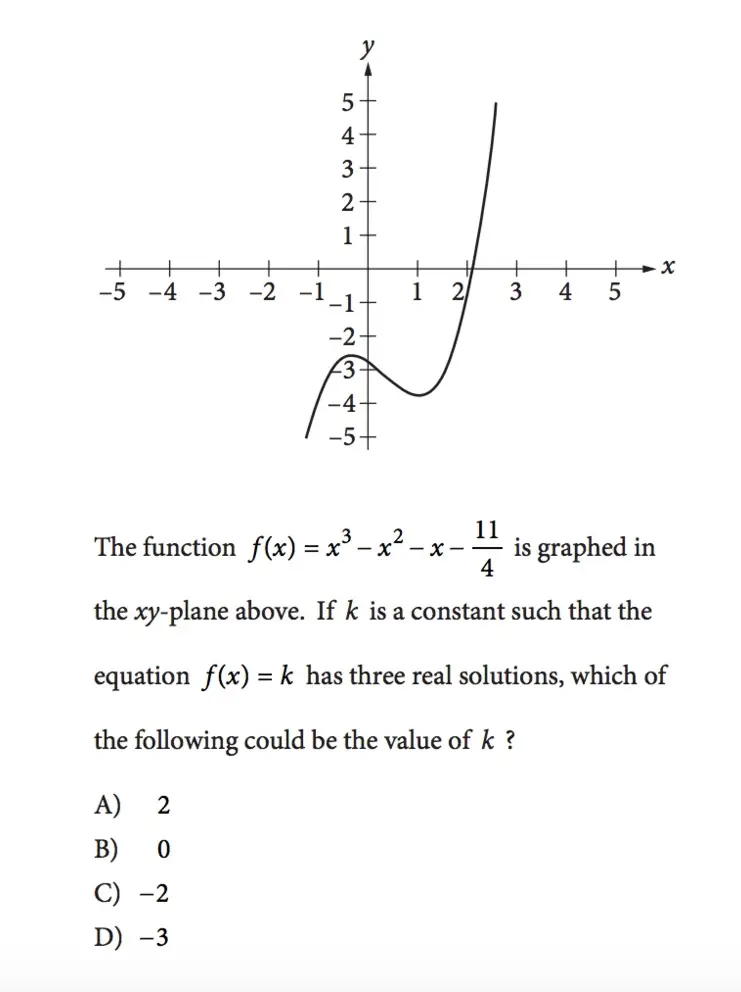
Ако је $к$ просек (аритметичка средина) од $м$ и $9$, $и$ је просек од $2м$ и $15$, а $з$ је просек од $3м$ и $18$, шта је просек од $к$, $и$ и $з$ у смислу $м$?
А) $м+6$
Б) $м+7$
Ц) 2 милиона долара + 14 долара
Д) 3 милиона долара + 21 долара
ОБЈАШЊЕЊЕ ОДГОВОРА: Пошто је просек (аритметичка средина) два броја једнак збиру два броја подељен са 2, једначине $к={м+9}/{2}$, $и={2м+15}/{2 }$, $з={3м+18}/{2}$ су тачне. Просек за $к$, $и$ и $з$ је дат са ${к + и + з}/{3}$. Замена израза у м за сваку променљиву ($к$, $и$, $з$) даје
$$[{м+9}/{2}+{2м+15}/{2}+{3м+18}/{2}]/3$$
Овај разломак се може поједноставити на $м + 7$.
Коначни одговор је Б.
Питање 13
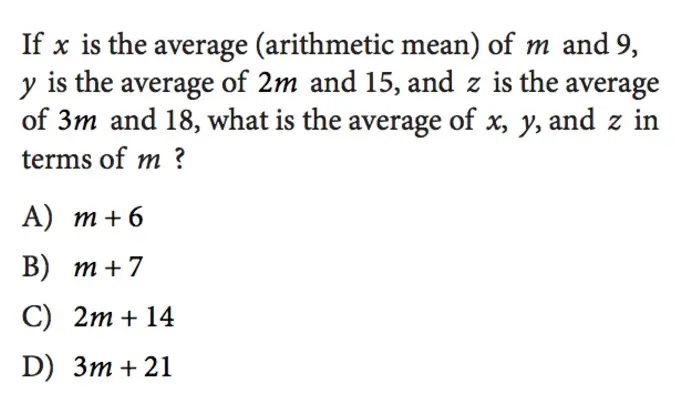
Функција $ф(к)=к^3-к^2-к-{11/4}$ је графички приказана у горњој $ки$-равни. Ако је $к$ константа таква да једначина $ф(к)=к$ има три реална решења, које од следећег може бити вредност $к$?
ОБЈАШЊЕЊЕ ОДГОВОРА: Једначина $ф(к) = к$ даје решења система једначина
$$и = ф(к) = к^3-к^2-к-{11}/{4}$$
и
$$и = к$$
Реално решење система две једначине одговара тачки пресека графика двеју једначина у $ки$-равни.
График $и = к$ је хоризонтална линија која садржи тачку $(0, к)$ и три пута сече график кубичне једначине (пошто има три реална решења). С обзиром на график, једина хоризонтална линија која би три пута пресекла кубну једначину је линија са једначином $и = −3$, или $ф(к) = −3$. Дакле, $к$ је $-3$.
Коначан одговор је Д.
Питање 14
$$к={1/2}нв^2$$
Динамички притисак $к$ генерисан флуидом који се креће брзином $в$ може се наћи коришћењем формуле изнад, где је $н$ константна густина течности. Аеронаутички инжењер користи формулу да пронађе динамички притисак флуида који се креће брзином $в$ и исте течности која се креће брзином 1,5$в$. Колики је однос динамичког притиска бржег флуида и динамичког притиска спорије течности?
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте решили овај проблем, потребно је да поставите једначине са променљивим. Нека је $к_1$ динамички притисак спорије течности која се креће брзином $в_1$, а нека је $к_2$ динамички притисак брже течности која се креће брзином $в_2$. Онда
$$в_2 =1,5в_1$$
Узимајући у обзир једначину $к = {1}/{2}нв^2$, замена динамичког притиска и брзине бржег флуида даје $к_2 = {1}/{2}н(в_2)^2$. Пошто је $в_2 =1.5в_1$, израз $1.5в_1$ може бити замењен са $в_2$ у овој једначини, дајући $к_2 = {1}/{2}н(1.5в_1)^2$. Узимајући на квадрат $1,5$, можете преписати претходну једначину као
$$к_2 = (2.25)({1}/{2})н(в_1)^2 = (2.25)к_1$$
Дакле, однос динамичког притиска бржег флуида је
$${к2}/{к1} = {2,25 к_1}/{к_1}= 2,25 $$
Коначан одговор је 2,25 или 9/4.
Питање 15
За полином $п(к)$, вредност $п(3)$ је $-2$. Шта од следећег мора бити тачно за $п(к)$?
А) $к-5$ је фактор од $п(к)$.
Б) $к-2$ је фактор од $п(к)$.
Ц) $к+2$ је фактор од $п(к)$.
Д) Остатак када се $п(к)$ подели са $к-3$ је $-2$.
ОБЈАШЊЕЊЕ ОДГОВОРА: Ако је полином $п(к)$ подељен полиномом облика $к+к$ (који обухвата све могуће изборе одговора у овом питању), резултат се може написати као
$${п(к)}/{к+к}=к(к)+{р}/{к+к}$$
где је $к(к)$ полином, а $р$ остатак. Пошто је $к + к$ полином степена 1 (што значи да укључује само $к^1$ и нема виших експонента), остатак је реалан број.
Према томе, $п(к)$ се може преписати као $п(к) = (к + к)к(к) + р$, где је $р$ реалан број.
Питање гласи да је $п(3) = -2$, тако да мора бити тачно да
$$-2 = п(3) = (3 + к)к(3) + р$$
Сада можемо укључити све могуће одговоре. Ако је одговор А, Б или Ц, $р$ ће бити $0$, док ако је одговор Д, $р$ ће бити $-2$.
А. $-2 = п(3) = (3 + (-5))к(3) + 0$
$-2=(3-5)к(3)$
$-2=(-2)к(3)$
Ово би могло бити тачно, али само ако је $к(3)=1$
Б. $-2 = п(3) = (3 + (-2))к(3) + 0$
$-2 = (3-2)к(3)$
$-2 = (-1)к(3)$
Ово би могло бити тачно, али само ако је $к(3)=2$
Ц. $-2 = п(3) = (3 + 2)к(3) + 0$
$-2 = (5)к(3)$
Ово би могло бити тачно, али само ако је $к(3)={-2}/{5}$
Д. $-2 = п(3) = (3 + (-3))к(3) + (-2)$
$-2 = (3 - 3)к(3) + (-2)$
$-2 = (0)к(3) + (-2)$
Ово ће увек буди истинит без обзира шта је $к(3)$.
Од избора одговора, једини који мора ако је тачно да је $п(к)$ Д, да је остатак када се $п(к)$ подели са $к-3$ -2.
Коначан одговор је Д.

Заслужујеш све дремке након што прођеш кроз та питања.
Шта је заједничко најтежим САТ математичким питањима?
Важно је разумети шта ова тешка питања чини „тешким“. На тај начин ћете моћи да разумете и решите слична питања када их видите на дан тестирања, као и да имате бољу стратегију за идентификацију и исправљање ваших претходних САТ математичких грешака.
У овом одељку ћемо погледати шта ова питања имају заједничко и дати примере сваке врсте. Неки од разлога зашто су најтежа математичка питања најтежа математичка питања су:
#1: Тестирајте неколико математичких концепата одједном

Овде морамо да се бавимо замишљеним бројевима и разломцима одједном.
Тајна успеха: Размислите коју применљиву математику можете користити да решите проблем, радите корак по корак и испробајте сваку технику док не пронађете ону која функционише!
#2: Укључује много корака
Запамтите: што више корака треба да предузмете, лакше ћете забрљати негде на линији!
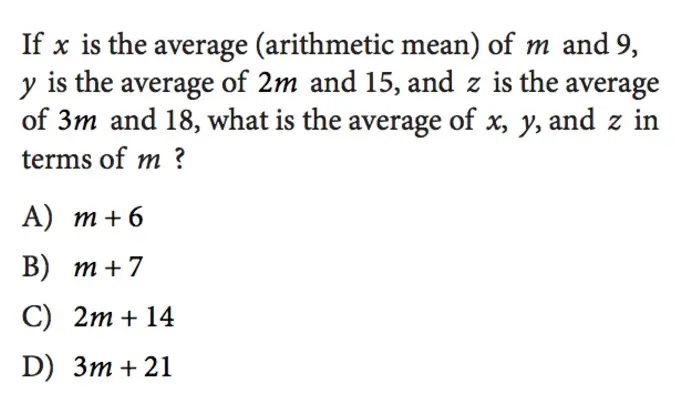
Морамо да решимо овај проблем у корацима (радећи неколико просека) да бисмо откључали остатак одговора у домино ефекту. Ово може бити збуњујуће, посебно ако сте под стресом или вам понестаје времена.
Тајна успеха: Полако, идите корак по корак и још једном проверите свој рад како не бисте погрешили!
#3: Тестирајте концепте са којима сте ограничено упознати
На пример, многи ученици су мање упознати са функцијама него са разломцима и процентима, тако да се већина функционалних питања сматра проблемима „високе тежине“.
Ако не знате како се сналазите у функцијама, ово би био тежак проблем.
Тајна успеха: Прегледајте математичке концепте са којима нисте толико упознати, као што су функције. Предлажемо да користите наше сјајне бесплатне САТ Матх водиче за преглед.
#4: Написане су на необичне или замршене начине
Може бити тешко схватити која су тачно нека питања питајући , а још мање схватити како их решити. Ово је посебно тачно када се питање налази на крају одељка, а понестаје вам времена.

Пошто ово питање пружа толико информација без дијаграма, може бити тешко загонетнути у ограниченом дозвољеном времену.
Тајна успеха: Узмите си времена, анализирајте шта се од вас тражи и нацртајте дијаграм ако вам је од помоћи.
#5: Користите много различитих варијабли

Са толико различитих варијабли у игри, прилично је лако доћи до забуне.
Тајна успеха: Узмите си времена, анализирајте шта се од вас тражи и размислите да ли је додавање бројева добра стратегија за решавање проблема (то не би било за горње питање, али би било за многа друга питања о променљивој САТ).
Тхе Таке-Аваис
САТ је маратон и што сте боље припремљени за њега, боље ћете се осећати на дан тестирања. Ако знате како да се носите са најтежим питањима која вам тест може поставити, чиниће полагање правог САТ-а много мање застрашујућим.
Ако сте сматрали да су ова питања лака, пазите да не потцењујете ефекат адреналина и умора на вашу способност решавања проблема. Док настављате да учите, увек се придржавајте одговарајућих смерница за време и покушајте да урадите пуне тестове кад год је то могуће. Ово је најбољи начин да поново креирате стварно окружење за тестирање како бисте се могли припремити за прави посао.
Ако сматрате да су ова питања изазовна, обавезно ојачајте своје знање математике тако што ћете погледати наше индивидуалне математичке водиче за САТ. Тамо ћете видети детаљнија објашњења тема о којима је реч, као и детаљније рашчлањивање одговора.
Шта је следеће?
Осетили сте да су ова питања тежа него што сте очекивали? Погледајте све теме обухваћене у САТ одељку из математике, а затим забележите који одељци су вам представљали посебну потешкоћу. Затим погледајте наше индивидуалне математичке водиче који ће вам помоћи да учврстите било коју од тих слабих области.
Понестаје вам времена за САТ математичку секцију? Наш водич ће вам помоћи да победите сат и повећате свој резултат.
Циљате на савршен резултат? Провери наш водич о томе како да добијете савршених 800 на САТ одељку из математике , који је написао савршени стрелац.
,166$ или

Желите да се тестирате против најтежих САТ математичких питања? Желите да знате шта ова питања чини тако тешким и како их најбоље решити? Ако сте спремни да заиста утонете своје зубе у САТ одељак из математике и усредсредите се на савршен резултат, онда је ово водич за вас.
Саставили смо оно што верујемо да јесте 15 најтежих питања за тренутни САТ , са стратегијама и објашњењима одговора за сваки. Ово су све тешка САТ математичка питања са САТ тестова за вежбање Цоллеге Боард-а, што значи да је њихово разумевање један од најбољих начина за учење за оне од вас који теже савршенству.
Слика: Сониа Севилла /Викимедија
Кратак преглед САТ Матх
Трећи и четврти део САТ увек ће бити математички део . Први математички пододељак (означен са '3') ради не омогућавају вам да користите калкулатор, док је други математички пододељак (означен са '4') ради дозволити коришћење калкулатора. Међутим, не брините превише о одељку без калкулатора: ако вам није дозвољено да користите калкулатор за питање, то значи да вам није потребан калкулатор да бисте одговорили на њега.
Сваки математички пододељак је распоређен по растућој тежини (где је дуже потребно да се реши проблем и што мање људи на њега тачно одговори, то је теже). У сваком пододељку, питање 1 ће бити „лако“, а питање 15 ће се сматрати „тешким“. Међутим, растућа потешкоћа се ресетује са лаке на тешку на мрежи.
Дакле, питања са вишеструким избором су распоређена по растућој тежини (питања 1 и 2 ће бити најлакша, питања 14 и 15 ће бити најтежа), али ниво тежине се ресетује за одељак мреже (што значи да ће питања 16 и 17 поново бити 'лако', а питања 19 и 20 ће бити веома тешка).
Уз врло мало изузетака, дакле, најтежи САТ математички задаци ће бити групирани на крају сегмената са вишеструким избором или у другој половини питања у мрежи. Међутим, поред њиховог постављања на тест, ова питања имају и неколико других заједничких карактеристика. За минут ћемо погледати примере питања и како да их решимо, а затим их анализирамо да бисмо открили шта је заједничко овим врстама питања.
Али прво: да ли би требало да се сада фокусирате на најтежа математичка питања?
Ако тек почињете са припремама за учење (или ако сте једноставно прескочили овај први, кључни корак), дефинитивно престаните и урадите потпуни тест да бисте проценили свој тренутни ниво бодова. Погледајте наш водич за сви бесплатни САТ тестови за вежбање доступни на мрежи а затим седите да урадите тест одједном.
Апсолутно најбољи начин да процените свој тренутни ниво је да једноставно урадите САТ тест као да је стваран, држећи стриктно време и радећи директно са само дозвољеним паузама (знамо - вероватно није ваш омиљени начин да проведете суботу). Када стекнете добру представу о свом тренутном нивоу и процентуалном рангирању, можете поставити прекретнице и циљеве за свој коначни резултат САТ математике.
Ако тренутно постижете резултате у распону од 200-400 или 400-600 на САТ математици, најбоље је да прво погледате наш водич за побољшање вашег математичког резултата да стално будете на или преко 600 пре него што почнете да покушавате да се ухватите у коштац са најтежим математичким проблемима на тесту.
Међутим, ако већ постижете више од 600 поена у одељку из математике и желите да тестирате своју снагу за прави САТ, онда свакако пређите на остатак овог водича. Ако тежите савршеном (или близу) , онда ћете морати да знате како изгледају најтежа САТ математичка питања и како да их решите. И на срећу, управо то ћемо и урадити.
УПОЗОРЕЊЕ: Пошто постоји ограничен број званични САТ практични тестови , можда ћете желети да сачекате да прочитате овај чланак док не покушате све или већину прва четири званична теста за вежбање (пошто је већина питања у наставку преузета из тих тестова). Ако сте забринути да не покварите те тестове, престаните сада да читате овај водич; вратите се и прочитајте када их завршите.

Хајде сада да пређемо на нашу листу питања (вхоо)!
Слика: Ниитк /ДевиантАрт
15 најтежих САТ математичких питања
Сада када сте сигурни да би требало да покушате са оваквим питањима, хајде да одмах уђемо! У наставку смо припремили 15 најтежих САТ математичких питања које можете испробати, заједно са упутствима о томе како да добијете одговор (ако сте збуњени).
Нема калкулатора САТ математичких питања
Питање 1
$$Ц=5/9(Ф-32)$$
Горња једначина показује како је температура $Ф$, мерена у степенима Фаренхајта, повезана са температуром $Ц$, мереном у степенима Целзијуса. На основу једначине, шта од следећег мора бити тачно?
- Повећање температуре од 1 степен Фаренхајта је еквивалентно повећању температуре од 5/9$ степени Целзијуса.
- Повећање температуре од 1 степен Целзијуса је еквивалентно повећању температуре од 1,8 степени Фаренхајта.
- Повећање температуре од $5/9$ степени Фаренхајта је еквивалентно порасту температуре од 1 степен Целзијуса.
А) Само ја
Б) Само ИИ
Ц) Само ИИИ
Д) само И и ИИ
ОБЈАШЊЕЊЕ ОДГОВОРА: Замислите једначину као једначину за праву
$$и=мк+б$$
где у овом случају
$$Ц= {5}/{9} (Ф−32)$$
или
$$Ц={5}/{9}Ф −{5}/{9}(32)$$
Можете да видите да је нагиб графика ${5}/{9}$, што значи да је за повећање од 1 степен Фаренхајта повећање износи ${5}/{9}$ од 1 степен Целзијуса.
$$Ц= {5}/{9} (Ф)$$
$$Ц= {5}/{9} (1)= {5}/{9}$$
Дакле, изјава И је тачна. Ово је еквивалентно томе да кажемо да је повећање од 1 степен Целзијуса једнако повећању од ${9}/{5}$ степени Фаренхајта.
$$Ц= {5}/{9} (Ф)$$
$$1= {5}/{9} (Ф)$$
$$(Ф)={9}/{5}$$
Пошто је ${9}/{5}$ = 1,8, изјава ИИ је тачна.
Једини одговор који има и исказ И и исказ ИИ као тачан је Д , али ако имате времена и желите да будете потпуно темељни, такође можете да проверите да ли је изјава ИИИ (повећање од ${5}/{9}$ степен Фаренхајта једнако повећању температуре од 1 степен Целзијуса) тачна :
$$Ц= {5}/{9} (Ф)$$
$$Ц= {5}/{9} ({5}/{9})$$
$$Ц= {25} /{81} (што је = 1)$$
Повећање од $5/9$ степени Фаренхајта доводи до повећања од ${25}/{81}$, а не за 1 степен Целзијуса, тако да изјава ИИИ није тачна.
Коначан одговор је Д.
Питање 2
Једначина${24к^2 + 25к -47}/{ак-2} = -8к-3-{53/{ак-2}}$важи за све вредности $к=2/а$, где је $а$ константа.
Која је вредност $а$?
А) -16
Б) -3
Ц) 3
Д) 16
ОБЈАШЊЕЊЕ ОДГОВОРА: Постоје два начина да се ово питање реши. Бржи начин је да помножите сваку страну дате једначине са $ак-2$ (тако да можете да се ослободите разломка). Када помножите сваку страну са $ак-2$, требало би да имате:
$$24к^2 + 25к - 47 = (-8к-3)(ак-2) - 53$$
Затим би требало да помножите $(-8к-3)$ и $(ак-2)$ користећи ФОИЛ.
$$24к^2 + 25к - 47 = -8ак^2 - 3ак +16к + 6 - 53$$
Затим смањите на десној страни једначине
$$24к^2 + 25к - 47 = -8ак^2 - 3ак +16к - 47$$
Пошто коефицијенти $к^2$-члана морају бити једнаки на обе стране једначине, $−8а = 24$, или $а = −3$.
Друга опција која је дужа и досаднија је да покушате да укључите све изборе одговора за а и видите који избор одговора чини обе стране једначине једнакима. Опет, ово је дужа опција и не препоручујем је за стварни САТ јер ће изгубити превише времена.
Коначни одговор је Б.
Питање 3
Ако је $3к-и = 12$, колика је вредност ${8^к}/{2^и}$?
А) $2^{12}$
Б) $4^4$
Ц) $8^2$
Д) Вредност се не може утврдити из датих информација.
ОБЈАШЊЕЊЕ ОДГОВОРА: Један приступ је изражавање
$${8^к}/{2^и}$$
тако да су бројилац и именилац изражени истом основом. Пошто су 2 и 8 оба степена од 2, замена $2^3$ за 8 у бројиоцу од ${8^к}/{2^и}$ даје
$${(2^3)^к}/{2^и}$$
који се може преписати
$${2^3к}/{2^и}$$
Пошто бројилац и именилац имају заједничку основу, овај израз се може преписати као $2^(3к−и)$. У питању се наводи да је $3к − и = 12$, па се експонент, $3к − и$ може заменити са 12, што значи да
$${8^к}/{2^и}= 2^12$$
Коначан одговор је А.
Питање 4
Тачке А и Б леже на кругу полупречника 1, а лук ${АБ}↖⌢$ има дужину од $π/3$. Колики део обима круга је дужина лука ${АБ}↖⌢$?
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте сазнали одговор на ово питање, прво ћете морати да знате формулу за проналажење обима круга.
Обим, $Ц$, круга је $Ц = 2πр$, где је $р$ полупречник круга. За дати круг полупречника 1, обим је $Ц = 2(π)(1)$, или $Ц = 2π$.
Да бисте сазнали колики је део обима дужине ${АБ}↖⌢$, поделите дужину лука са обимом, што даје $π/3 ÷ 2π$. Ова подела се може представити са $π/3 * {1/2}π = 1/6$.
Разломак $1/6$ се такође може преписати као $0,166$ или $0,167$.
Коначни одговор је $1/6$, $0,166$ или $0,167$.
Питање 5
$${8-и}/{3-2и}$$
Ако се горњи израз препише у облику $а+би$, где су $а$ и $б$ реални бројеви, колика је вредност $а$? (Напомена: $и=√{-1}$)
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте преписали ${8-и}/{3-2и}$ у стандардном облику $а + би$, потребно је да помножите бројилац и именилац од ${8-и}/{3-2и}$ коњугатом , $3 + 2и$. Ово је једнако
$$({8-и}/{3-2и})({3+2и}/{3+2и})={24+16и-3+(-и)(2и)}/{(3^2 )-(2и)^2}$$
Пошто $и^2=-1$, овај последњи разломак се може поједноставити на
$$ {24+16и-3и+2}/{9-(-4)}={26+13и}/{13}$$
што даље поједностављује на $2 + и$. Стога, када се ${8-и}/{3-2и}$ поново напише у стандардном облику а + би, вредност а је 2.
Коначан одговор је А.
Питање 6
У троуглу $АБЦ$, мера $∠Б$ је 90°, $БЦ=16$ и $АЦ$=20. Троугао $ДЕФ$ је сличан троуглу $АБЦ$, где врхови $Д$, $Е$ и $Ф$ одговарају теменима $А$, $Б$ и $Ц$, респективно, и свакој страни троугла $ ДЕФ$ је $1/3$ дужина одговарајуће странице троугла $АБЦ$. Која је вредност $синФ$?
ОБЈАШЊЕЊЕ ОДГОВОРА: Троугао АБЦ је правоугли троугао са правим углом у Б. Према томе, $ов {АЦ}$ је хипотенуза правоуглог троугла АБЦ, а $ов {АБ}$ и $ов {БЦ}$ су катете правоугли троугао АБЦ. Према Питагориној теореми,
$$АБ =√{20^2-16^2}=√{400-256}=√{144}=12$$
Пошто је троугао ДЕФ сличан троуглу АБЦ, са врхом Ф који одговара темену Ц, мера $угла ∠ {Ф}$ једнака је мери $угла ∠ {Ц}$. Дакле, $син Ф = син Ц$. Од дужина страница троугла АБЦ,
$$синФ ={супротно сиде}/{хипотенусе}={АБ}/{АЦ}={12}/{20}={3}/{5}$$
Дакле, $синФ ={3}/{5}$.
Коначни одговор је ${3}/{5}$ или 0,6.
Питања из математике за САТ дозвољена за калкулатор
Питање 7

Непотпуна табела изнад сумира број ученика леворуких и десноруких ученика према полу за ученике осмог разреда средње школе Кеисел. Десноруких ученица има 5 пута више него леворуких, а 9 пута више дешњака него леворуких ученика. ако у школи има укупно 18 леворуких ученика и 122 дешњака, шта је од следећег најближе вероватноћи да је случајно одабран дешњак женског пола? (Напомена: Претпоставимо да ниједан ученик осмог разреда није и дешњак и леворук.)
А) 0,410
Б) 0,357
Ц) 0,333
Д) 0,250
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте решили овај проблем, требало би да направите две једначине користећи две променљиве ($к$ и $и$) и информације које сте добили. Нека је $к$ број леворуких ученица и нека је $и$ број леворуких ученика. Користећи информације дате у задатку, број дешњака ће бити $5к$, а број дешњака ће бити $9и$. Пошто је укупан број леворуких ученика 18, а укупан број дешњака 122, систем једначина испод мора да буде тачан:
$$к + и = 18$$
$$5к + 9и = 122$$
Када решите овај систем једначина, добијате $к = 10$ и $и = 8$. Дакле, 5*10, односно 50, од 122 дешњака су жене. Према томе, вероватноћа да је дешњак изабран насумично женско је ${50}/{122}$, што је на најближи хиљадити део 0,410.
Коначан одговор је А.Питања 8 и 9
Користите следеће информације и за питање 7 и за питање 8.
Ако купци уђу у продавницу просечном брзином од $р$ купаца по минуту и сваки остане у продавници просечно време од $Т$ минута, даје се просечан број купаца у продавници, $Н$, у било ком тренутку по формули $Н=рТ$. Овај однос је познат као Литлов закон.
Власник Гоод Деалс Сторе-а процењује да током радног времена у продавницу уђу у просеку 3 купца у минуту и да се сваки од њих задржава у просеку 15 минута. Власник продавнице користи Литлов закон да процени да у продавници у сваком тренутку има 45 купаца.
Питање 8
Литтлеов закон се може применити на било који део продавнице, као што је одређено одељење или редови на благајни. Власник продавнице утврђује да током радног времена отприлике 84 купца по сату обави куповину и сваки од ових купаца проведе у просеку 5 минута на каси. У било ком тренутку током радног времена, колико отприлике купаца у просеку чека у реду за касу да обави куповину у продавници Гоод Деалс?
ОБЈАШЊЕЊЕ ОДГОВОРА: Пошто питање каже да се Литлов закон може применити на било који део продавнице (на пример, само на ред за одјаву), онда је просечан број купаца, $Н$, у реду за одјаву у било ком тренутку $Н = рТ $, где је $р$ број купаца који улазе у ред за одјаву по минуту, а $Т$ је просечан број минута које сваки купац проведе у реду за плаћање.
Пошто 84 купца на сат обави куповину, 84 купца по сату улази у ред за одјаву. Међутим, ово треба да се конвертује у број купаца у минути (да би се користило са $Т = 5$). Пошто у једном сату има 60 минута, цена је {84 $ купаца по сату}/{60 минута} = 1,4$ купаца по минуту. Коришћење дате формуле са $р = 1.4$ и $Т = 5$ даје принос
$$Н = рт = (1.4)(5) = 7$$
Према томе, просечан број купаца, $Н$, у реду за касу у било ком тренутку током радног времена је 7.
Коначан одговор је 7.
Питање 9
Власник продавнице Гоод Деалс отвара нову продавницу широм града. За нову радњу, власник процењује да ће током радног времена у просеку бити око 90 купаца посатуђу у продавницу и сваки од њих остаје у просеку 12 минута. Просечан број купаца у новој продавници у било ком тренутку је који проценат мањи од просечног броја купаца у оригиналној продавници у било ком тренутку? (Напомена: Занемарите симбол за проценат када уносите свој одговор. На пример, ако је одговор 42,1%, унесите 42,1)
ОБЈАШЊЕЊЕ ОДГОВОРА: Према првобитним информацијама, процењени просечан број купаца у првобитној продавници у било ком тренутку (Н) је 45. У питању се наводи да у новој продавници менаџер процењује да је просечно 90 купаца на сат (60 минута) уђите у продавницу, што је еквивалентно 1,5 купаца у минути (р). Менаџер такође процењује да сваки купац остаје у продавници у просеку 12 минута (Т). Дакле, према Литловом закону, у новој продавници у било ком тренутку има, у просеку, $Н = рТ = (1,5)(12) = 18$ купаца. Ово је
$${45-18}/{45} * 100 = 60$$
проценат мање од просечног броја купаца у оригиналној продавници у било ком тренутку.
Коначан одговор је 60.
Питање 10
У $ки$-равни, тачка $(п,р)$ лежи на правој са једначином $и=к+б$, где је $б$ константа. Тачка са координатама $(2п, 5р)$ лежи на правој са једначином $и=2к+б$. Ако је $п=0$, колика је вредност $р/п$?
А) $2/5$
Б) $3/4$
Ц) $4/3$
Д) $5/2$
ОБЈАШЊЕЊЕ ОДГОВОРА: Пошто тачка $(п,р)$ лежи на правој са једначином $и=к+б$, та тачка мора да задовољи једначину. Замена $п$ за $к$ и $р$ за $и$ у једначини $и=к+б$ даје $р=п+б$, или $би б$ = $би р-би п $.
Слично томе, пошто тачка $(2п,5р)$ лежи на правој са једначином $и=2к+б$, тачка мора да задовољава једначину. Замена $2п$ за $к$ и $5р$ за $и$ у једначини $и=2к+б$ даје:
$5р=2(2п)+б$
$5р=4п+б$
$би б$ = $бо 5 би р-бо 4би п$.
Затим, можемо поставити две једначине једнаке $б$ једна другој и поједноставити:
$б=р-п=5р-4п$
$3п=4р$
Коначно, да бисмо пронашли $р/п$, морамо да поделимо обе стране једначине са $п$ и са $4$:
$3п=4р$
$3={4р}/п$
$3/4=р/п$
Тачан одговор је Б , $3/4$.
Ако сте изабрали изборе А и Д, можда сте погрешно формирали свој одговор од коефицијената у тачки $(2п, 5р)$. Ако сте изабрали избор Ц, можда сте побркали $р$ и $п$.
Имајте на уму да док се ово налази у одељку за калкулатор САТ-а, апсолутно вам није потребан ваш калкулатор да бисте га решили!
Питање 11
 Силос за жито је изграђен од два десна кружна конуса и десног кружног цилиндра са унутрашњим мерама приказаним на слици изнад. Од следећег, који је најближи запремини силоса за зрно, у кубним стопама?
Силос за жито је изграђен од два десна кружна конуса и десног кружног цилиндра са унутрашњим мерама приказаним на слици изнад. Од следећег, који је најближи запремини силоса за зрно, у кубним стопама?
А) 261,8
Б) 785,4
Ц) 916.3
Д) 1047.2
ОБЈАШЊЕЊЕ ОДГОВОРА: Запремина силоса за зрно може се наћи додавањем запремина свих чврстих материја од којих се састоји (цилиндра и два конуса). Силос се састоји од цилиндра (висине 10 стопа и полупречника основе 5 стопа) и два конуса (сваки са висином 5 стопа и полупречником основе 5 стопа). Формуле дате на почетку одељка САТ математике:
Запремина конуса
$$В={1}/{3}πр^2х$$
Запремина цилиндра
$$В=πр^2х$$
може се користити за одређивање укупне запремине силоса. Пошто два конуса имају идентичне димензије, укупна запремина силоса, у кубним стопама, дата је као
$$В_{сило}=π(5^2)(10)+(2)({1}/{3})π(5^2)(5)=({4}/{3})(250 )п$$
што је приближно једнако 1.047,2 кубних стопа.
Коначан одговор је Д.
Питање 12
Ако је $к$ просек (аритметичка средина) од $м$ и $9$, $и$ је просек од $2м$ и $15$, а $з$ је просек од $3м$ и $18$, шта је просек од $к$, $и$ и $з$ у смислу $м$?
А) $м+6$
Б) $м+7$
Ц) 2 милиона долара + 14 долара
Д) 3 милиона долара + 21 долара
ОБЈАШЊЕЊЕ ОДГОВОРА: Пошто је просек (аритметичка средина) два броја једнак збиру два броја подељен са 2, једначине $к={м+9}/{2}$, $и={2м+15}/{2 }$, $з={3м+18}/{2}$ су тачне. Просек за $к$, $и$ и $з$ је дат са ${к + и + з}/{3}$. Замена израза у м за сваку променљиву ($к$, $и$, $з$) даје
$$[{м+9}/{2}+{2м+15}/{2}+{3м+18}/{2}]/3$$
Овај разломак се може поједноставити на $м + 7$.
Коначни одговор је Б.
Питање 13
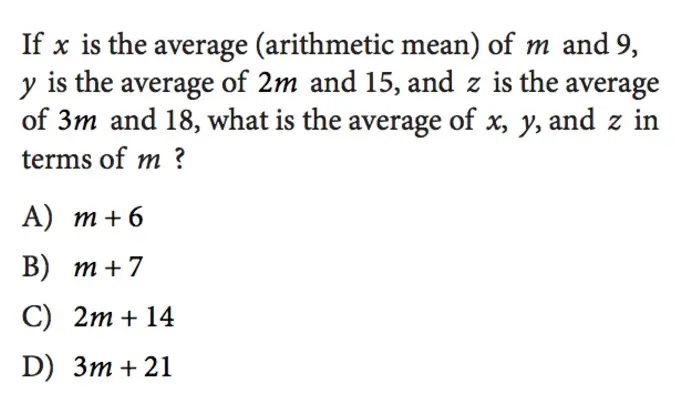
Функција $ф(к)=к^3-к^2-к-{11/4}$ је графички приказана у горњој $ки$-равни. Ако је $к$ константа таква да једначина $ф(к)=к$ има три реална решења, које од следећег може бити вредност $к$?
ОБЈАШЊЕЊЕ ОДГОВОРА: Једначина $ф(к) = к$ даје решења система једначина
$$и = ф(к) = к^3-к^2-к-{11}/{4}$$
и
$$и = к$$
Реално решење система две једначине одговара тачки пресека графика двеју једначина у $ки$-равни.
График $и = к$ је хоризонтална линија која садржи тачку $(0, к)$ и три пута сече график кубичне једначине (пошто има три реална решења). С обзиром на график, једина хоризонтална линија која би три пута пресекла кубну једначину је линија са једначином $и = −3$, или $ф(к) = −3$. Дакле, $к$ је $-3$.
Коначан одговор је Д.
Питање 14
$$к={1/2}нв^2$$
Динамички притисак $к$ генерисан флуидом који се креће брзином $в$ може се наћи коришћењем формуле изнад, где је $н$ константна густина течности. Аеронаутички инжењер користи формулу да пронађе динамички притисак флуида који се креће брзином $в$ и исте течности која се креће брзином 1,5$в$. Колики је однос динамичког притиска бржег флуида и динамичког притиска спорије течности?
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте решили овај проблем, потребно је да поставите једначине са променљивим. Нека је $к_1$ динамички притисак спорије течности која се креће брзином $в_1$, а нека је $к_2$ динамички притисак брже течности која се креће брзином $в_2$. Онда
$$в_2 =1,5в_1$$
Узимајући у обзир једначину $к = {1}/{2}нв^2$, замена динамичког притиска и брзине бржег флуида даје $к_2 = {1}/{2}н(в_2)^2$. Пошто је $в_2 =1.5в_1$, израз $1.5в_1$ може бити замењен са $в_2$ у овој једначини, дајући $к_2 = {1}/{2}н(1.5в_1)^2$. Узимајући на квадрат $1,5$, можете преписати претходну једначину као
$$к_2 = (2.25)({1}/{2})н(в_1)^2 = (2.25)к_1$$
Дакле, однос динамичког притиска бржег флуида је
$${к2}/{к1} = {2,25 к_1}/{к_1}= 2,25 $$
Коначан одговор је 2,25 или 9/4.
Питање 15
За полином $п(к)$, вредност $п(3)$ је $-2$. Шта од следећег мора бити тачно за $п(к)$?
А) $к-5$ је фактор од $п(к)$.
Б) $к-2$ је фактор од $п(к)$.
Ц) $к+2$ је фактор од $п(к)$.
Д) Остатак када се $п(к)$ подели са $к-3$ је $-2$.
ОБЈАШЊЕЊЕ ОДГОВОРА: Ако је полином $п(к)$ подељен полиномом облика $к+к$ (који обухвата све могуће изборе одговора у овом питању), резултат се може написати као
$${п(к)}/{к+к}=к(к)+{р}/{к+к}$$
где је $к(к)$ полином, а $р$ остатак. Пошто је $к + к$ полином степена 1 (што значи да укључује само $к^1$ и нема виших експонента), остатак је реалан број.
Према томе, $п(к)$ се може преписати као $п(к) = (к + к)к(к) + р$, где је $р$ реалан број.
Питање гласи да је $п(3) = -2$, тако да мора бити тачно да
$$-2 = п(3) = (3 + к)к(3) + р$$
Сада можемо укључити све могуће одговоре. Ако је одговор А, Б или Ц, $р$ ће бити $0$, док ако је одговор Д, $р$ ће бити $-2$.
А. $-2 = п(3) = (3 + (-5))к(3) + 0$
$-2=(3-5)к(3)$
$-2=(-2)к(3)$
Ово би могло бити тачно, али само ако је $к(3)=1$
Б. $-2 = п(3) = (3 + (-2))к(3) + 0$
$-2 = (3-2)к(3)$
$-2 = (-1)к(3)$
Ово би могло бити тачно, али само ако је $к(3)=2$
Ц. $-2 = п(3) = (3 + 2)к(3) + 0$
$-2 = (5)к(3)$
Ово би могло бити тачно, али само ако је $к(3)={-2}/{5}$
Д. $-2 = п(3) = (3 + (-3))к(3) + (-2)$
$-2 = (3 - 3)к(3) + (-2)$
$-2 = (0)к(3) + (-2)$
Ово ће увек буди истинит без обзира шта је $к(3)$.
Од избора одговора, једини који мора ако је тачно да је $п(к)$ Д, да је остатак када се $п(к)$ подели са $к-3$ -2.
Коначан одговор је Д.

Заслужујеш све дремке након што прођеш кроз та питања.
Шта је заједничко најтежим САТ математичким питањима?
Важно је разумети шта ова тешка питања чини „тешким“. На тај начин ћете моћи да разумете и решите слична питања када их видите на дан тестирања, као и да имате бољу стратегију за идентификацију и исправљање ваших претходних САТ математичких грешака.
У овом одељку ћемо погледати шта ова питања имају заједничко и дати примере сваке врсте. Неки од разлога зашто су најтежа математичка питања најтежа математичка питања су:
#1: Тестирајте неколико математичких концепата одједном

Овде морамо да се бавимо замишљеним бројевима и разломцима одједном.
Тајна успеха: Размислите коју применљиву математику можете користити да решите проблем, радите корак по корак и испробајте сваку технику док не пронађете ону која функционише!
#2: Укључује много корака
Запамтите: што више корака треба да предузмете, лакше ћете забрљати негде на линији!
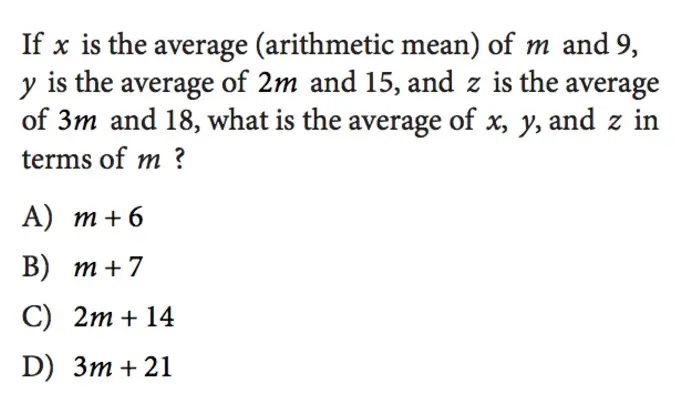
Морамо да решимо овај проблем у корацима (радећи неколико просека) да бисмо откључали остатак одговора у домино ефекту. Ово може бити збуњујуће, посебно ако сте под стресом или вам понестаје времена.
Тајна успеха: Полако, идите корак по корак и још једном проверите свој рад како не бисте погрешили!
#3: Тестирајте концепте са којима сте ограничено упознати
На пример, многи ученици су мање упознати са функцијама него са разломцима и процентима, тако да се већина функционалних питања сматра проблемима „високе тежине“.

Ако не знате како се сналазите у функцијама, ово би био тежак проблем.
Тајна успеха: Прегледајте математичке концепте са којима нисте толико упознати, као што су функције. Предлажемо да користите наше сјајне бесплатне САТ Матх водиче за преглед.
#4: Написане су на необичне или замршене начине
Може бити тешко схватити која су тачно нека питања питајући , а још мање схватити како их решити. Ово је посебно тачно када се питање налази на крају одељка, а понестаје вам времена.

Пошто ово питање пружа толико информација без дијаграма, може бити тешко загонетнути у ограниченом дозвољеном времену.
Тајна успеха: Узмите си времена, анализирајте шта се од вас тражи и нацртајте дијаграм ако вам је од помоћи.
#5: Користите много различитих варијабли

Са толико различитих варијабли у игри, прилично је лако доћи до забуне.
Тајна успеха: Узмите си времена, анализирајте шта се од вас тражи и размислите да ли је додавање бројева добра стратегија за решавање проблема (то не би било за горње питање, али би било за многа друга питања о променљивој САТ).
Тхе Таке-Аваис
САТ је маратон и што сте боље припремљени за њега, боље ћете се осећати на дан тестирања. Ако знате како да се носите са најтежим питањима која вам тест може поставити, чиниће полагање правог САТ-а много мање застрашујућим.
Ако сте сматрали да су ова питања лака, пазите да не потцењујете ефекат адреналина и умора на вашу способност решавања проблема. Док настављате да учите, увек се придржавајте одговарајућих смерница за време и покушајте да урадите пуне тестове кад год је то могуће. Ово је најбољи начин да поново креирате стварно окружење за тестирање како бисте се могли припремити за прави посао.
Ако сматрате да су ова питања изазовна, обавезно ојачајте своје знање математике тако што ћете погледати наше индивидуалне математичке водиче за САТ. Тамо ћете видети детаљнија објашњења тема о којима је реч, као и детаљније рашчлањивање одговора.
Шта је следеће?
Осетили сте да су ова питања тежа него што сте очекивали? Погледајте све теме обухваћене у САТ одељку из математике, а затим забележите који одељци су вам представљали посебну потешкоћу. Затим погледајте наше индивидуалне математичке водиче који ће вам помоћи да учврстите било коју од тих слабих области.
Понестаје вам времена за САТ математичку секцију? Наш водич ће вам помоћи да победите сат и повећате свој резултат.
Циљате на савршен резултат? Провери наш водич о томе како да добијете савршених 800 на САТ одељку из математике , који је написао савршени стрелац.
,167$.
Коначни одговор је /6$, 
Желите да се тестирате против најтежих САТ математичких питања? Желите да знате шта ова питања чини тако тешким и како их најбоље решити? Ако сте спремни да заиста утонете своје зубе у САТ одељак из математике и усредсредите се на савршен резултат, онда је ово водич за вас.
Саставили смо оно што верујемо да јесте 15 најтежих питања за тренутни САТ , са стратегијама и објашњењима одговора за сваки. Ово су све тешка САТ математичка питања са САТ тестова за вежбање Цоллеге Боард-а, што значи да је њихово разумевање један од најбољих начина за учење за оне од вас који теже савршенству.
Слика: Сониа Севилла /Викимедија
Кратак преглед САТ Матх
Трећи и четврти део САТ увек ће бити математички део . Први математички пододељак (означен са '3') ради не омогућавају вам да користите калкулатор, док је други математички пододељак (означен са '4') ради дозволити коришћење калкулатора. Међутим, не брините превише о одељку без калкулатора: ако вам није дозвољено да користите калкулатор за питање, то значи да вам није потребан калкулатор да бисте одговорили на њега.
Сваки математички пододељак је распоређен по растућој тежини (где је дуже потребно да се реши проблем и што мање људи на њега тачно одговори, то је теже). У сваком пододељку, питање 1 ће бити „лако“, а питање 15 ће се сматрати „тешким“. Међутим, растућа потешкоћа се ресетује са лаке на тешку на мрежи.
Дакле, питања са вишеструким избором су распоређена по растућој тежини (питања 1 и 2 ће бити најлакша, питања 14 и 15 ће бити најтежа), али ниво тежине се ресетује за одељак мреже (што значи да ће питања 16 и 17 поново бити 'лако', а питања 19 и 20 ће бити веома тешка).
Уз врло мало изузетака, дакле, најтежи САТ математички задаци ће бити групирани на крају сегмената са вишеструким избором или у другој половини питања у мрежи. Међутим, поред њиховог постављања на тест, ова питања имају и неколико других заједничких карактеристика. За минут ћемо погледати примере питања и како да их решимо, а затим их анализирамо да бисмо открили шта је заједничко овим врстама питања.
Али прво: да ли би требало да се сада фокусирате на најтежа математичка питања?
Ако тек почињете са припремама за учење (или ако сте једноставно прескочили овај први, кључни корак), дефинитивно престаните и урадите потпуни тест да бисте проценили свој тренутни ниво бодова. Погледајте наш водич за сви бесплатни САТ тестови за вежбање доступни на мрежи а затим седите да урадите тест одједном.
Апсолутно најбољи начин да процените свој тренутни ниво је да једноставно урадите САТ тест као да је стваран, држећи стриктно време и радећи директно са само дозвољеним паузама (знамо - вероватно није ваш омиљени начин да проведете суботу). Када стекнете добру представу о свом тренутном нивоу и процентуалном рангирању, можете поставити прекретнице и циљеве за свој коначни резултат САТ математике.
Ако тренутно постижете резултате у распону од 200-400 или 400-600 на САТ математици, најбоље је да прво погледате наш водич за побољшање вашег математичког резултата да стално будете на или преко 600 пре него што почнете да покушавате да се ухватите у коштац са најтежим математичким проблемима на тесту.
Међутим, ако већ постижете више од 600 поена у одељку из математике и желите да тестирате своју снагу за прави САТ, онда свакако пређите на остатак овог водича. Ако тежите савршеном (или близу) , онда ћете морати да знате како изгледају најтежа САТ математичка питања и како да их решите. И на срећу, управо то ћемо и урадити.
УПОЗОРЕЊЕ: Пошто постоји ограничен број званични САТ практични тестови , можда ћете желети да сачекате да прочитате овај чланак док не покушате све или већину прва четири званична теста за вежбање (пошто је већина питања у наставку преузета из тих тестова). Ако сте забринути да не покварите те тестове, престаните сада да читате овај водич; вратите се и прочитајте када их завршите.

Хајде сада да пређемо на нашу листу питања (вхоо)!
Слика: Ниитк /ДевиантАрт
15 најтежих САТ математичких питања
Сада када сте сигурни да би требало да покушате са оваквим питањима, хајде да одмах уђемо! У наставку смо припремили 15 најтежих САТ математичких питања које можете испробати, заједно са упутствима о томе како да добијете одговор (ако сте збуњени).
Нема калкулатора САТ математичких питања
Питање 1
$$Ц=5/9(Ф-32)$$
Горња једначина показује како је температура $Ф$, мерена у степенима Фаренхајта, повезана са температуром $Ц$, мереном у степенима Целзијуса. На основу једначине, шта од следећег мора бити тачно?
- Повећање температуре од 1 степен Фаренхајта је еквивалентно повећању температуре од 5/9$ степени Целзијуса.
- Повећање температуре од 1 степен Целзијуса је еквивалентно повећању температуре од 1,8 степени Фаренхајта.
- Повећање температуре од $5/9$ степени Фаренхајта је еквивалентно порасту температуре од 1 степен Целзијуса.
А) Само ја
Б) Само ИИ
Ц) Само ИИИ
Д) само И и ИИ
ОБЈАШЊЕЊЕ ОДГОВОРА: Замислите једначину као једначину за праву
$$и=мк+б$$
где у овом случају
$$Ц= {5}/{9} (Ф−32)$$
или
$$Ц={5}/{9}Ф −{5}/{9}(32)$$
Можете да видите да је нагиб графика ${5}/{9}$, што значи да је за повећање од 1 степен Фаренхајта повећање износи ${5}/{9}$ од 1 степен Целзијуса.
$$Ц= {5}/{9} (Ф)$$
$$Ц= {5}/{9} (1)= {5}/{9}$$
Дакле, изјава И је тачна. Ово је еквивалентно томе да кажемо да је повећање од 1 степен Целзијуса једнако повећању од ${9}/{5}$ степени Фаренхајта.
$$Ц= {5}/{9} (Ф)$$
$$1= {5}/{9} (Ф)$$
$$(Ф)={9}/{5}$$
Пошто је ${9}/{5}$ = 1,8, изјава ИИ је тачна.
Једини одговор који има и исказ И и исказ ИИ као тачан је Д , али ако имате времена и желите да будете потпуно темељни, такође можете да проверите да ли је изјава ИИИ (повећање од ${5}/{9}$ степен Фаренхајта једнако повећању температуре од 1 степен Целзијуса) тачна :
$$Ц= {5}/{9} (Ф)$$
$$Ц= {5}/{9} ({5}/{9})$$
$$Ц= {25} /{81} (што је = 1)$$
Повећање од $5/9$ степени Фаренхајта доводи до повећања од ${25}/{81}$, а не за 1 степен Целзијуса, тако да изјава ИИИ није тачна.
Коначан одговор је Д.
Питање 2
Једначина${24к^2 + 25к -47}/{ак-2} = -8к-3-{53/{ак-2}}$важи за све вредности $к=2/а$, где је $а$ константа.
Која је вредност $а$?
А) -16
Б) -3
Ц) 3
Д) 16
ОБЈАШЊЕЊЕ ОДГОВОРА: Постоје два начина да се ово питање реши. Бржи начин је да помножите сваку страну дате једначине са $ак-2$ (тако да можете да се ослободите разломка). Када помножите сваку страну са $ак-2$, требало би да имате:
$$24к^2 + 25к - 47 = (-8к-3)(ак-2) - 53$$
Затим би требало да помножите $(-8к-3)$ и $(ак-2)$ користећи ФОИЛ.
$$24к^2 + 25к - 47 = -8ак^2 - 3ак +16к + 6 - 53$$
Затим смањите на десној страни једначине
$$24к^2 + 25к - 47 = -8ак^2 - 3ак +16к - 47$$
Пошто коефицијенти $к^2$-члана морају бити једнаки на обе стране једначине, $−8а = 24$, или $а = −3$.
Друга опција која је дужа и досаднија је да покушате да укључите све изборе одговора за а и видите који избор одговора чини обе стране једначине једнакима. Опет, ово је дужа опција и не препоручујем је за стварни САТ јер ће изгубити превише времена.
Коначни одговор је Б.
Питање 3
Ако је $3к-и = 12$, колика је вредност ${8^к}/{2^и}$?
А) $2^{12}$
Б) $4^4$
Ц) $8^2$
Д) Вредност се не може утврдити из датих информација.
ОБЈАШЊЕЊЕ ОДГОВОРА: Један приступ је изражавање
$${8^к}/{2^и}$$
тако да су бројилац и именилац изражени истом основом. Пошто су 2 и 8 оба степена од 2, замена $2^3$ за 8 у бројиоцу од ${8^к}/{2^и}$ даје
$${(2^3)^к}/{2^и}$$
који се може преписати
$${2^3к}/{2^и}$$
Пошто бројилац и именилац имају заједничку основу, овај израз се може преписати као $2^(3к−и)$. У питању се наводи да је $3к − и = 12$, па се експонент, $3к − и$ може заменити са 12, што значи да
$${8^к}/{2^и}= 2^12$$
Коначан одговор је А.
Питање 4
Тачке А и Б леже на кругу полупречника 1, а лук ${АБ}↖⌢$ има дужину од $π/3$. Колики део обима круга је дужина лука ${АБ}↖⌢$?
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте сазнали одговор на ово питање, прво ћете морати да знате формулу за проналажење обима круга.
Обим, $Ц$, круга је $Ц = 2πр$, где је $р$ полупречник круга. За дати круг полупречника 1, обим је $Ц = 2(π)(1)$, или $Ц = 2π$.
Да бисте сазнали колики је део обима дужине ${АБ}↖⌢$, поделите дужину лука са обимом, што даје $π/3 ÷ 2π$. Ова подела се може представити са $π/3 * {1/2}π = 1/6$.
Разломак $1/6$ се такође може преписати као $0,166$ или $0,167$.
Коначни одговор је $1/6$, $0,166$ или $0,167$.
Питање 5
$${8-и}/{3-2и}$$
Ако се горњи израз препише у облику $а+би$, где су $а$ и $б$ реални бројеви, колика је вредност $а$? (Напомена: $и=√{-1}$)
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте преписали ${8-и}/{3-2и}$ у стандардном облику $а + би$, потребно је да помножите бројилац и именилац од ${8-и}/{3-2и}$ коњугатом , $3 + 2и$. Ово је једнако
$$({8-и}/{3-2и})({3+2и}/{3+2и})={24+16и-3+(-и)(2и)}/{(3^2 )-(2и)^2}$$
Пошто $и^2=-1$, овај последњи разломак се може поједноставити на
$$ {24+16и-3и+2}/{9-(-4)}={26+13и}/{13}$$
што даље поједностављује на $2 + и$. Стога, када се ${8-и}/{3-2и}$ поново напише у стандардном облику а + би, вредност а је 2.
Коначан одговор је А.
Питање 6
У троуглу $АБЦ$, мера $∠Б$ је 90°, $БЦ=16$ и $АЦ$=20. Троугао $ДЕФ$ је сличан троуглу $АБЦ$, где врхови $Д$, $Е$ и $Ф$ одговарају теменима $А$, $Б$ и $Ц$, респективно, и свакој страни троугла $ ДЕФ$ је $1/3$ дужина одговарајуће странице троугла $АБЦ$. Која је вредност $синФ$?
ОБЈАШЊЕЊЕ ОДГОВОРА: Троугао АБЦ је правоугли троугао са правим углом у Б. Према томе, $ов {АЦ}$ је хипотенуза правоуглог троугла АБЦ, а $ов {АБ}$ и $ов {БЦ}$ су катете правоугли троугао АБЦ. Према Питагориној теореми,
$$АБ =√{20^2-16^2}=√{400-256}=√{144}=12$$
Пошто је троугао ДЕФ сличан троуглу АБЦ, са врхом Ф који одговара темену Ц, мера $угла ∠ {Ф}$ једнака је мери $угла ∠ {Ц}$. Дакле, $син Ф = син Ц$. Од дужина страница троугла АБЦ,
$$синФ ={супротно сиде}/{хипотенусе}={АБ}/{АЦ}={12}/{20}={3}/{5}$$
Дакле, $синФ ={3}/{5}$.
Коначни одговор је ${3}/{5}$ или 0,6.
Питања из математике за САТ дозвољена за калкулатор
Питање 7

Непотпуна табела изнад сумира број ученика леворуких и десноруких ученика према полу за ученике осмог разреда средње школе Кеисел. Десноруких ученица има 5 пута више него леворуких, а 9 пута више дешњака него леворуких ученика. ако у школи има укупно 18 леворуких ученика и 122 дешњака, шта је од следећег најближе вероватноћи да је случајно одабран дешњак женског пола? (Напомена: Претпоставимо да ниједан ученик осмог разреда није и дешњак и леворук.)
А) 0,410
Б) 0,357
Ц) 0,333
Д) 0,250
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте решили овај проблем, требало би да направите две једначине користећи две променљиве ($к$ и $и$) и информације које сте добили. Нека је $к$ број леворуких ученица и нека је $и$ број леворуких ученика. Користећи информације дате у задатку, број дешњака ће бити $5к$, а број дешњака ће бити $9и$. Пошто је укупан број леворуких ученика 18, а укупан број дешњака 122, систем једначина испод мора да буде тачан:
$$к + и = 18$$
$$5к + 9и = 122$$
Када решите овај систем једначина, добијате $к = 10$ и $и = 8$. Дакле, 5*10, односно 50, од 122 дешњака су жене. Према томе, вероватноћа да је дешњак изабран насумично женско је ${50}/{122}$, што је на најближи хиљадити део 0,410.
Коначан одговор је А.Питања 8 и 9
Користите следеће информације и за питање 7 и за питање 8.
Ако купци уђу у продавницу просечном брзином од $р$ купаца по минуту и сваки остане у продавници просечно време од $Т$ минута, даје се просечан број купаца у продавници, $Н$, у било ком тренутку по формули $Н=рТ$. Овај однос је познат као Литлов закон.
Власник Гоод Деалс Сторе-а процењује да током радног времена у продавницу уђу у просеку 3 купца у минуту и да се сваки од њих задржава у просеку 15 минута. Власник продавнице користи Литлов закон да процени да у продавници у сваком тренутку има 45 купаца.
Питање 8
Литтлеов закон се може применити на било који део продавнице, као што је одређено одељење или редови на благајни. Власник продавнице утврђује да током радног времена отприлике 84 купца по сату обави куповину и сваки од ових купаца проведе у просеку 5 минута на каси. У било ком тренутку током радног времена, колико отприлике купаца у просеку чека у реду за касу да обави куповину у продавници Гоод Деалс?
ОБЈАШЊЕЊЕ ОДГОВОРА: Пошто питање каже да се Литлов закон може применити на било који део продавнице (на пример, само на ред за одјаву), онда је просечан број купаца, $Н$, у реду за одјаву у било ком тренутку $Н = рТ $, где је $р$ број купаца који улазе у ред за одјаву по минуту, а $Т$ је просечан број минута које сваки купац проведе у реду за плаћање.
Пошто 84 купца на сат обави куповину, 84 купца по сату улази у ред за одјаву. Међутим, ово треба да се конвертује у број купаца у минути (да би се користило са $Т = 5$). Пошто у једном сату има 60 минута, цена је {84 $ купаца по сату}/{60 минута} = 1,4$ купаца по минуту. Коришћење дате формуле са $р = 1.4$ и $Т = 5$ даје принос
$$Н = рт = (1.4)(5) = 7$$
Према томе, просечан број купаца, $Н$, у реду за касу у било ком тренутку током радног времена је 7.
Коначан одговор је 7.
Питање 9
Власник продавнице Гоод Деалс отвара нову продавницу широм града. За нову радњу, власник процењује да ће током радног времена у просеку бити око 90 купаца посатуђу у продавницу и сваки од њих остаје у просеку 12 минута. Просечан број купаца у новој продавници у било ком тренутку је који проценат мањи од просечног броја купаца у оригиналној продавници у било ком тренутку? (Напомена: Занемарите симбол за проценат када уносите свој одговор. На пример, ако је одговор 42,1%, унесите 42,1)
ОБЈАШЊЕЊЕ ОДГОВОРА: Према првобитним информацијама, процењени просечан број купаца у првобитној продавници у било ком тренутку (Н) је 45. У питању се наводи да у новој продавници менаџер процењује да је просечно 90 купаца на сат (60 минута) уђите у продавницу, што је еквивалентно 1,5 купаца у минути (р). Менаџер такође процењује да сваки купац остаје у продавници у просеку 12 минута (Т). Дакле, према Литловом закону, у новој продавници у било ком тренутку има, у просеку, $Н = рТ = (1,5)(12) = 18$ купаца. Ово је
$${45-18}/{45} * 100 = 60$$
проценат мање од просечног броја купаца у оригиналној продавници у било ком тренутку.
Коначан одговор је 60.
Питање 10
У $ки$-равни, тачка $(п,р)$ лежи на правој са једначином $и=к+б$, где је $б$ константа. Тачка са координатама $(2п, 5р)$ лежи на правој са једначином $и=2к+б$. Ако је $п=0$, колика је вредност $р/п$?
А) $2/5$
Б) $3/4$
Ц) $4/3$
Д) $5/2$
ОБЈАШЊЕЊЕ ОДГОВОРА: Пошто тачка $(п,р)$ лежи на правој са једначином $и=к+б$, та тачка мора да задовољи једначину. Замена $п$ за $к$ и $р$ за $и$ у једначини $и=к+б$ даје $р=п+б$, или $би б$ = $би р-би п $.
Слично томе, пошто тачка $(2п,5р)$ лежи на правој са једначином $и=2к+б$, тачка мора да задовољава једначину. Замена $2п$ за $к$ и $5р$ за $и$ у једначини $и=2к+б$ даје:
$5р=2(2п)+б$
$5р=4п+б$
$би б$ = $бо 5 би р-бо 4би п$.
Затим, можемо поставити две једначине једнаке $б$ једна другој и поједноставити:
$б=р-п=5р-4п$
$3п=4р$
Коначно, да бисмо пронашли $р/п$, морамо да поделимо обе стране једначине са $п$ и са $4$:
$3п=4р$
$3={4р}/п$
$3/4=р/п$
Тачан одговор је Б , $3/4$.
Ако сте изабрали изборе А и Д, можда сте погрешно формирали свој одговор од коефицијената у тачки $(2п, 5р)$. Ако сте изабрали избор Ц, можда сте побркали $р$ и $п$.
Имајте на уму да док се ово налази у одељку за калкулатор САТ-а, апсолутно вам није потребан ваш калкулатор да бисте га решили!
Питање 11
 Силос за жито је изграђен од два десна кружна конуса и десног кружног цилиндра са унутрашњим мерама приказаним на слици изнад. Од следећег, који је најближи запремини силоса за зрно, у кубним стопама?
Силос за жито је изграђен од два десна кружна конуса и десног кружног цилиндра са унутрашњим мерама приказаним на слици изнад. Од следећег, који је најближи запремини силоса за зрно, у кубним стопама?
А) 261,8
Б) 785,4
Ц) 916.3
Д) 1047.2
ОБЈАШЊЕЊЕ ОДГОВОРА: Запремина силоса за зрно може се наћи додавањем запремина свих чврстих материја од којих се састоји (цилиндра и два конуса). Силос се састоји од цилиндра (висине 10 стопа и полупречника основе 5 стопа) и два конуса (сваки са висином 5 стопа и полупречником основе 5 стопа). Формуле дате на почетку одељка САТ математике:
Запремина конуса
$$В={1}/{3}πр^2х$$
Запремина цилиндра
$$В=πр^2х$$
може се користити за одређивање укупне запремине силоса. Пошто два конуса имају идентичне димензије, укупна запремина силоса, у кубним стопама, дата је као
$$В_{сило}=π(5^2)(10)+(2)({1}/{3})π(5^2)(5)=({4}/{3})(250 )п$$
што је приближно једнако 1.047,2 кубних стопа.
Коначан одговор је Д.
Питање 12
Ако је $к$ просек (аритметичка средина) од $м$ и $9$, $и$ је просек од $2м$ и $15$, а $з$ је просек од $3м$ и $18$, шта је просек од $к$, $и$ и $з$ у смислу $м$?
А) $м+6$
Б) $м+7$
Ц) 2 милиона долара + 14 долара
Д) 3 милиона долара + 21 долара
ОБЈАШЊЕЊЕ ОДГОВОРА: Пошто је просек (аритметичка средина) два броја једнак збиру два броја подељен са 2, једначине $к={м+9}/{2}$, $и={2м+15}/{2 }$, $з={3м+18}/{2}$ су тачне. Просек за $к$, $и$ и $з$ је дат са ${к + и + з}/{3}$. Замена израза у м за сваку променљиву ($к$, $и$, $з$) даје
$$[{м+9}/{2}+{2м+15}/{2}+{3м+18}/{2}]/3$$
Овај разломак се може поједноставити на $м + 7$.
Коначни одговор је Б.
Питање 13
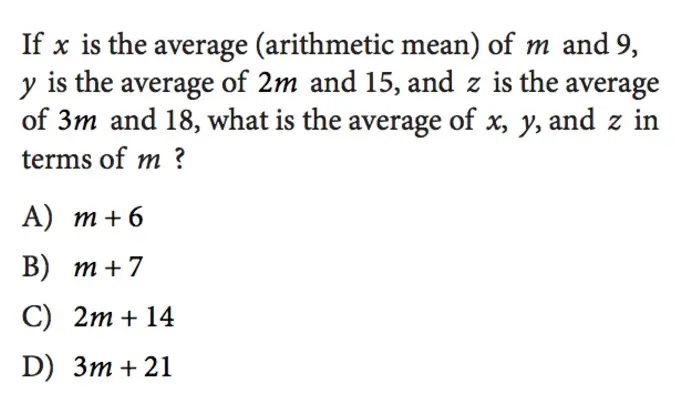
Функција $ф(к)=к^3-к^2-к-{11/4}$ је графички приказана у горњој $ки$-равни. Ако је $к$ константа таква да једначина $ф(к)=к$ има три реална решења, које од следећег може бити вредност $к$?
ОБЈАШЊЕЊЕ ОДГОВОРА: Једначина $ф(к) = к$ даје решења система једначина
$$и = ф(к) = к^3-к^2-к-{11}/{4}$$
и
$$и = к$$
Реално решење система две једначине одговара тачки пресека графика двеју једначина у $ки$-равни.
График $и = к$ је хоризонтална линија која садржи тачку $(0, к)$ и три пута сече график кубичне једначине (пошто има три реална решења). С обзиром на график, једина хоризонтална линија која би три пута пресекла кубну једначину је линија са једначином $и = −3$, или $ф(к) = −3$. Дакле, $к$ је $-3$.
Коначан одговор је Д.
Питање 14
$$к={1/2}нв^2$$
Динамички притисак $к$ генерисан флуидом који се креће брзином $в$ може се наћи коришћењем формуле изнад, где је $н$ константна густина течности. Аеронаутички инжењер користи формулу да пронађе динамички притисак флуида који се креће брзином $в$ и исте течности која се креће брзином 1,5$в$. Колики је однос динамичког притиска бржег флуида и динамичког притиска спорије течности?
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте решили овај проблем, потребно је да поставите једначине са променљивим. Нека је $к_1$ динамички притисак спорије течности која се креће брзином $в_1$, а нека је $к_2$ динамички притисак брже течности која се креће брзином $в_2$. Онда
$$в_2 =1,5в_1$$
Узимајући у обзир једначину $к = {1}/{2}нв^2$, замена динамичког притиска и брзине бржег флуида даје $к_2 = {1}/{2}н(в_2)^2$. Пошто је $в_2 =1.5в_1$, израз $1.5в_1$ може бити замењен са $в_2$ у овој једначини, дајући $к_2 = {1}/{2}н(1.5в_1)^2$. Узимајући на квадрат $1,5$, можете преписати претходну једначину као
$$к_2 = (2.25)({1}/{2})н(в_1)^2 = (2.25)к_1$$
Дакле, однос динамичког притиска бржег флуида је
$${к2}/{к1} = {2,25 к_1}/{к_1}= 2,25 $$
Коначан одговор је 2,25 или 9/4.
Питање 15
За полином $п(к)$, вредност $п(3)$ је $-2$. Шта од следећег мора бити тачно за $п(к)$?
А) $к-5$ је фактор од $п(к)$.
Б) $к-2$ је фактор од $п(к)$.
Ц) $к+2$ је фактор од $п(к)$.
Д) Остатак када се $п(к)$ подели са $к-3$ је $-2$.
ОБЈАШЊЕЊЕ ОДГОВОРА: Ако је полином $п(к)$ подељен полиномом облика $к+к$ (који обухвата све могуће изборе одговора у овом питању), резултат се може написати као
$${п(к)}/{к+к}=к(к)+{р}/{к+к}$$
где је $к(к)$ полином, а $р$ остатак. Пошто је $к + к$ полином степена 1 (што значи да укључује само $к^1$ и нема виших експонента), остатак је реалан број.
Према томе, $п(к)$ се може преписати као $п(к) = (к + к)к(к) + р$, где је $р$ реалан број.
Питање гласи да је $п(3) = -2$, тако да мора бити тачно да
$$-2 = п(3) = (3 + к)к(3) + р$$
Сада можемо укључити све могуће одговоре. Ако је одговор А, Б или Ц, $р$ ће бити $0$, док ако је одговор Д, $р$ ће бити $-2$.
А. $-2 = п(3) = (3 + (-5))к(3) + 0$
$-2=(3-5)к(3)$
$-2=(-2)к(3)$
Ово би могло бити тачно, али само ако је $к(3)=1$
Б. $-2 = п(3) = (3 + (-2))к(3) + 0$
$-2 = (3-2)к(3)$
$-2 = (-1)к(3)$
Ово би могло бити тачно, али само ако је $к(3)=2$
Ц. $-2 = п(3) = (3 + 2)к(3) + 0$
$-2 = (5)к(3)$
Ово би могло бити тачно, али само ако је $к(3)={-2}/{5}$
Д. $-2 = п(3) = (3 + (-3))к(3) + (-2)$
$-2 = (3 - 3)к(3) + (-2)$
$-2 = (0)к(3) + (-2)$
Ово ће увек буди истинит без обзира шта је $к(3)$.
Од избора одговора, једини који мора ако је тачно да је $п(к)$ Д, да је остатак када се $п(к)$ подели са $к-3$ -2.
Коначан одговор је Д.

Заслужујеш све дремке након што прођеш кроз та питања.
Шта је заједничко најтежим САТ математичким питањима?
Важно је разумети шта ова тешка питања чини „тешким“. На тај начин ћете моћи да разумете и решите слична питања када их видите на дан тестирања, као и да имате бољу стратегију за идентификацију и исправљање ваших претходних САТ математичких грешака.
У овом одељку ћемо погледати шта ова питања имају заједничко и дати примере сваке врсте. Неки од разлога зашто су најтежа математичка питања најтежа математичка питања су:
#1: Тестирајте неколико математичких концепата одједном

Овде морамо да се бавимо замишљеним бројевима и разломцима одједном.
Тајна успеха: Размислите коју применљиву математику можете користити да решите проблем, радите корак по корак и испробајте сваку технику док не пронађете ону која функционише!
#2: Укључује много корака
Запамтите: што више корака треба да предузмете, лакше ћете забрљати негде на линији!
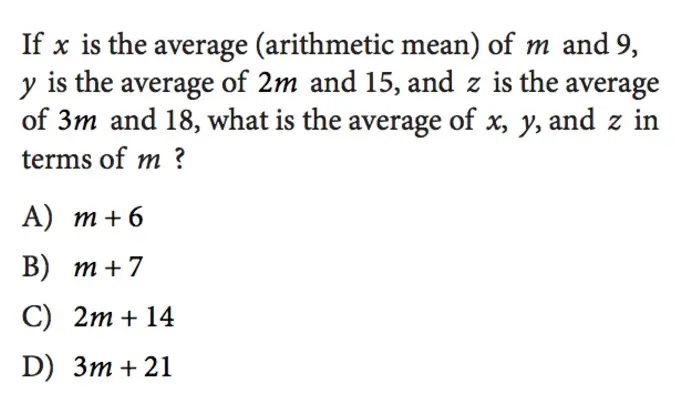
Морамо да решимо овај проблем у корацима (радећи неколико просека) да бисмо откључали остатак одговора у домино ефекту. Ово може бити збуњујуће, посебно ако сте под стресом или вам понестаје времена.
Тајна успеха: Полако, идите корак по корак и још једном проверите свој рад како не бисте погрешили!
#3: Тестирајте концепте са којима сте ограничено упознати
На пример, многи ученици су мање упознати са функцијама него са разломцима и процентима, тако да се већина функционалних питања сматра проблемима „високе тежине“.

Ако не знате како се сналазите у функцијама, ово би био тежак проблем.
Тајна успеха: Прегледајте математичке концепте са којима нисте толико упознати, као што су функције. Предлажемо да користите наше сјајне бесплатне САТ Матх водиче за преглед.
#4: Написане су на необичне или замршене начине
Може бити тешко схватити која су тачно нека питања питајући , а још мање схватити како их решити. Ово је посебно тачно када се питање налази на крају одељка, а понестаје вам времена.

Пошто ово питање пружа толико информација без дијаграма, може бити тешко загонетнути у ограниченом дозвољеном времену.
Тајна успеха: Узмите си времена, анализирајте шта се од вас тражи и нацртајте дијаграм ако вам је од помоћи.
#5: Користите много различитих варијабли

Са толико различитих варијабли у игри, прилично је лако доћи до забуне.
Тајна успеха: Узмите си времена, анализирајте шта се од вас тражи и размислите да ли је додавање бројева добра стратегија за решавање проблема (то не би било за горње питање, али би било за многа друга питања о променљивој САТ).
Тхе Таке-Аваис
САТ је маратон и што сте боље припремљени за њега, боље ћете се осећати на дан тестирања. Ако знате како да се носите са најтежим питањима која вам тест може поставити, чиниће полагање правог САТ-а много мање застрашујућим.
Ако сте сматрали да су ова питања лака, пазите да не потцењујете ефекат адреналина и умора на вашу способност решавања проблема. Док настављате да учите, увек се придржавајте одговарајућих смерница за време и покушајте да урадите пуне тестове кад год је то могуће. Ово је најбољи начин да поново креирате стварно окружење за тестирање како бисте се могли припремити за прави посао.
Ако сматрате да су ова питања изазовна, обавезно ојачајте своје знање математике тако што ћете погледати наше индивидуалне математичке водиче за САТ. Тамо ћете видети детаљнија објашњења тема о којима је реч, као и детаљније рашчлањивање одговора.
Шта је следеће?
Осетили сте да су ова питања тежа него што сте очекивали? Погледајте све теме обухваћене у САТ одељку из математике, а затим забележите који одељци су вам представљали посебну потешкоћу. Затим погледајте наше индивидуалне математичке водиче који ће вам помоћи да учврстите било коју од тих слабих области.
Понестаје вам времена за САТ математичку секцију? Наш водич ће вам помоћи да победите сат и повећате свој резултат.
Циљате на савршен резултат? Провери наш водич о томе како да добијете савршених 800 на САТ одељку из математике , који је написао савршени стрелац.
,166$ или

Желите да се тестирате против најтежих САТ математичких питања? Желите да знате шта ова питања чини тако тешким и како их најбоље решити? Ако сте спремни да заиста утонете своје зубе у САТ одељак из математике и усредсредите се на савршен резултат, онда је ово водич за вас.
Саставили смо оно што верујемо да јесте 15 најтежих питања за тренутни САТ , са стратегијама и објашњењима одговора за сваки. Ово су све тешка САТ математичка питања са САТ тестова за вежбање Цоллеге Боард-а, што значи да је њихово разумевање један од најбољих начина за учење за оне од вас који теже савршенству.
Слика: Сониа Севилла /Викимедија
Кратак преглед САТ Матх
Трећи и четврти део САТ увек ће бити математички део . Први математички пододељак (означен са '3') ради не омогућавају вам да користите калкулатор, док је други математички пододељак (означен са '4') ради дозволити коришћење калкулатора. Међутим, не брините превише о одељку без калкулатора: ако вам није дозвољено да користите калкулатор за питање, то значи да вам није потребан калкулатор да бисте одговорили на њега.
Сваки математички пододељак је распоређен по растућој тежини (где је дуже потребно да се реши проблем и што мање људи на њега тачно одговори, то је теже). У сваком пододељку, питање 1 ће бити „лако“, а питање 15 ће се сматрати „тешким“. Међутим, растућа потешкоћа се ресетује са лаке на тешку на мрежи.
Дакле, питања са вишеструким избором су распоређена по растућој тежини (питања 1 и 2 ће бити најлакша, питања 14 и 15 ће бити најтежа), али ниво тежине се ресетује за одељак мреже (што значи да ће питања 16 и 17 поново бити 'лако', а питања 19 и 20 ће бити веома тешка).
Уз врло мало изузетака, дакле, најтежи САТ математички задаци ће бити групирани на крају сегмената са вишеструким избором или у другој половини питања у мрежи. Међутим, поред њиховог постављања на тест, ова питања имају и неколико других заједничких карактеристика. За минут ћемо погледати примере питања и како да их решимо, а затим их анализирамо да бисмо открили шта је заједничко овим врстама питања.
Али прво: да ли би требало да се сада фокусирате на најтежа математичка питања?
Ако тек почињете са припремама за учење (или ако сте једноставно прескочили овај први, кључни корак), дефинитивно престаните и урадите потпуни тест да бисте проценили свој тренутни ниво бодова. Погледајте наш водич за сви бесплатни САТ тестови за вежбање доступни на мрежи а затим седите да урадите тест одједном.
Апсолутно најбољи начин да процените свој тренутни ниво је да једноставно урадите САТ тест као да је стваран, држећи стриктно време и радећи директно са само дозвољеним паузама (знамо - вероватно није ваш омиљени начин да проведете суботу). Када стекнете добру представу о свом тренутном нивоу и процентуалном рангирању, можете поставити прекретнице и циљеве за свој коначни резултат САТ математике.
Ако тренутно постижете резултате у распону од 200-400 или 400-600 на САТ математици, најбоље је да прво погледате наш водич за побољшање вашег математичког резултата да стално будете на или преко 600 пре него што почнете да покушавате да се ухватите у коштац са најтежим математичким проблемима на тесту.
Међутим, ако већ постижете више од 600 поена у одељку из математике и желите да тестирате своју снагу за прави САТ, онда свакако пређите на остатак овог водича. Ако тежите савршеном (или близу) , онда ћете морати да знате како изгледају најтежа САТ математичка питања и како да их решите. И на срећу, управо то ћемо и урадити.
УПОЗОРЕЊЕ: Пошто постоји ограничен број званични САТ практични тестови , можда ћете желети да сачекате да прочитате овај чланак док не покушате све или већину прва четири званична теста за вежбање (пошто је већина питања у наставку преузета из тих тестова). Ако сте забринути да не покварите те тестове, престаните сада да читате овај водич; вратите се и прочитајте када их завршите.

Хајде сада да пређемо на нашу листу питања (вхоо)!
Слика: Ниитк /ДевиантАрт
15 најтежих САТ математичких питања
Сада када сте сигурни да би требало да покушате са оваквим питањима, хајде да одмах уђемо! У наставку смо припремили 15 најтежих САТ математичких питања које можете испробати, заједно са упутствима о томе како да добијете одговор (ако сте збуњени).
Нема калкулатора САТ математичких питања
Питање 1
$$Ц=5/9(Ф-32)$$
Горња једначина показује како је температура $Ф$, мерена у степенима Фаренхајта, повезана са температуром $Ц$, мереном у степенима Целзијуса. На основу једначине, шта од следећег мора бити тачно?
- Повећање температуре од 1 степен Фаренхајта је еквивалентно повећању температуре од 5/9$ степени Целзијуса.
- Повећање температуре од 1 степен Целзијуса је еквивалентно повећању температуре од 1,8 степени Фаренхајта.
- Повећање температуре од $5/9$ степени Фаренхајта је еквивалентно порасту температуре од 1 степен Целзијуса.
А) Само ја
Б) Само ИИ
Ц) Само ИИИ
Д) само И и ИИ
ОБЈАШЊЕЊЕ ОДГОВОРА: Замислите једначину као једначину за праву
$$и=мк+б$$
где у овом случају
$$Ц= {5}/{9} (Ф−32)$$
или
$$Ц={5}/{9}Ф −{5}/{9}(32)$$
Можете да видите да је нагиб графика ${5}/{9}$, што значи да је за повећање од 1 степен Фаренхајта повећање износи ${5}/{9}$ од 1 степен Целзијуса.
$$Ц= {5}/{9} (Ф)$$
$$Ц= {5}/{9} (1)= {5}/{9}$$
Дакле, изјава И је тачна. Ово је еквивалентно томе да кажемо да је повећање од 1 степен Целзијуса једнако повећању од ${9}/{5}$ степени Фаренхајта.
$$Ц= {5}/{9} (Ф)$$
$$1= {5}/{9} (Ф)$$
$$(Ф)={9}/{5}$$
Пошто је ${9}/{5}$ = 1,8, изјава ИИ је тачна.
Једини одговор који има и исказ И и исказ ИИ као тачан је Д , али ако имате времена и желите да будете потпуно темељни, такође можете да проверите да ли је изјава ИИИ (повећање од ${5}/{9}$ степен Фаренхајта једнако повећању температуре од 1 степен Целзијуса) тачна :
$$Ц= {5}/{9} (Ф)$$
$$Ц= {5}/{9} ({5}/{9})$$
$$Ц= {25} /{81} (што је = 1)$$
Повећање од $5/9$ степени Фаренхајта доводи до повећања од ${25}/{81}$, а не за 1 степен Целзијуса, тако да изјава ИИИ није тачна.
Коначан одговор је Д.
Питање 2
Једначина${24к^2 + 25к -47}/{ак-2} = -8к-3-{53/{ак-2}}$важи за све вредности $к=2/а$, где је $а$ константа.
Која је вредност $а$?
А) -16
Б) -3
Ц) 3
Д) 16
ОБЈАШЊЕЊЕ ОДГОВОРА: Постоје два начина да се ово питање реши. Бржи начин је да помножите сваку страну дате једначине са $ак-2$ (тако да можете да се ослободите разломка). Када помножите сваку страну са $ак-2$, требало би да имате:
$$24к^2 + 25к - 47 = (-8к-3)(ак-2) - 53$$
Затим би требало да помножите $(-8к-3)$ и $(ак-2)$ користећи ФОИЛ.
$$24к^2 + 25к - 47 = -8ак^2 - 3ак +16к + 6 - 53$$
Затим смањите на десној страни једначине
$$24к^2 + 25к - 47 = -8ак^2 - 3ак +16к - 47$$
Пошто коефицијенти $к^2$-члана морају бити једнаки на обе стране једначине, $−8а = 24$, или $а = −3$.
Друга опција која је дужа и досаднија је да покушате да укључите све изборе одговора за а и видите који избор одговора чини обе стране једначине једнакима. Опет, ово је дужа опција и не препоручујем је за стварни САТ јер ће изгубити превише времена.
Коначни одговор је Б.
Питање 3
Ако је $3к-и = 12$, колика је вредност ${8^к}/{2^и}$?
А) $2^{12}$
Б) $4^4$
Ц) $8^2$
Д) Вредност се не може утврдити из датих информација.
ОБЈАШЊЕЊЕ ОДГОВОРА: Један приступ је изражавање
$${8^к}/{2^и}$$
тако да су бројилац и именилац изражени истом основом. Пошто су 2 и 8 оба степена од 2, замена $2^3$ за 8 у бројиоцу од ${8^к}/{2^и}$ даје
$${(2^3)^к}/{2^и}$$
који се може преписати
$${2^3к}/{2^и}$$
Пошто бројилац и именилац имају заједничку основу, овај израз се може преписати као $2^(3к−и)$. У питању се наводи да је $3к − и = 12$, па се експонент, $3к − и$ може заменити са 12, што значи да
$${8^к}/{2^и}= 2^12$$
Коначан одговор је А.
Питање 4
Тачке А и Б леже на кругу полупречника 1, а лук ${АБ}↖⌢$ има дужину од $π/3$. Колики део обима круга је дужина лука ${АБ}↖⌢$?
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте сазнали одговор на ово питање, прво ћете морати да знате формулу за проналажење обима круга.
Обим, $Ц$, круга је $Ц = 2πр$, где је $р$ полупречник круга. За дати круг полупречника 1, обим је $Ц = 2(π)(1)$, или $Ц = 2π$.
Да бисте сазнали колики је део обима дужине ${АБ}↖⌢$, поделите дужину лука са обимом, што даје $π/3 ÷ 2π$. Ова подела се може представити са $π/3 * {1/2}π = 1/6$.
Разломак $1/6$ се такође може преписати као $0,166$ или $0,167$.
Коначни одговор је $1/6$, $0,166$ или $0,167$.
Питање 5
$${8-и}/{3-2и}$$
Ако се горњи израз препише у облику $а+би$, где су $а$ и $б$ реални бројеви, колика је вредност $а$? (Напомена: $и=√{-1}$)
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте преписали ${8-и}/{3-2и}$ у стандардном облику $а + би$, потребно је да помножите бројилац и именилац од ${8-и}/{3-2и}$ коњугатом , $3 + 2и$. Ово је једнако
$$({8-и}/{3-2и})({3+2и}/{3+2и})={24+16и-3+(-и)(2и)}/{(3^2 )-(2и)^2}$$
Пошто $и^2=-1$, овај последњи разломак се може поједноставити на
$$ {24+16и-3и+2}/{9-(-4)}={26+13и}/{13}$$
што даље поједностављује на $2 + и$. Стога, када се ${8-и}/{3-2и}$ поново напише у стандардном облику а + би, вредност а је 2.
Коначан одговор је А.
Питање 6
У троуглу $АБЦ$, мера $∠Б$ је 90°, $БЦ=16$ и $АЦ$=20. Троугао $ДЕФ$ је сличан троуглу $АБЦ$, где врхови $Д$, $Е$ и $Ф$ одговарају теменима $А$, $Б$ и $Ц$, респективно, и свакој страни троугла $ ДЕФ$ је $1/3$ дужина одговарајуће странице троугла $АБЦ$. Која је вредност $синФ$?
ОБЈАШЊЕЊЕ ОДГОВОРА: Троугао АБЦ је правоугли троугао са правим углом у Б. Према томе, $ов {АЦ}$ је хипотенуза правоуглог троугла АБЦ, а $ов {АБ}$ и $ов {БЦ}$ су катете правоугли троугао АБЦ. Према Питагориној теореми,
$$АБ =√{20^2-16^2}=√{400-256}=√{144}=12$$
Пошто је троугао ДЕФ сличан троуглу АБЦ, са врхом Ф који одговара темену Ц, мера $угла ∠ {Ф}$ једнака је мери $угла ∠ {Ц}$. Дакле, $син Ф = син Ц$. Од дужина страница троугла АБЦ,
$$синФ ={супротно сиде}/{хипотенусе}={АБ}/{АЦ}={12}/{20}={3}/{5}$$
Дакле, $синФ ={3}/{5}$.
Коначни одговор је ${3}/{5}$ или 0,6.
Питања из математике за САТ дозвољена за калкулатор
Питање 7

Непотпуна табела изнад сумира број ученика леворуких и десноруких ученика према полу за ученике осмог разреда средње школе Кеисел. Десноруких ученица има 5 пута више него леворуких, а 9 пута више дешњака него леворуких ученика. ако у школи има укупно 18 леворуких ученика и 122 дешњака, шта је од следећег најближе вероватноћи да је случајно одабран дешњак женског пола? (Напомена: Претпоставимо да ниједан ученик осмог разреда није и дешњак и леворук.)
А) 0,410
Б) 0,357
Ц) 0,333
Д) 0,250
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте решили овај проблем, требало би да направите две једначине користећи две променљиве ($к$ и $и$) и информације које сте добили. Нека је $к$ број леворуких ученица и нека је $и$ број леворуких ученика. Користећи информације дате у задатку, број дешњака ће бити $5к$, а број дешњака ће бити $9и$. Пошто је укупан број леворуких ученика 18, а укупан број дешњака 122, систем једначина испод мора да буде тачан:
$$к + и = 18$$
$$5к + 9и = 122$$
Када решите овај систем једначина, добијате $к = 10$ и $и = 8$. Дакле, 5*10, односно 50, од 122 дешњака су жене. Према томе, вероватноћа да је дешњак изабран насумично женско је ${50}/{122}$, што је на најближи хиљадити део 0,410.
Коначан одговор је А.Питања 8 и 9
Користите следеће информације и за питање 7 и за питање 8.
Ако купци уђу у продавницу просечном брзином од $р$ купаца по минуту и сваки остане у продавници просечно време од $Т$ минута, даје се просечан број купаца у продавници, $Н$, у било ком тренутку по формули $Н=рТ$. Овај однос је познат као Литлов закон.
Власник Гоод Деалс Сторе-а процењује да током радног времена у продавницу уђу у просеку 3 купца у минуту и да се сваки од њих задржава у просеку 15 минута. Власник продавнице користи Литлов закон да процени да у продавници у сваком тренутку има 45 купаца.
Питање 8
Литтлеов закон се може применити на било који део продавнице, као што је одређено одељење или редови на благајни. Власник продавнице утврђује да током радног времена отприлике 84 купца по сату обави куповину и сваки од ових купаца проведе у просеку 5 минута на каси. У било ком тренутку током радног времена, колико отприлике купаца у просеку чека у реду за касу да обави куповину у продавници Гоод Деалс?
ОБЈАШЊЕЊЕ ОДГОВОРА: Пошто питање каже да се Литлов закон може применити на било који део продавнице (на пример, само на ред за одјаву), онда је просечан број купаца, $Н$, у реду за одјаву у било ком тренутку $Н = рТ $, где је $р$ број купаца који улазе у ред за одјаву по минуту, а $Т$ је просечан број минута које сваки купац проведе у реду за плаћање.
Пошто 84 купца на сат обави куповину, 84 купца по сату улази у ред за одјаву. Међутим, ово треба да се конвертује у број купаца у минути (да би се користило са $Т = 5$). Пошто у једном сату има 60 минута, цена је {84 $ купаца по сату}/{60 минута} = 1,4$ купаца по минуту. Коришћење дате формуле са $р = 1.4$ и $Т = 5$ даје принос
$$Н = рт = (1.4)(5) = 7$$
Према томе, просечан број купаца, $Н$, у реду за касу у било ком тренутку током радног времена је 7.
Коначан одговор је 7.
Питање 9
Власник продавнице Гоод Деалс отвара нову продавницу широм града. За нову радњу, власник процењује да ће током радног времена у просеку бити око 90 купаца посатуђу у продавницу и сваки од њих остаје у просеку 12 минута. Просечан број купаца у новој продавници у било ком тренутку је који проценат мањи од просечног броја купаца у оригиналној продавници у било ком тренутку? (Напомена: Занемарите симбол за проценат када уносите свој одговор. На пример, ако је одговор 42,1%, унесите 42,1)
ОБЈАШЊЕЊЕ ОДГОВОРА: Према првобитним информацијама, процењени просечан број купаца у првобитној продавници у било ком тренутку (Н) је 45. У питању се наводи да у новој продавници менаџер процењује да је просечно 90 купаца на сат (60 минута) уђите у продавницу, што је еквивалентно 1,5 купаца у минути (р). Менаџер такође процењује да сваки купац остаје у продавници у просеку 12 минута (Т). Дакле, према Литловом закону, у новој продавници у било ком тренутку има, у просеку, $Н = рТ = (1,5)(12) = 18$ купаца. Ово је
$${45-18}/{45} * 100 = 60$$
проценат мање од просечног броја купаца у оригиналној продавници у било ком тренутку.
Коначан одговор је 60.
Питање 10
У $ки$-равни, тачка $(п,р)$ лежи на правој са једначином $и=к+б$, где је $б$ константа. Тачка са координатама $(2п, 5р)$ лежи на правој са једначином $и=2к+б$. Ако је $п=0$, колика је вредност $р/п$?
А) $2/5$
Б) $3/4$
Ц) $4/3$
Д) $5/2$
ОБЈАШЊЕЊЕ ОДГОВОРА: Пошто тачка $(п,р)$ лежи на правој са једначином $и=к+б$, та тачка мора да задовољи једначину. Замена $п$ за $к$ и $р$ за $и$ у једначини $и=к+б$ даје $р=п+б$, или $би б$ = $би р-би п $.
Слично томе, пошто тачка $(2п,5р)$ лежи на правој са једначином $и=2к+б$, тачка мора да задовољава једначину. Замена $2п$ за $к$ и $5р$ за $и$ у једначини $и=2к+б$ даје:
$5р=2(2п)+б$
$5р=4п+б$
$би б$ = $бо 5 би р-бо 4би п$.
Затим, можемо поставити две једначине једнаке $б$ једна другој и поједноставити:
$б=р-п=5р-4п$
$3п=4р$
Коначно, да бисмо пронашли $р/п$, морамо да поделимо обе стране једначине са $п$ и са $4$:
$3п=4р$
$3={4р}/п$
$3/4=р/п$
Тачан одговор је Б , $3/4$.
Ако сте изабрали изборе А и Д, можда сте погрешно формирали свој одговор од коефицијената у тачки $(2п, 5р)$. Ако сте изабрали избор Ц, можда сте побркали $р$ и $п$.
Имајте на уму да док се ово налази у одељку за калкулатор САТ-а, апсолутно вам није потребан ваш калкулатор да бисте га решили!
Питање 11
 Силос за жито је изграђен од два десна кружна конуса и десног кружног цилиндра са унутрашњим мерама приказаним на слици изнад. Од следећег, који је најближи запремини силоса за зрно, у кубним стопама?
Силос за жито је изграђен од два десна кружна конуса и десног кружног цилиндра са унутрашњим мерама приказаним на слици изнад. Од следећег, који је најближи запремини силоса за зрно, у кубним стопама?
А) 261,8
Б) 785,4
Ц) 916.3
Д) 1047.2
ОБЈАШЊЕЊЕ ОДГОВОРА: Запремина силоса за зрно може се наћи додавањем запремина свих чврстих материја од којих се састоји (цилиндра и два конуса). Силос се састоји од цилиндра (висине 10 стопа и полупречника основе 5 стопа) и два конуса (сваки са висином 5 стопа и полупречником основе 5 стопа). Формуле дате на почетку одељка САТ математике:
Запремина конуса
$$В={1}/{3}πр^2х$$
Запремина цилиндра
$$В=πр^2х$$
може се користити за одређивање укупне запремине силоса. Пошто два конуса имају идентичне димензије, укупна запремина силоса, у кубним стопама, дата је као
$$В_{сило}=π(5^2)(10)+(2)({1}/{3})π(5^2)(5)=({4}/{3})(250 )п$$
што је приближно једнако 1.047,2 кубних стопа.
Коначан одговор је Д.
Питање 12
Ако је $к$ просек (аритметичка средина) од $м$ и $9$, $и$ је просек од $2м$ и $15$, а $з$ је просек од $3м$ и $18$, шта је просек од $к$, $и$ и $з$ у смислу $м$?
А) $м+6$
Б) $м+7$
Ц) 2 милиона долара + 14 долара
Д) 3 милиона долара + 21 долара
ОБЈАШЊЕЊЕ ОДГОВОРА: Пошто је просек (аритметичка средина) два броја једнак збиру два броја подељен са 2, једначине $к={м+9}/{2}$, $и={2м+15}/{2 }$, $з={3м+18}/{2}$ су тачне. Просек за $к$, $и$ и $з$ је дат са ${к + и + з}/{3}$. Замена израза у м за сваку променљиву ($к$, $и$, $з$) даје
$$[{м+9}/{2}+{2м+15}/{2}+{3м+18}/{2}]/3$$
Овај разломак се може поједноставити на $м + 7$.
Коначни одговор је Б.
Питање 13
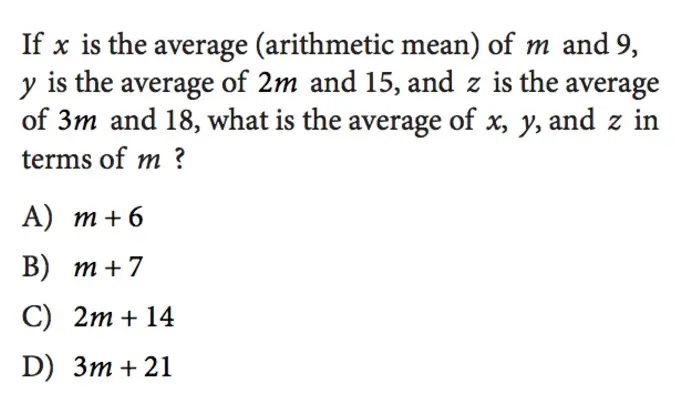
Функција $ф(к)=к^3-к^2-к-{11/4}$ је графички приказана у горњој $ки$-равни. Ако је $к$ константа таква да једначина $ф(к)=к$ има три реална решења, које од следећег може бити вредност $к$?
ОБЈАШЊЕЊЕ ОДГОВОРА: Једначина $ф(к) = к$ даје решења система једначина
$$и = ф(к) = к^3-к^2-к-{11}/{4}$$
и
$$и = к$$
Реално решење система две једначине одговара тачки пресека графика двеју једначина у $ки$-равни.
График $и = к$ је хоризонтална линија која садржи тачку $(0, к)$ и три пута сече график кубичне једначине (пошто има три реална решења). С обзиром на график, једина хоризонтална линија која би три пута пресекла кубну једначину је линија са једначином $и = −3$, или $ф(к) = −3$. Дакле, $к$ је $-3$.
Коначан одговор је Д.
Питање 14
$$к={1/2}нв^2$$
Динамички притисак $к$ генерисан флуидом који се креће брзином $в$ може се наћи коришћењем формуле изнад, где је $н$ константна густина течности. Аеронаутички инжењер користи формулу да пронађе динамички притисак флуида који се креће брзином $в$ и исте течности која се креће брзином 1,5$в$. Колики је однос динамичког притиска бржег флуида и динамичког притиска спорије течности?
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте решили овај проблем, потребно је да поставите једначине са променљивим. Нека је $к_1$ динамички притисак спорије течности која се креће брзином $в_1$, а нека је $к_2$ динамички притисак брже течности која се креће брзином $в_2$. Онда
$$в_2 =1,5в_1$$
Узимајући у обзир једначину $к = {1}/{2}нв^2$, замена динамичког притиска и брзине бржег флуида даје $к_2 = {1}/{2}н(в_2)^2$. Пошто је $в_2 =1.5в_1$, израз $1.5в_1$ може бити замењен са $в_2$ у овој једначини, дајући $к_2 = {1}/{2}н(1.5в_1)^2$. Узимајући на квадрат $1,5$, можете преписати претходну једначину као
$$к_2 = (2.25)({1}/{2})н(в_1)^2 = (2.25)к_1$$
Дакле, однос динамичког притиска бржег флуида је
$${к2}/{к1} = {2,25 к_1}/{к_1}= 2,25 $$
Коначан одговор је 2,25 или 9/4.
Питање 15
За полином $п(к)$, вредност $п(3)$ је $-2$. Шта од следећег мора бити тачно за $п(к)$?
А) $к-5$ је фактор од $п(к)$.
Б) $к-2$ је фактор од $п(к)$.
Ц) $к+2$ је фактор од $п(к)$.
Д) Остатак када се $п(к)$ подели са $к-3$ је $-2$.
ОБЈАШЊЕЊЕ ОДГОВОРА: Ако је полином $п(к)$ подељен полиномом облика $к+к$ (који обухвата све могуће изборе одговора у овом питању), резултат се може написати као
$${п(к)}/{к+к}=к(к)+{р}/{к+к}$$
где је $к(к)$ полином, а $р$ остатак. Пошто је $к + к$ полином степена 1 (што значи да укључује само $к^1$ и нема виших експонента), остатак је реалан број.
Према томе, $п(к)$ се може преписати као $п(к) = (к + к)к(к) + р$, где је $р$ реалан број.
Питање гласи да је $п(3) = -2$, тако да мора бити тачно да
$$-2 = п(3) = (3 + к)к(3) + р$$
Сада можемо укључити све могуће одговоре. Ако је одговор А, Б или Ц, $р$ ће бити $0$, док ако је одговор Д, $р$ ће бити $-2$.
А. $-2 = п(3) = (3 + (-5))к(3) + 0$
$-2=(3-5)к(3)$
$-2=(-2)к(3)$
Ово би могло бити тачно, али само ако је $к(3)=1$
Б. $-2 = п(3) = (3 + (-2))к(3) + 0$
$-2 = (3-2)к(3)$
$-2 = (-1)к(3)$
Ово би могло бити тачно, али само ако је $к(3)=2$
Ц. $-2 = п(3) = (3 + 2)к(3) + 0$
$-2 = (5)к(3)$
Ово би могло бити тачно, али само ако је $к(3)={-2}/{5}$
Д. $-2 = п(3) = (3 + (-3))к(3) + (-2)$
$-2 = (3 - 3)к(3) + (-2)$
$-2 = (0)к(3) + (-2)$
Ово ће увек буди истинит без обзира шта је $к(3)$.
Од избора одговора, једини који мора ако је тачно да је $п(к)$ Д, да је остатак када се $п(к)$ подели са $к-3$ -2.
Коначан одговор је Д.

Заслужујеш све дремке након што прођеш кроз та питања.
Шта је заједничко најтежим САТ математичким питањима?
Важно је разумети шта ова тешка питања чини „тешким“. На тај начин ћете моћи да разумете и решите слична питања када их видите на дан тестирања, као и да имате бољу стратегију за идентификацију и исправљање ваших претходних САТ математичких грешака.
У овом одељку ћемо погледати шта ова питања имају заједничко и дати примере сваке врсте. Неки од разлога зашто су најтежа математичка питања најтежа математичка питања су:
#1: Тестирајте неколико математичких концепата одједном

Овде морамо да се бавимо замишљеним бројевима и разломцима одједном.
Тајна успеха: Размислите коју применљиву математику можете користити да решите проблем, радите корак по корак и испробајте сваку технику док не пронађете ону која функционише!
#2: Укључује много корака
Запамтите: што више корака треба да предузмете, лакше ћете забрљати негде на линији!
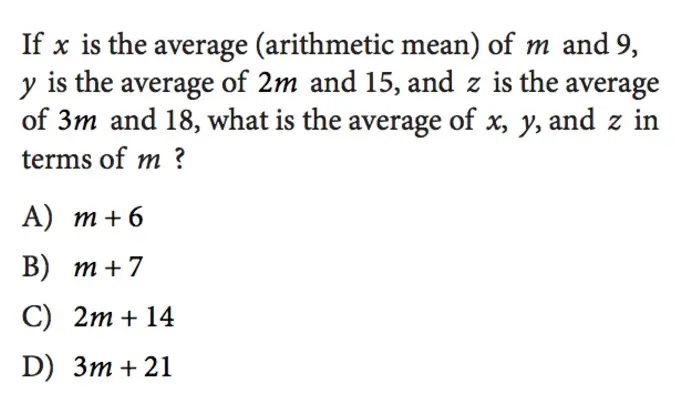
Морамо да решимо овај проблем у корацима (радећи неколико просека) да бисмо откључали остатак одговора у домино ефекту. Ово може бити збуњујуће, посебно ако сте под стресом или вам понестаје времена.
Тајна успеха: Полако, идите корак по корак и још једном проверите свој рад како не бисте погрешили!
#3: Тестирајте концепте са којима сте ограничено упознати
На пример, многи ученици су мање упознати са функцијама него са разломцима и процентима, тако да се већина функционалних питања сматра проблемима „високе тежине“.

Ако не знате како се сналазите у функцијама, ово би био тежак проблем.
Тајна успеха: Прегледајте математичке концепте са којима нисте толико упознати, као што су функције. Предлажемо да користите наше сјајне бесплатне САТ Матх водиче за преглед.
#4: Написане су на необичне или замршене начине
Може бити тешко схватити која су тачно нека питања питајући , а још мање схватити како их решити. Ово је посебно тачно када се питање налази на крају одељка, а понестаје вам времена.

Пошто ово питање пружа толико информација без дијаграма, може бити тешко загонетнути у ограниченом дозвољеном времену.
Тајна успеха: Узмите си времена, анализирајте шта се од вас тражи и нацртајте дијаграм ако вам је од помоћи.
#5: Користите много различитих варијабли

Са толико различитих варијабли у игри, прилично је лако доћи до забуне.
Тајна успеха: Узмите си времена, анализирајте шта се од вас тражи и размислите да ли је додавање бројева добра стратегија за решавање проблема (то не би било за горње питање, али би било за многа друга питања о променљивој САТ).
Тхе Таке-Аваис
САТ је маратон и што сте боље припремљени за њега, боље ћете се осећати на дан тестирања. Ако знате како да се носите са најтежим питањима која вам тест може поставити, чиниће полагање правог САТ-а много мање застрашујућим.
Ако сте сматрали да су ова питања лака, пазите да не потцењујете ефекат адреналина и умора на вашу способност решавања проблема. Док настављате да учите, увек се придржавајте одговарајућих смерница за време и покушајте да урадите пуне тестове кад год је то могуће. Ово је најбољи начин да поново креирате стварно окружење за тестирање како бисте се могли припремити за прави посао.
Ако сматрате да су ова питања изазовна, обавезно ојачајте своје знање математике тако што ћете погледати наше индивидуалне математичке водиче за САТ. Тамо ћете видети детаљнија објашњења тема о којима је реч, као и детаљније рашчлањивање одговора.
Шта је следеће?
Осетили сте да су ова питања тежа него што сте очекивали? Погледајте све теме обухваћене у САТ одељку из математике, а затим забележите који одељци су вам представљали посебну потешкоћу. Затим погледајте наше индивидуалне математичке водиче који ће вам помоћи да учврстите било коју од тих слабих области.
Понестаје вам времена за САТ математичку секцију? Наш водич ће вам помоћи да победите сат и повећате свој резултат.
Циљате на савршен резултат? Провери наш водич о томе како да добијете савршених 800 на САТ одељку из математике , који је написао савршени стрелац.
,167$.
Питање 5
$${8-и}/{3-2и}$$
Ако се горњи израз препише у облику $а+би$, где су $а$ и $б$ реални бројеви, колика је вредност $а$? (Напомена: $и=√{-1}$)
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте преписали ${8-и}/{3-2и}$ у стандардном облику $а + би$, потребно је да помножите бројилац и именилац од ${8-и}/{3-2и}$ коњугатом , + 2и$. Ово је једнако
$$({8-и}/{3-2и})({3+2и}/{3+2и})={24+16и-3+(-и)(2и)}/{(3^2 )-(2и)^2}$$
Пошто $и^2=-1$, овај последњи разломак се може поједноставити на
$$ {24+16и-3и+2}/{9-(-4)}={26+13и}/{13}$$
реацтјс мап
што даље поједностављује на + и$. Стога, када се ${8-и}/{3-2и}$ поново напише у стандардном облику а + би, вредност а је 2.
Коначан одговор је А.
Питање 6
У троуглу $АБЦ$, мера $∠Б$ је 90°, $БЦ=16$ и $АЦ$=20. Троугао $ДЕФ$ је сличан троуглу $АБЦ$, где врхови $Д$, $Е$ и $Ф$ одговарају теменима $А$, $Б$ и $Ц$, респективно, и свакој страни троугла $ ДЕФ$ је /3$ дужина одговарајуће странице троугла $АБЦ$. Која је вредност $синФ$?
ОБЈАШЊЕЊЕ ОДГОВОРА: Троугао АБЦ је правоугли троугао са правим углом у Б. Према томе, $ов {АЦ}$ је хипотенуза правоуглог троугла АБЦ, а $ов {АБ}$ и $ов {БЦ}$ су катете правоугли троугао АБЦ. Према Питагориној теореми,
$$АБ =√{20^2-16^2}=√{400-256}=√{144}=12$$
Пошто је троугао ДЕФ сличан троуглу АБЦ, са врхом Ф који одговара темену Ц, мера $угла ∠ {Ф}$ једнака је мери $угла ∠ {Ц}$. Дакле, $син Ф = син Ц$. Од дужина страница троугла АБЦ,
$$синФ ={супротно сиде}/{хипотенусе}={АБ}/{АЦ}={12}/{20}={3}/{5}$$
Дакле, $синФ ={3}/{5}$.
Коначни одговор је /{5}$ или 0,6.
Питања из математике за САТ дозвољена за калкулатор
Питање 7

Непотпуна табела изнад сумира број ученика леворуких и десноруких ученика према полу за ученике осмог разреда средње школе Кеисел. Десноруких ученица има 5 пута више него леворуких, а 9 пута више дешњака него леворуких ученика. ако у школи има укупно 18 леворуких ученика и 122 дешњака, шта је од следећег најближе вероватноћи да је случајно одабран дешњак женског пола? (Напомена: Претпоставимо да ниједан ученик осмог разреда није и дешњак и леворук.)
А) 0,410
Б) 0,357
Ц) 0,333
Д) 0,250
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте решили овај проблем, требало би да направите две једначине користећи две променљиве ($к$ и $и$) и информације које сте добили. Нека је $к$ број леворуких ученица и нека је $и$ број леворуких ученика. Користећи информације дате у задатку, број дешњака ће бити к$, а број дешњака ће бити и$. Пошто је укупан број леворуких ученика 18, а укупан број дешњака 122, систем једначина испод мора да буде тачан:
$$к + и = 18$$
$к + 9и = 122$$
Када решите овај систем једначина, добијате $к = 10$ и $и = 8$. Дакле, 5*10, односно 50, од 122 дешњака су жене. Према томе, вероватноћа да је дешњак изабран насумично женско је /{122}$, што је на најближи хиљадити део 0,410.
Коначан одговор је А.
Питања 8 и 9
Користите следеће информације и за питање 7 и за питање 8.
Ако купци уђу у продавницу просечном брзином од $р$ купаца по минуту и сваки остане у продавници просечно време од $Т$ минута, даје се просечан број купаца у продавници, $Н$, у било ком тренутку по формули $Н=рТ$. Овај однос је познат као Литлов закон.
Власник Гоод Деалс Сторе-а процењује да током радног времена у продавницу уђу у просеку 3 купца у минуту и да се сваки од њих задржава у просеку 15 минута. Власник продавнице користи Литлов закон да процени да у продавници у сваком тренутку има 45 купаца.
Питање 8
Литтлеов закон се може применити на било који део продавнице, као што је одређено одељење или редови на благајни. Власник продавнице утврђује да током радног времена отприлике 84 купца по сату обави куповину и сваки од ових купаца проведе у просеку 5 минута на каси. У било ком тренутку током радног времена, колико отприлике купаца у просеку чека у реду за касу да обави куповину у продавници Гоод Деалс?
ОБЈАШЊЕЊЕ ОДГОВОРА: Пошто питање каже да се Литлов закон може применити на било који део продавнице (на пример, само на ред за одјаву), онда је просечан број купаца, $Н$, у реду за одјаву у било ком тренутку $Н = рТ $, где је $р$ број купаца који улазе у ред за одјаву по минуту, а $Т$ је просечан број минута које сваки купац проведе у реду за плаћање.
Пошто 84 купца на сат обави куповину, 84 купца по сату улази у ред за одјаву. Међутим, ово треба да се конвертује у број купаца у минути (да би се користило са $Т = 5$). Пошто у једном сату има 60 минута, цена је {84 $ купаца по сату}/{60 минута} = 1,4$ купаца по минуту. Коришћење дате формуле са $р = 1.4$ и $Т = 5$ даје принос
$$Н = рт = (1.4)(5) = 7$$
Према томе, просечан број купаца, $Н$, у реду за касу у било ком тренутку током радног времена је 7.
Коначан одговор је 7.
Питање 9
Власник продавнице Гоод Деалс отвара нову продавницу широм града. За нову радњу, власник процењује да ће током радног времена у просеку бити око 90 купаца посатуђу у продавницу и сваки од њих остаје у просеку 12 минута. Просечан број купаца у новој продавници у било ком тренутку је који проценат мањи од просечног броја купаца у оригиналној продавници у било ком тренутку? (Напомена: Занемарите симбол за проценат када уносите свој одговор. На пример, ако је одговор 42,1%, унесите 42,1)
ОБЈАШЊЕЊЕ ОДГОВОРА: Према првобитним информацијама, процењени просечан број купаца у првобитној продавници у било ком тренутку (Н) је 45. У питању се наводи да у новој продавници менаџер процењује да је просечно 90 купаца на сат (60 минута) уђите у продавницу, што је еквивалентно 1,5 купаца у минути (р). Менаџер такође процењује да сваки купац остаје у продавници у просеку 12 минута (Т). Дакле, према Литловом закону, у новој продавници у било ком тренутку има, у просеку, $Н = рТ = (1,5)(12) = 18$ купаца. Ово је
$${45-18}/{45} * 100 = 60$$
цсс болд
проценат мање од просечног броја купаца у оригиналној продавници у било ком тренутку.
Коначан одговор је 60.
Питање 10
У $ки$-равни, тачка $(п,р)$ лежи на правој са једначином $и=к+б$, где је $б$ константа. Тачка са координатама $(2п, 5р)$ лежи на правој са једначином $и=2к+б$. Ако је $п=0$, колика је вредност $р/п$?
А) /5$
Б) /4$
Ц) /3$
Д) /2$
ОБЈАШЊЕЊЕ ОДГОВОРА: Пошто тачка $(п,р)$ лежи на правој са једначином $и=к+б$, та тачка мора да задовољи једначину. Замена $п$ за $к$ и $р$ за $и$ у једначини $и=к+б$ даје $р=п+б$, или $би б$ = $би р-би п $.
Слично томе, пошто тачка $(2п,5р)$ лежи на правој са једначином $и=2к+б$, тачка мора да задовољава једначину. Замена п$ за $к$ и р$ за $и$ у једначини $и=2к+б$ даје:
р=2(2п)+б$
р=4п+б$
$би б$ = $бо 5 би р-бо 4би п$.
Затим, можемо поставити две једначине једнаке $б$ једна другој и поједноставити:
$б=р-п=5р-4п$
п=4р$
Коначно, да бисмо пронашли $р/п$, морамо да поделимо обе стране једначине са $п$ и са $:
п=4р$
={4р}/п$
/4=р/п$
Тачан одговор је Б , /4$.
Ако сте изабрали изборе А и Д, можда сте погрешно формирали свој одговор од коефицијената у тачки $(2п, 5р)$. Ако сте изабрали избор Ц, можда сте побркали $р$ и $п$.
Имајте на уму да док се ово налази у одељку за калкулатор САТ-а, апсолутно вам није потребан ваш калкулатор да бисте га решили!
Питање 11
 Силос за жито је изграђен од два десна кружна конуса и десног кружног цилиндра са унутрашњим мерама приказаним на слици изнад. Од следећег, који је најближи запремини силоса за зрно, у кубним стопама?
Силос за жито је изграђен од два десна кружна конуса и десног кружног цилиндра са унутрашњим мерама приказаним на слици изнад. Од следећег, који је најближи запремини силоса за зрно, у кубним стопама?
А) 261,8
Б) 785,4
Ц) 916.3
Д) 1047.2
ОБЈАШЊЕЊЕ ОДГОВОРА: Запремина силоса за зрно може се наћи додавањем запремина свих чврстих материја од којих се састоји (цилиндра и два конуса). Силос се састоји од цилиндра (висине 10 стопа и полупречника основе 5 стопа) и два конуса (сваки са висином 5 стопа и полупречником основе 5 стопа). Формуле дате на почетку одељка САТ математике:
Запремина конуса
$$В={1}/{3}πр^2х$$
Запремина цилиндра
$$В=πр^2х$$
може се користити за одређивање укупне запремине силоса. Пошто два конуса имају идентичне димензије, укупна запремина силоса, у кубним стопама, дата је као
$$В_{сило}=π(5^2)(10)+(2)({1}/{3})π(5^2)(5)=({4}/{3})(250 )п$$
што је приближно једнако 1.047,2 кубних стопа.
Коначан одговор је Д.
Питање 12
Ако је $к$ просек (аритметичка средина) од $м$ и $, $и$ је просек од м$ и $, а $з$ је просек од м$ и $, шта је просек од $к$, $и$ и $з$ у смислу $м$?
А) $м+6$
Б) $м+7$
Ц) 2 милиона долара + 14 долара
Д) 3 милиона долара + 21 долара
ОБЈАШЊЕЊЕ ОДГОВОРА: Пошто је просек (аритметичка средина) два броја једнак збиру два броја подељен са 2, једначине $к={м+9}/{2}$, $и={2м+15}/{2 }$, $з={3м+18}/{2}$ су тачне. Просек за $к$, $и$ и $з$ је дат са ${к + и + з}/{3}$. Замена израза у м за сваку променљиву ($к$, $и$, $з$) даје
$$[{м+9}/{2}+{2м+15}/{2}+{3м+18}/{2}]/3$$
Овај разломак се може поједноставити на $м + 7$.
Коначни одговор је Б.
Питање 13
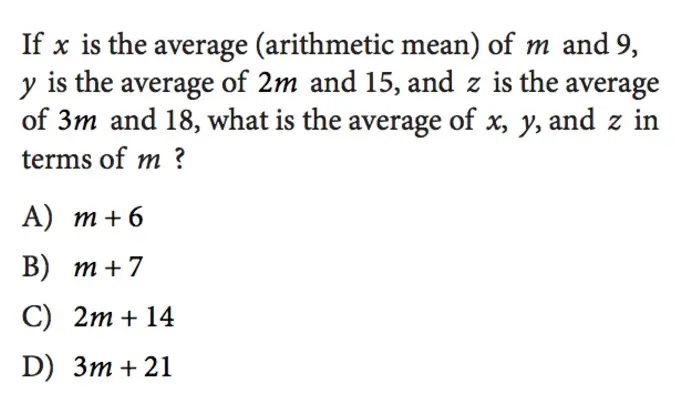
Функција $ф(к)=к^3-к^2-к-{11/4}$ је графички приказана у горњој $ки$-равни. Ако је $к$ константа таква да једначина $ф(к)=к$ има три реална решења, које од следећег може бити вредност $к$?
ОБЈАШЊЕЊЕ ОДГОВОРА: Једначина $ф(к) = к$ даје решења система једначина
$$и = ф(к) = к^3-к^2-к-{11}/{4}$$
и
$$и = к$$
Реално решење система две једначине одговара тачки пресека графика двеју једначина у $ки$-равни.
График $и = к$ је хоризонтална линија која садржи тачку $(0, к)$ и три пута сече график кубичне једначине (пошто има три реална решења). С обзиром на график, једина хоризонтална линија која би три пута пресекла кубну једначину је линија са једначином $и = −3$, или $ф(к) = −3$. Дакле, $к$ је $-3$.
Коначан одговор је Д.
Питање 14
$$к={1/2}нв^2$$
Динамички притисак $к$ генерисан флуидом који се креће брзином $в$ може се наћи коришћењем формуле изнад, где је $н$ константна густина течности. Аеронаутички инжењер користи формулу да пронађе динамички притисак флуида који се креће брзином $в$ и исте течности која се креће брзином 1,5$в$. Колики је однос динамичког притиска бржег флуида и динамичког притиска спорије течности?
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте решили овај проблем, потребно је да поставите једначине са променљивим. Нека је $к_1$ динамички притисак спорије течности која се креће брзином $в_1$, а нека је $к_2$ динамички притисак брже течности која се креће брзином $в_2$. Онда
$$в_2 =1,5в_1$$
Узимајући у обзир једначину $к = {1}/{2}нв^2$, замена динамичког притиска и брзине бржег флуида даје $к_2 = {1}/{2}н(в_2)^2$. Пошто је $в_2 =1.5в_1$, израз .5в_1$ може бити замењен са $в_2$ у овој једначини, дајући $к_2 = {1}/{2}н(1.5в_1)^2$. Узимајући на квадрат ,5$, можете преписати претходну једначину као
$$к_2 = (2.25)({1}/{2})н(в_1)^2 = (2.25)к_1$$
Дакле, однос динамичког притиска бржег флуида је
$${к2}/{к1} = {2,25 к_1}/{к_1}= 2,25 $$
Коначан одговор је 2,25 или 9/4.
Питање 15
За полином $п(к)$, вредност $п(3)$ је $-2$. Шта од следећег мора бити тачно за $п(к)$?
А) $к-5$ је фактор од $п(к)$.
Б) $к-2$ је фактор од $п(к)$.
Ц) $к+2$ је фактор од $п(к)$.
Д) Остатак када се $п(к)$ подели са $к-3$ је $-2$.
ОБЈАШЊЕЊЕ ОДГОВОРА: Ако је полином $п(к)$ подељен полиномом облика $к+к$ (који обухвата све могуће изборе одговора у овом питању), резултат се може написати као
$${п(к)}/{к+к}=к(к)+{р}/{к+к}$$
где је $к(к)$ полином, а $р$ остатак. Пошто је $к + к$ полином степена 1 (што значи да укључује само $к^1$ и нема виших експонента), остатак је реалан број.
Према томе, $п(к)$ се може преписати као $п(к) = (к + к)к(к) + р$, где је $р$ реалан број.
Питање гласи да је $п(3) = -2$, тако да мора бити тачно да
$$-2 = п(3) = (3 + к)к(3) + р$$
Сада можемо укључити све могуће одговоре. Ако је одговор А, Б или Ц, $р$ ће бити 
Желите да се тестирате против најтежих САТ математичких питања? Желите да знате шта ова питања чини тако тешким и како их најбоље решити? Ако сте спремни да заиста утонете своје зубе у САТ одељак из математике и усредсредите се на савршен резултат, онда је ово водич за вас.
Саставили смо оно што верујемо да јесте 15 најтежих питања за тренутни САТ , са стратегијама и објашњењима одговора за сваки. Ово су све тешка САТ математичка питања са САТ тестова за вежбање Цоллеге Боард-а, што значи да је њихово разумевање један од најбољих начина за учење за оне од вас који теже савршенству.
Слика: Сониа Севилла /Викимедија
Кратак преглед САТ Матх
Трећи и четврти део САТ увек ће бити математички део . Први математички пододељак (означен са '3') ради не омогућавају вам да користите калкулатор, док је други математички пододељак (означен са '4') ради дозволити коришћење калкулатора. Међутим, не брините превише о одељку без калкулатора: ако вам није дозвољено да користите калкулатор за питање, то значи да вам није потребан калкулатор да бисте одговорили на њега.
Сваки математички пододељак је распоређен по растућој тежини (где је дуже потребно да се реши проблем и што мање људи на њега тачно одговори, то је теже). У сваком пододељку, питање 1 ће бити „лако“, а питање 15 ће се сматрати „тешким“. Међутим, растућа потешкоћа се ресетује са лаке на тешку на мрежи.
Дакле, питања са вишеструким избором су распоређена по растућој тежини (питања 1 и 2 ће бити најлакша, питања 14 и 15 ће бити најтежа), али ниво тежине се ресетује за одељак мреже (што значи да ће питања 16 и 17 поново бити 'лако', а питања 19 и 20 ће бити веома тешка).
Уз врло мало изузетака, дакле, најтежи САТ математички задаци ће бити групирани на крају сегмената са вишеструким избором или у другој половини питања у мрежи. Међутим, поред њиховог постављања на тест, ова питања имају и неколико других заједничких карактеристика. За минут ћемо погледати примере питања и како да их решимо, а затим их анализирамо да бисмо открили шта је заједничко овим врстама питања.
Али прво: да ли би требало да се сада фокусирате на најтежа математичка питања?
Ако тек почињете са припремама за учење (или ако сте једноставно прескочили овај први, кључни корак), дефинитивно престаните и урадите потпуни тест да бисте проценили свој тренутни ниво бодова. Погледајте наш водич за сви бесплатни САТ тестови за вежбање доступни на мрежи а затим седите да урадите тест одједном.
Апсолутно најбољи начин да процените свој тренутни ниво је да једноставно урадите САТ тест као да је стваран, држећи стриктно време и радећи директно са само дозвољеним паузама (знамо - вероватно није ваш омиљени начин да проведете суботу). Када стекнете добру представу о свом тренутном нивоу и процентуалном рангирању, можете поставити прекретнице и циљеве за свој коначни резултат САТ математике.
Ако тренутно постижете резултате у распону од 200-400 или 400-600 на САТ математици, најбоље је да прво погледате наш водич за побољшање вашег математичког резултата да стално будете на или преко 600 пре него што почнете да покушавате да се ухватите у коштац са најтежим математичким проблемима на тесту.
Међутим, ако већ постижете више од 600 поена у одељку из математике и желите да тестирате своју снагу за прави САТ, онда свакако пређите на остатак овог водича. Ако тежите савршеном (или близу) , онда ћете морати да знате како изгледају најтежа САТ математичка питања и како да их решите. И на срећу, управо то ћемо и урадити.
УПОЗОРЕЊЕ: Пошто постоји ограничен број званични САТ практични тестови , можда ћете желети да сачекате да прочитате овај чланак док не покушате све или већину прва четири званична теста за вежбање (пошто је већина питања у наставку преузета из тих тестова). Ако сте забринути да не покварите те тестове, престаните сада да читате овај водич; вратите се и прочитајте када их завршите.

Хајде сада да пређемо на нашу листу питања (вхоо)!
Слика: Ниитк /ДевиантАрт
15 најтежих САТ математичких питања
Сада када сте сигурни да би требало да покушате са оваквим питањима, хајде да одмах уђемо! У наставку смо припремили 15 најтежих САТ математичких питања које можете испробати, заједно са упутствима о томе како да добијете одговор (ако сте збуњени).
Нема калкулатора САТ математичких питања
Питање 1
$$Ц=5/9(Ф-32)$$
Горња једначина показује како је температура $Ф$, мерена у степенима Фаренхајта, повезана са температуром $Ц$, мереном у степенима Целзијуса. На основу једначине, шта од следећег мора бити тачно?
- Повећање температуре од 1 степен Фаренхајта је еквивалентно повећању температуре од 5/9$ степени Целзијуса.
- Повећање температуре од 1 степен Целзијуса је еквивалентно повећању температуре од 1,8 степени Фаренхајта.
- Повећање температуре од $5/9$ степени Фаренхајта је еквивалентно порасту температуре од 1 степен Целзијуса.
А) Само ја
Б) Само ИИ
Ц) Само ИИИ
Д) само И и ИИ
ОБЈАШЊЕЊЕ ОДГОВОРА: Замислите једначину као једначину за праву
$$и=мк+б$$
где у овом случају
$$Ц= {5}/{9} (Ф−32)$$
или
$$Ц={5}/{9}Ф −{5}/{9}(32)$$
Можете да видите да је нагиб графика ${5}/{9}$, што значи да је за повећање од 1 степен Фаренхајта повећање износи ${5}/{9}$ од 1 степен Целзијуса.
$$Ц= {5}/{9} (Ф)$$
$$Ц= {5}/{9} (1)= {5}/{9}$$
Дакле, изјава И је тачна. Ово је еквивалентно томе да кажемо да је повећање од 1 степен Целзијуса једнако повећању од ${9}/{5}$ степени Фаренхајта.
$$Ц= {5}/{9} (Ф)$$
$$1= {5}/{9} (Ф)$$
$$(Ф)={9}/{5}$$
Пошто је ${9}/{5}$ = 1,8, изјава ИИ је тачна.
Једини одговор који има и исказ И и исказ ИИ као тачан је Д , али ако имате времена и желите да будете потпуно темељни, такође можете да проверите да ли је изјава ИИИ (повећање од ${5}/{9}$ степен Фаренхајта једнако повећању температуре од 1 степен Целзијуса) тачна :
$$Ц= {5}/{9} (Ф)$$
$$Ц= {5}/{9} ({5}/{9})$$
$$Ц= {25} /{81} (што је = 1)$$
Повећање од $5/9$ степени Фаренхајта доводи до повећања од ${25}/{81}$, а не за 1 степен Целзијуса, тако да изјава ИИИ није тачна.
Коначан одговор је Д.
Питање 2
Једначина${24к^2 + 25к -47}/{ак-2} = -8к-3-{53/{ак-2}}$важи за све вредности $к=2/а$, где је $а$ константа.
Која је вредност $а$?
А) -16
Б) -3
Ц) 3
Д) 16
ОБЈАШЊЕЊЕ ОДГОВОРА: Постоје два начина да се ово питање реши. Бржи начин је да помножите сваку страну дате једначине са $ак-2$ (тако да можете да се ослободите разломка). Када помножите сваку страну са $ак-2$, требало би да имате:
$$24к^2 + 25к - 47 = (-8к-3)(ак-2) - 53$$
Затим би требало да помножите $(-8к-3)$ и $(ак-2)$ користећи ФОИЛ.
$$24к^2 + 25к - 47 = -8ак^2 - 3ак +16к + 6 - 53$$
Затим смањите на десној страни једначине
$$24к^2 + 25к - 47 = -8ак^2 - 3ак +16к - 47$$
Пошто коефицијенти $к^2$-члана морају бити једнаки на обе стране једначине, $−8а = 24$, или $а = −3$.
Друга опција која је дужа и досаднија је да покушате да укључите све изборе одговора за а и видите који избор одговора чини обе стране једначине једнакима. Опет, ово је дужа опција и не препоручујем је за стварни САТ јер ће изгубити превише времена.
Коначни одговор је Б.
Питање 3
Ако је $3к-и = 12$, колика је вредност ${8^к}/{2^и}$?
А) $2^{12}$
Б) $4^4$
Ц) $8^2$
Д) Вредност се не може утврдити из датих информација.
ОБЈАШЊЕЊЕ ОДГОВОРА: Један приступ је изражавање
$${8^к}/{2^и}$$
тако да су бројилац и именилац изражени истом основом. Пошто су 2 и 8 оба степена од 2, замена $2^3$ за 8 у бројиоцу од ${8^к}/{2^и}$ даје
$${(2^3)^к}/{2^и}$$
који се може преписати
$${2^3к}/{2^и}$$
Пошто бројилац и именилац имају заједничку основу, овај израз се може преписати као $2^(3к−и)$. У питању се наводи да је $3к − и = 12$, па се експонент, $3к − и$ може заменити са 12, што значи да
$${8^к}/{2^и}= 2^12$$
Коначан одговор је А.
Питање 4
Тачке А и Б леже на кругу полупречника 1, а лук ${АБ}↖⌢$ има дужину од $π/3$. Колики део обима круга је дужина лука ${АБ}↖⌢$?
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте сазнали одговор на ово питање, прво ћете морати да знате формулу за проналажење обима круга.
Обим, $Ц$, круга је $Ц = 2πр$, где је $р$ полупречник круга. За дати круг полупречника 1, обим је $Ц = 2(π)(1)$, или $Ц = 2π$.
Да бисте сазнали колики је део обима дужине ${АБ}↖⌢$, поделите дужину лука са обимом, што даје $π/3 ÷ 2π$. Ова подела се може представити са $π/3 * {1/2}π = 1/6$.
Разломак $1/6$ се такође може преписати као $0,166$ или $0,167$.
Коначни одговор је $1/6$, $0,166$ или $0,167$.
Питање 5
$${8-и}/{3-2и}$$
Ако се горњи израз препише у облику $а+би$, где су $а$ и $б$ реални бројеви, колика је вредност $а$? (Напомена: $и=√{-1}$)
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте преписали ${8-и}/{3-2и}$ у стандардном облику $а + би$, потребно је да помножите бројилац и именилац од ${8-и}/{3-2и}$ коњугатом , $3 + 2и$. Ово је једнако
$$({8-и}/{3-2и})({3+2и}/{3+2и})={24+16и-3+(-и)(2и)}/{(3^2 )-(2и)^2}$$
Пошто $и^2=-1$, овај последњи разломак се може поједноставити на
$$ {24+16и-3и+2}/{9-(-4)}={26+13и}/{13}$$
што даље поједностављује на $2 + и$. Стога, када се ${8-и}/{3-2и}$ поново напише у стандардном облику а + би, вредност а је 2.
Коначан одговор је А.
Питање 6
У троуглу $АБЦ$, мера $∠Б$ је 90°, $БЦ=16$ и $АЦ$=20. Троугао $ДЕФ$ је сличан троуглу $АБЦ$, где врхови $Д$, $Е$ и $Ф$ одговарају теменима $А$, $Б$ и $Ц$, респективно, и свакој страни троугла $ ДЕФ$ је $1/3$ дужина одговарајуће странице троугла $АБЦ$. Која је вредност $синФ$?
ОБЈАШЊЕЊЕ ОДГОВОРА: Троугао АБЦ је правоугли троугао са правим углом у Б. Према томе, $ов {АЦ}$ је хипотенуза правоуглог троугла АБЦ, а $ов {АБ}$ и $ов {БЦ}$ су катете правоугли троугао АБЦ. Према Питагориној теореми,
$$АБ =√{20^2-16^2}=√{400-256}=√{144}=12$$
Пошто је троугао ДЕФ сличан троуглу АБЦ, са врхом Ф који одговара темену Ц, мера $угла ∠ {Ф}$ једнака је мери $угла ∠ {Ц}$. Дакле, $син Ф = син Ц$. Од дужина страница троугла АБЦ,
$$синФ ={супротно сиде}/{хипотенусе}={АБ}/{АЦ}={12}/{20}={3}/{5}$$
Дакле, $синФ ={3}/{5}$.
Коначни одговор је ${3}/{5}$ или 0,6.
Питања из математике за САТ дозвољена за калкулатор
Питање 7

Непотпуна табела изнад сумира број ученика леворуких и десноруких ученика према полу за ученике осмог разреда средње школе Кеисел. Десноруких ученица има 5 пута више него леворуких, а 9 пута више дешњака него леворуких ученика. ако у школи има укупно 18 леворуких ученика и 122 дешњака, шта је од следећег најближе вероватноћи да је случајно одабран дешњак женског пола? (Напомена: Претпоставимо да ниједан ученик осмог разреда није и дешњак и леворук.)
А) 0,410
Б) 0,357
Ц) 0,333
Д) 0,250
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте решили овај проблем, требало би да направите две једначине користећи две променљиве ($к$ и $и$) и информације које сте добили. Нека је $к$ број леворуких ученица и нека је $и$ број леворуких ученика. Користећи информације дате у задатку, број дешњака ће бити $5к$, а број дешњака ће бити $9и$. Пошто је укупан број леворуких ученика 18, а укупан број дешњака 122, систем једначина испод мора да буде тачан:
$$к + и = 18$$
$$5к + 9и = 122$$
Када решите овај систем једначина, добијате $к = 10$ и $и = 8$. Дакле, 5*10, односно 50, од 122 дешњака су жене. Према томе, вероватноћа да је дешњак изабран насумично женско је ${50}/{122}$, што је на најближи хиљадити део 0,410.
Коначан одговор је А.Питања 8 и 9
Користите следеће информације и за питање 7 и за питање 8.
Ако купци уђу у продавницу просечном брзином од $р$ купаца по минуту и сваки остане у продавници просечно време од $Т$ минута, даје се просечан број купаца у продавници, $Н$, у било ком тренутку по формули $Н=рТ$. Овај однос је познат као Литлов закон.
Власник Гоод Деалс Сторе-а процењује да током радног времена у продавницу уђу у просеку 3 купца у минуту и да се сваки од њих задржава у просеку 15 минута. Власник продавнице користи Литлов закон да процени да у продавници у сваком тренутку има 45 купаца.
Питање 8
Литтлеов закон се може применити на било који део продавнице, као што је одређено одељење или редови на благајни. Власник продавнице утврђује да током радног времена отприлике 84 купца по сату обави куповину и сваки од ових купаца проведе у просеку 5 минута на каси. У било ком тренутку током радног времена, колико отприлике купаца у просеку чека у реду за касу да обави куповину у продавници Гоод Деалс?
ОБЈАШЊЕЊЕ ОДГОВОРА: Пошто питање каже да се Литлов закон може применити на било који део продавнице (на пример, само на ред за одјаву), онда је просечан број купаца, $Н$, у реду за одјаву у било ком тренутку $Н = рТ $, где је $р$ број купаца који улазе у ред за одјаву по минуту, а $Т$ је просечан број минута које сваки купац проведе у реду за плаћање.
Пошто 84 купца на сат обави куповину, 84 купца по сату улази у ред за одјаву. Међутим, ово треба да се конвертује у број купаца у минути (да би се користило са $Т = 5$). Пошто у једном сату има 60 минута, цена је {84 $ купаца по сату}/{60 минута} = 1,4$ купаца по минуту. Коришћење дате формуле са $р = 1.4$ и $Т = 5$ даје принос
$$Н = рт = (1.4)(5) = 7$$
Према томе, просечан број купаца, $Н$, у реду за касу у било ком тренутку током радног времена је 7.
Коначан одговор је 7.
Питање 9
Власник продавнице Гоод Деалс отвара нову продавницу широм града. За нову радњу, власник процењује да ће током радног времена у просеку бити око 90 купаца посатуђу у продавницу и сваки од њих остаје у просеку 12 минута. Просечан број купаца у новој продавници у било ком тренутку је који проценат мањи од просечног броја купаца у оригиналној продавници у било ком тренутку? (Напомена: Занемарите симбол за проценат када уносите свој одговор. На пример, ако је одговор 42,1%, унесите 42,1)
ОБЈАШЊЕЊЕ ОДГОВОРА: Према првобитним информацијама, процењени просечан број купаца у првобитној продавници у било ком тренутку (Н) је 45. У питању се наводи да у новој продавници менаџер процењује да је просечно 90 купаца на сат (60 минута) уђите у продавницу, што је еквивалентно 1,5 купаца у минути (р). Менаџер такође процењује да сваки купац остаје у продавници у просеку 12 минута (Т). Дакле, према Литловом закону, у новој продавници у било ком тренутку има, у просеку, $Н = рТ = (1,5)(12) = 18$ купаца. Ово је
$${45-18}/{45} * 100 = 60$$
проценат мање од просечног броја купаца у оригиналној продавници у било ком тренутку.
Коначан одговор је 60.
Питање 10
У $ки$-равни, тачка $(п,р)$ лежи на правој са једначином $и=к+б$, где је $б$ константа. Тачка са координатама $(2п, 5р)$ лежи на правој са једначином $и=2к+б$. Ако је $п=0$, колика је вредност $р/п$?
А) $2/5$
Б) $3/4$
Ц) $4/3$
Д) $5/2$
ОБЈАШЊЕЊЕ ОДГОВОРА: Пошто тачка $(п,р)$ лежи на правој са једначином $и=к+б$, та тачка мора да задовољи једначину. Замена $п$ за $к$ и $р$ за $и$ у једначини $и=к+б$ даје $р=п+б$, или $би б$ = $би р-би п $.
Слично томе, пошто тачка $(2п,5р)$ лежи на правој са једначином $и=2к+б$, тачка мора да задовољава једначину. Замена $2п$ за $к$ и $5р$ за $и$ у једначини $и=2к+б$ даје:
$5р=2(2п)+б$
$5р=4п+б$
$би б$ = $бо 5 би р-бо 4би п$.
Затим, можемо поставити две једначине једнаке $б$ једна другој и поједноставити:
$б=р-п=5р-4п$
$3п=4р$
Коначно, да бисмо пронашли $р/п$, морамо да поделимо обе стране једначине са $п$ и са $4$:
$3п=4р$
$3={4р}/п$
$3/4=р/п$
Тачан одговор је Б , $3/4$.
Ако сте изабрали изборе А и Д, можда сте погрешно формирали свој одговор од коефицијената у тачки $(2п, 5р)$. Ако сте изабрали избор Ц, можда сте побркали $р$ и $п$.
Имајте на уму да док се ово налази у одељку за калкулатор САТ-а, апсолутно вам није потребан ваш калкулатор да бисте га решили!
Питање 11
 Силос за жито је изграђен од два десна кружна конуса и десног кружног цилиндра са унутрашњим мерама приказаним на слици изнад. Од следећег, који је најближи запремини силоса за зрно, у кубним стопама?
Силос за жито је изграђен од два десна кружна конуса и десног кружног цилиндра са унутрашњим мерама приказаним на слици изнад. Од следећег, који је најближи запремини силоса за зрно, у кубним стопама?
А) 261,8
Б) 785,4
Ц) 916.3
Д) 1047.2
ОБЈАШЊЕЊЕ ОДГОВОРА: Запремина силоса за зрно може се наћи додавањем запремина свих чврстих материја од којих се састоји (цилиндра и два конуса). Силос се састоји од цилиндра (висине 10 стопа и полупречника основе 5 стопа) и два конуса (сваки са висином 5 стопа и полупречником основе 5 стопа). Формуле дате на почетку одељка САТ математике:
Запремина конуса
$$В={1}/{3}πр^2х$$
Запремина цилиндра
$$В=πр^2х$$
може се користити за одређивање укупне запремине силоса. Пошто два конуса имају идентичне димензије, укупна запремина силоса, у кубним стопама, дата је као
$$В_{сило}=π(5^2)(10)+(2)({1}/{3})π(5^2)(5)=({4}/{3})(250 )п$$
што је приближно једнако 1.047,2 кубних стопа.
Коначан одговор је Д.
Питање 12
Ако је $к$ просек (аритметичка средина) од $м$ и $9$, $и$ је просек од $2м$ и $15$, а $з$ је просек од $3м$ и $18$, шта је просек од $к$, $и$ и $з$ у смислу $м$?
А) $м+6$
Б) $м+7$
Ц) 2 милиона долара + 14 долара
Д) 3 милиона долара + 21 долара
ОБЈАШЊЕЊЕ ОДГОВОРА: Пошто је просек (аритметичка средина) два броја једнак збиру два броја подељен са 2, једначине $к={м+9}/{2}$, $и={2м+15}/{2 }$, $з={3м+18}/{2}$ су тачне. Просек за $к$, $и$ и $з$ је дат са ${к + и + з}/{3}$. Замена израза у м за сваку променљиву ($к$, $и$, $з$) даје
$$[{м+9}/{2}+{2м+15}/{2}+{3м+18}/{2}]/3$$
Овај разломак се може поједноставити на $м + 7$.
Коначни одговор је Б.
Питање 13
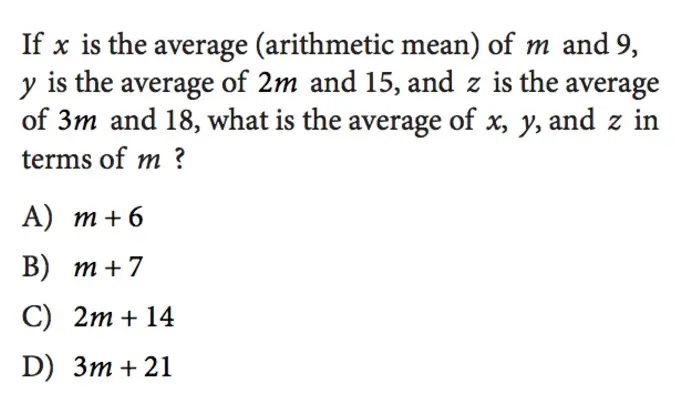
Функција $ф(к)=к^3-к^2-к-{11/4}$ је графички приказана у горњој $ки$-равни. Ако је $к$ константа таква да једначина $ф(к)=к$ има три реална решења, које од следећег може бити вредност $к$?
ОБЈАШЊЕЊЕ ОДГОВОРА: Једначина $ф(к) = к$ даје решења система једначина
$$и = ф(к) = к^3-к^2-к-{11}/{4}$$
и
$$и = к$$
Реално решење система две једначине одговара тачки пресека графика двеју једначина у $ки$-равни.
График $и = к$ је хоризонтална линија која садржи тачку $(0, к)$ и три пута сече график кубичне једначине (пошто има три реална решења). С обзиром на график, једина хоризонтална линија која би три пута пресекла кубну једначину је линија са једначином $и = −3$, или $ф(к) = −3$. Дакле, $к$ је $-3$.
Коначан одговор је Д.
Питање 14
$$к={1/2}нв^2$$
Динамички притисак $к$ генерисан флуидом који се креће брзином $в$ може се наћи коришћењем формуле изнад, где је $н$ константна густина течности. Аеронаутички инжењер користи формулу да пронађе динамички притисак флуида који се креће брзином $в$ и исте течности која се креће брзином 1,5$в$. Колики је однос динамичког притиска бржег флуида и динамичког притиска спорије течности?
ОБЈАШЊЕЊЕ ОДГОВОРА: Да бисте решили овај проблем, потребно је да поставите једначине са променљивим. Нека је $к_1$ динамички притисак спорије течности која се креће брзином $в_1$, а нека је $к_2$ динамички притисак брже течности која се креће брзином $в_2$. Онда
$$в_2 =1,5в_1$$
Узимајући у обзир једначину $к = {1}/{2}нв^2$, замена динамичког притиска и брзине бржег флуида даје $к_2 = {1}/{2}н(в_2)^2$. Пошто је $в_2 =1.5в_1$, израз $1.5в_1$ може бити замењен са $в_2$ у овој једначини, дајући $к_2 = {1}/{2}н(1.5в_1)^2$. Узимајући на квадрат $1,5$, можете преписати претходну једначину као
$$к_2 = (2.25)({1}/{2})н(в_1)^2 = (2.25)к_1$$
Дакле, однос динамичког притиска бржег флуида је
$${к2}/{к1} = {2,25 к_1}/{к_1}= 2,25 $$
Коначан одговор је 2,25 или 9/4.
Питање 15
За полином $п(к)$, вредност $п(3)$ је $-2$. Шта од следећег мора бити тачно за $п(к)$?
А) $к-5$ је фактор од $п(к)$.
Б) $к-2$ је фактор од $п(к)$.
Ц) $к+2$ је фактор од $п(к)$.
Д) Остатак када се $п(к)$ подели са $к-3$ је $-2$.
ОБЈАШЊЕЊЕ ОДГОВОРА: Ако је полином $п(к)$ подељен полиномом облика $к+к$ (који обухвата све могуће изборе одговора у овом питању), резултат се може написати као
$${п(к)}/{к+к}=к(к)+{р}/{к+к}$$
где је $к(к)$ полином, а $р$ остатак. Пошто је $к + к$ полином степена 1 (што значи да укључује само $к^1$ и нема виших експонента), остатак је реалан број.
Према томе, $п(к)$ се може преписати као $п(к) = (к + к)к(к) + р$, где је $р$ реалан број.
Питање гласи да је $п(3) = -2$, тако да мора бити тачно да
$$-2 = п(3) = (3 + к)к(3) + р$$
Сада можемо укључити све могуће одговоре. Ако је одговор А, Б или Ц, $р$ ће бити $0$, док ако је одговор Д, $р$ ће бити $-2$.
А. $-2 = п(3) = (3 + (-5))к(3) + 0$
$-2=(3-5)к(3)$
$-2=(-2)к(3)$
Ово би могло бити тачно, али само ако је $к(3)=1$
Б. $-2 = п(3) = (3 + (-2))к(3) + 0$
$-2 = (3-2)к(3)$
$-2 = (-1)к(3)$
Ово би могло бити тачно, али само ако је $к(3)=2$
Ц. $-2 = п(3) = (3 + 2)к(3) + 0$
$-2 = (5)к(3)$
Ово би могло бити тачно, али само ако је $к(3)={-2}/{5}$
Д. $-2 = п(3) = (3 + (-3))к(3) + (-2)$
$-2 = (3 - 3)к(3) + (-2)$
$-2 = (0)к(3) + (-2)$
Ово ће увек буди истинит без обзира шта је $к(3)$.
Од избора одговора, једини који мора ако је тачно да је $п(к)$ Д, да је остатак када се $п(к)$ подели са $к-3$ -2.
Коначан одговор је Д.

Заслужујеш све дремке након што прођеш кроз та питања.
Шта је заједничко најтежим САТ математичким питањима?
Важно је разумети шта ова тешка питања чини „тешким“. На тај начин ћете моћи да разумете и решите слична питања када их видите на дан тестирања, као и да имате бољу стратегију за идентификацију и исправљање ваших претходних САТ математичких грешака.
У овом одељку ћемо погледати шта ова питања имају заједничко и дати примере сваке врсте. Неки од разлога зашто су најтежа математичка питања најтежа математичка питања су:
#1: Тестирајте неколико математичких концепата одједном

Овде морамо да се бавимо замишљеним бројевима и разломцима одједном.
Тајна успеха: Размислите коју применљиву математику можете користити да решите проблем, радите корак по корак и испробајте сваку технику док не пронађете ону која функционише!
#2: Укључује много корака
Запамтите: што више корака треба да предузмете, лакше ћете забрљати негде на линији!
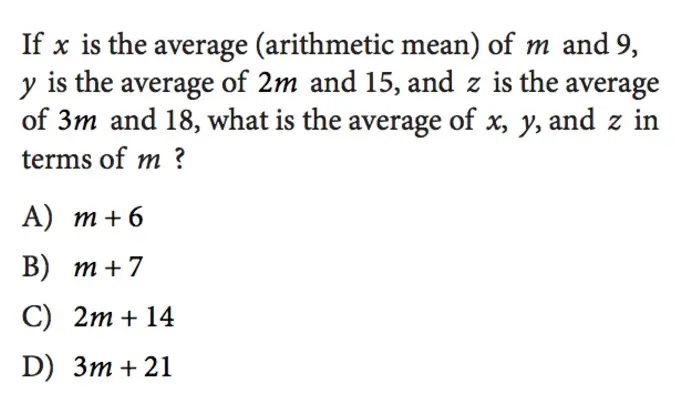
Морамо да решимо овај проблем у корацима (радећи неколико просека) да бисмо откључали остатак одговора у домино ефекту. Ово може бити збуњујуће, посебно ако сте под стресом или вам понестаје времена.
Тајна успеха: Полако, идите корак по корак и још једном проверите свој рад како не бисте погрешили!
#3: Тестирајте концепте са којима сте ограничено упознати
На пример, многи ученици су мање упознати са функцијама него са разломцима и процентима, тако да се већина функционалних питања сматра проблемима „високе тежине“.

Ако не знате како се сналазите у функцијама, ово би био тежак проблем.
Тајна успеха: Прегледајте математичке концепте са којима нисте толико упознати, као што су функције. Предлажемо да користите наше сјајне бесплатне САТ Матх водиче за преглед.
#4: Написане су на необичне или замршене начине
Може бити тешко схватити која су тачно нека питања питајући , а још мање схватити како их решити. Ово је посебно тачно када се питање налази на крају одељка, а понестаје вам времена.

Пошто ово питање пружа толико информација без дијаграма, може бити тешко загонетнути у ограниченом дозвољеном времену.
Тајна успеха: Узмите си времена, анализирајте шта се од вас тражи и нацртајте дијаграм ако вам је од помоћи.
#5: Користите много различитих варијабли

Са толико различитих варијабли у игри, прилично је лако доћи до забуне.
Тајна успеха: Узмите си времена, анализирајте шта се од вас тражи и размислите да ли је додавање бројева добра стратегија за решавање проблема (то не би било за горње питање, али би било за многа друга питања о променљивој САТ).
Тхе Таке-Аваис
САТ је маратон и што сте боље припремљени за њега, боље ћете се осећати на дан тестирања. Ако знате како да се носите са најтежим питањима која вам тест може поставити, чиниће полагање правог САТ-а много мање застрашујућим.
Ако сте сматрали да су ова питања лака, пазите да не потцењујете ефекат адреналина и умора на вашу способност решавања проблема. Док настављате да учите, увек се придржавајте одговарајућих смерница за време и покушајте да урадите пуне тестове кад год је то могуће. Ово је најбољи начин да поново креирате стварно окружење за тестирање како бисте се могли припремити за прави посао.
Ако сматрате да су ова питања изазовна, обавезно ојачајте своје знање математике тако што ћете погледати наше индивидуалне математичке водиче за САТ. Тамо ћете видети детаљнија објашњења тема о којима је реч, као и детаљније рашчлањивање одговора.
Шта је следеће?
Осетили сте да су ова питања тежа него што сте очекивали? Погледајте све теме обухваћене у САТ одељку из математике, а затим забележите који одељци су вам представљали посебну потешкоћу. Затим погледајте наше индивидуалне математичке водиче који ће вам помоћи да учврстите било коју од тих слабих области.
Понестаје вам времена за САТ математичку секцију? Наш водич ће вам помоћи да победите сат и повећате свој резултат.
Циљате на савршен резултат? Провери наш водич о томе како да добијете савршених 800 на САТ одељку из математике , који је написао савршени стрелац.
$, док ако је одговор Д, $р$ ће бити $-2$.
А. $-2 = п(3) = (3 + (-5))к(3) + 0$
$-2=(3-5)к(3)$
$-2=(-2)к(3)$
Ово би могло бити тачно, али само ако је $к(3)=1$
Б. $-2 = п(3) = (3 + (-2))к(3) + 0$
$-2 = (3-2)к(3)$
$-2 = (-1)к(3)$
Ово би могло бити тачно, али само ако је $к(3)=2$
Ц. $-2 = п(3) = (3 + 2)к(3) + 0$
$-2 = (5)к(3)$
Ово би могло бити тачно, али само ако је $к(3)={-2}/{5}$
Д. $-2 = п(3) = (3 + (-3))к(3) + (-2)$
$-2 = (3 - 3)к(3) + (-2)$
$-2 = (0)к(3) + (-2)$
Ово ће увек буди истинит без обзира шта је $к(3)$.
Од избора одговора, једини који мора ако је тачно да је $п(к)$ Д, да је остатак када се $п(к)$ подели са $к-3$ -2.
Коначан одговор је Д.

Заслужујеш све дремке након што прођеш кроз та питања.
Шта је заједничко најтежим САТ математичким питањима?
Важно је разумети шта ова тешка питања чини „тешким“. На тај начин ћете моћи да разумете и решите слична питања када их видите на дан тестирања, као и да имате бољу стратегију за идентификацију и исправљање ваших претходних САТ математичких грешака.
У овом одељку ћемо погледати шта ова питања имају заједничко и дати примере сваке врсте. Неки од разлога зашто су најтежа математичка питања најтежа математичка питања су:
#1: Тестирајте неколико математичких концепата одједном

Овде морамо да се бавимо замишљеним бројевима и разломцима одједном.
Тајна успеха: Размислите коју применљиву математику можете користити да решите проблем, радите корак по корак и испробајте сваку технику док не пронађете ону која функционише!
#2: Укључује много корака
Запамтите: што више корака треба да предузмете, лакше ћете забрљати негде на линији!
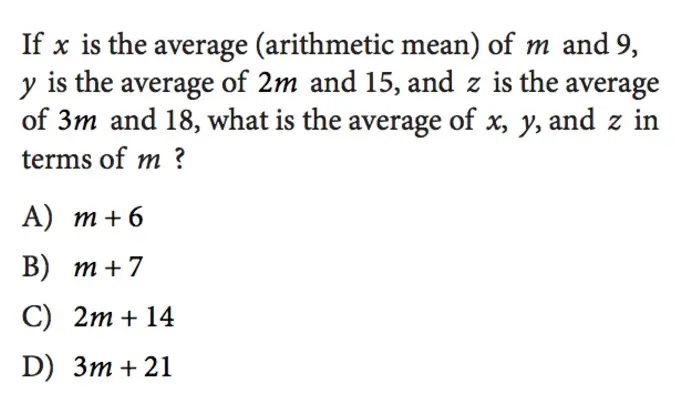
Морамо да решимо овај проблем у корацима (радећи неколико просека) да бисмо откључали остатак одговора у домино ефекту. Ово може бити збуњујуће, посебно ако сте под стресом или вам понестаје времена.
Тајна успеха: Полако, идите корак по корак и још једном проверите свој рад како не бисте погрешили!
#3: Тестирајте концепте са којима сте ограничено упознати
На пример, многи ученици су мање упознати са функцијама него са разломцима и процентима, тако да се већина функционалних питања сматра проблемима „високе тежине“.

Ако не знате како се сналазите у функцијама, ово би био тежак проблем.
Тајна успеха: Прегледајте математичке концепте са којима нисте толико упознати, као што су функције. Предлажемо да користите наше сјајне бесплатне САТ Матх водиче за преглед.
#4: Написане су на необичне или замршене начине
Може бити тешко схватити која су тачно нека питања питајући , а још мање схватити како их решити. Ово је посебно тачно када се питање налази на крају одељка, а понестаје вам времена.

Пошто ово питање пружа толико информација без дијаграма, може бити тешко загонетнути у ограниченом дозвољеном времену.
Тајна успеха: Узмите си времена, анализирајте шта се од вас тражи и нацртајте дијаграм ако вам је од помоћи.
#5: Користите много различитих варијабли

Са толико различитих варијабли у игри, прилично је лако доћи до забуне.
Тајна успеха: Узмите си времена, анализирајте шта се од вас тражи и размислите да ли је додавање бројева добра стратегија за решавање проблема (то не би било за горње питање, али би било за многа друга питања о променљивој САТ).
Тхе Таке-Аваис
САТ је маратон и што сте боље припремљени за њега, боље ћете се осећати на дан тестирања. Ако знате како да се носите са најтежим питањима која вам тест може поставити, чиниће полагање правог САТ-а много мање застрашујућим.
Ако сте сматрали да су ова питања лака, пазите да не потцењујете ефекат адреналина и умора на вашу способност решавања проблема. Док настављате да учите, увек се придржавајте одговарајућих смерница за време и покушајте да урадите пуне тестове кад год је то могуће. Ово је најбољи начин да поново креирате стварно окружење за тестирање како бисте се могли припремити за прави посао.
линук фајл за промену
Ако сматрате да су ова питања изазовна, обавезно ојачајте своје знање математике тако што ћете погледати наше индивидуалне математичке водиче за САТ. Тамо ћете видети детаљнија објашњења тема о којима је реч, као и детаљније рашчлањивање одговора.
Шта је следеће?
Осетили сте да су ова питања тежа него што сте очекивали? Погледајте све теме обухваћене у САТ одељку из математике, а затим забележите који одељци су вам представљали посебну потешкоћу. Затим погледајте наше индивидуалне математичке водиче који ће вам помоћи да учврстите било коју од тих слабих области.
Понестаје вам времена за САТ математичку секцију? Наш водич ће вам помоћи да победите сат и повећате свој резултат.
Циљате на савршен резултат? Провери наш водич о томе како да добијете савршених 800 на САТ одељку из математике , који је написао савршени стрелац.





 Силос за жито је изграђен од два десна кружна конуса и десног кружног цилиндра са унутрашњим мерама приказаним на слици изнад. Од следећег, који је најближи запремини силоса за зрно, у кубним стопама?
Силос за жито је изграђен од два десна кружна конуса и десног кружног цилиндра са унутрашњим мерама приказаним на слици изнад. Од следећег, који је најближи запремини силоса за зрно, у кубним стопама?