Линеарна регресија и логистичка регресија су два позната алгоритма машинског учења који су под надзором технике учења. Пошто су оба алгоритма по природи надгледана, ови алгоритми користе означени скуп података да би направили предвиђања. Али главна разлика између њих је начин на који се користе. Линеарна регресија се користи за решавање проблема регресије, док се логистичка регресија користи за решавање проблема класификације. Опис оба алгоритма је дат у наставку заједно са табелом разлика.
Линеарна регресија:
- Линеарна регресија је један од најједноставнијих алгоритама машинског учења који спада у технику надгледаног учења и користи се за решавање проблема регресије.
- Користи се за предвиђање континуиране зависне променљиве уз помоћ независних променљивих.
- Циљ линеарне регресије је да пронађе најбољу линију која може тачно предвидети излаз за континуирану зависну променљиву.
- Ако се за предвиђање користи једна независна променљива, онда се то назива једноставна линеарна регресија, а ако постоји више од две независне променљиве онда се таква регресија назива вишеструка линеарна регресија.
- Проналажењем линије која најбоље одговара, алгоритам успоставља везу између зависне променљиве и независне променљиве. И однос треба да буде линеарне природе.
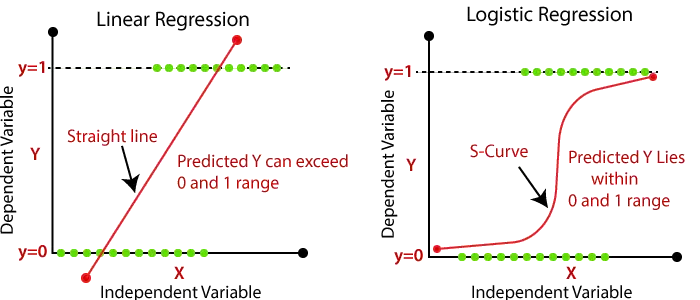
- Излаз за линеарну регресију треба да буду само континуиране вредности као што су цена, старост, плата, итд. Однос између зависне варијабле и независне варијабле може се приказати на слици испод:

На горњој слици зависна варијабла је на И-оси (плата), а независна варијабла на к-оси (искуство). Регресиона линија се може написати као:
y= a<sub>0</sub>+a<sub>1</sub>x+ ε
Где0и а1су коефицијенти и ε је члан грешке.
Логистичка регресија:
- Логистичка регресија је један од најпопуларнијих алгоритама машинског учења који спада у технике надгледаног учења.
- Може се користити за класификацију као и за проблеме регресије, али се углавном користи за проблеме класификације.
- Логистичка регресија се користи за предвиђање категоријалне зависне варијабле уз помоћ независних варијабли.
- Излаз проблема логистичке регресије може бити само између 0 и 1.
- Логистичка регресија се може користити тамо где се захтевају вероватноће између две класе. На пример, да ли ће падати киша данас или не, или 0 или 1, тачно или нетачно итд.
- Логистичка регресија се заснива на концепту процене максималне вероватноће. Према овој процени, посматрани подаци би требало да буду највероватнији.
- У логистичкој регресији, преносимо пондерисани збир улазних података кроз активациону функцију која може мапирати вредности између 0 и 1. Таква активациона функција је позната као сигмоидна функција а добијена крива се назива сигмоидна крива или С-крива. Размотрите слику испод:

- Једначина за логистичку регресију је:

Разлика између линеарне регресије и логистичке регресије:
| Линеарна регресија | Логистичка регресија |
|---|---|
| Линеарна регресија се користи за предвиђање континуиране зависне променљиве коришћењем датог скупа независних променљивих. | Логистичка регресија се користи за предвиђање категоријалне зависне променљиве коришћењем датог скупа независних варијабли. |
| Линеарна регресија се користи за решавање проблема регресије. | Логистичка регресија се користи за решавање класификационих проблема. |
| У линеарној регресији предвиђамо вредност континуираних променљивих. | У логистичкој регресији предвиђамо вредности категоричких варијабли. |
| У линеарној регресији налазимо линију која најбоље одговара, помоћу које можемо лако предвидети излаз. | У логистичкој регресији налазимо С-криву по којој можемо класификовати узорке. |
| Метода најмањег квадрата се користи за процену тачности. | За процену тачности користи се метод процене максималне вероватноће. |
| Излаз за линеарну регресију мора бити континуирана вредност, као што су цена, старост итд. | Излаз логистичке регресије мора бити категоричка вредност као што је 0 или 1, Да или Не, итд. |
| У линеарној регресији, захтева се да однос између зависне променљиве и независне променљиве мора бити линеаран. | У логистичкој регресији, није потребно имати линеарну везу између зависне и независне променљиве. |
| У линеарној регресији може постојати колинеарност између независних варијабли. | У логистичкој регресији не би требало да постоји колинеарност између независне променљиве. |
