Видели смо различите методе са различитим временским сложеностима за израчунавање ЛЦА у н-арном стаблу: -
Метод 1: Наивни метод (израчунавањем путање корена до чвора) | О(н) по упиту
Метод 2: Коришћење Скрт декомпозиције | О (скрт Х)
Метод 3: Коришћење приступа Спарсе Матрик ДП | О(пријава)
Хајде да проучимо другу методу која има брже време упита од свих горе наведених метода. Дакле, наш циљ ће бити да израчунамо ЛЦА у константно време ~ О(1) . Хајде да видимо како то можемо постићи.
Метод 4: Коришћење упита минималног опсега
Расправљали смо ЛЦА и РМК за бинарно стабло . Овде расправљамо о конверзији ЛЦА проблема у РМК за н-арно стабло.
Pre-requisites:- LCA in Binary Tree using RMQ RMQ using sparse table
Кључни концепт: У овој методи ћемо свести наш ЛЦА проблем на РМК (Ранге Минимум Куери) проблем преко статичког низа. Када то урадимо, онда ћемо повезати упите минималног опсега са потребним ЛЦА упитима.
Први корак ће бити декомпоновање стабла у раван линеарни низ. Да бисмо то урадили, можемо применити Ојлеров ход. Ојлерова шетња ће омогућити обилазак графа у претпродаји. Тако ћемо извршити Ојлерову шетњу на дрвету и ускладиштити чворове у низу док их посећујемо. Овај процес смањује дрво > 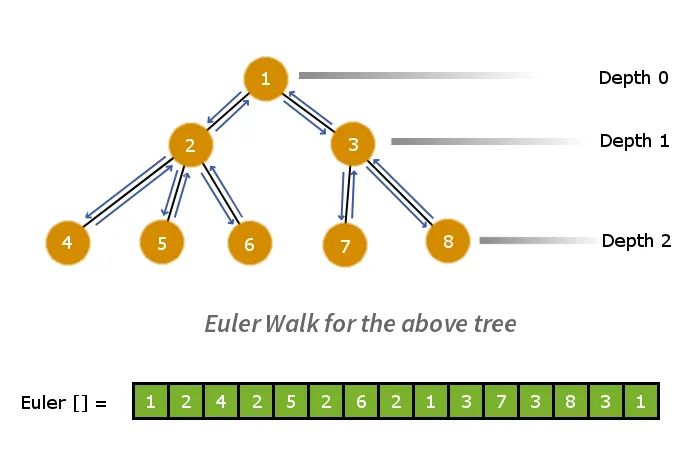
Хајде сада да размислимо општим речима: Размотримо било која два чвора на стаблу. Постојаће тачно једна путања која повезује оба чвора и чвор који има најмању вредност дубине у путањи биће ЛЦА два дата чвора.
Сада узмите било која два различита чвора рецимо ин и в у низу Ојлеровог хода. Сада ће сви елементи на путањи од у до в лежати између индекса чворова у и в у Ојлеровом низу хода. Зато само треба да израчунамо чвор са минималном дубином између индекса чвора у и чвора в у Ојлеровом низу.
За ово ћемо одржавати још један низ који ће садржати дубину свих чворова који одговарају њиховој позицији у Ојлеровом низу хода, тако да можемо да применимо наш РМК алгоритам на њега.
Доле је дат низ Ојлеровог хода паралелно са његовим низом трагова дубине.

јавасцрипт оператори
Пример: - Размотрите два чвора чвор 6 и чвор 7 у Ојлеровом низу. Да бисмо израчунали ЛЦА чвора 6 и чвора 7, тражимо најмању вредност дубине за све чворове између чвора 6 и чвора 7.
Стога чвор 1 има најмању вредност дубине = 0 и стога је то ЛЦА за чвор 6 и чвор 7.

Имплементација:-
We will be maintaining three arrays 1) Euler Path 2) Depth array 3) First Appearance Index
Низ Ојлерове путање и дубине су исти као што је горе описано
Индекс првог појављивања ФАИ[] : Низ индекса првог изгледа ће ускладиштити индекс за прву позицију сваког чвора у низу Ојлерове путање. ФАИ[и] = Прво појављивање и-тог чвора у Еулер Валк низу.
Имплементација горње методе је дата у наставку: -
Имплементација:
C++// C++ program to demonstrate LCA of n-ary tree // in constant time. #include 'bits/stdc++.h' using namespace std; #define sz 101 vector < int > adj[sz]; // stores the tree vector < int > euler; // tracks the eulerwalk vector < int > depthArr; // depth for each node corresponding // to eulerwalk int FAI[sz]; // stores first appearance index of every node int level[sz]; // stores depth for all nodes in the tree int ptr; // pointer to euler walk int dp[sz][18]; // sparse table int logn[sz]; // stores log values int p2[20]; // stores power of 2 void buildSparseTable(int n) { // initializing sparse table memset(dp-1sizeof(dp)); // filling base case values for (int i=1; i<n; i++) dp[i-1][0] = (depthArr[i]>depthArr[i-1])?i-1:i; // dp to fill sparse table for (int l=1; l<15; l++) for (int i=0; i<n; i++) if (dp[i][l-1]!=-1 and dp[i+p2[l-1]][l-1]!=-1) dp[i][l] = (depthArr[dp[i][l-1]]>depthArr[dp[i+p2[l-1]][l-1]])? dp[i+p2[l-1]][l-1] : dp[i][l-1]; else break; } int query(int lint r) { int d = r-l; int dx = logn[d]; if (l==r) return l; if (depthArr[dp[l][dx]] > depthArr[dp[r-p2[dx]][dx]]) return dp[r-p2[dx]][dx]; else return dp[l][dx]; } void preprocess() { // memorizing powers of 2 p2[0] = 1; for (int i=1; i<18; i++) p2[i] = p2[i-1]*2; // memorizing all log(n) values int val = 1ptr=0; for (int i=1; i<sz; i++) { logn[i] = ptr-1; if (val==i) { val*=2; logn[i] = ptr; ptr++; } } } /** * Euler Walk ( preorder traversal) * converting tree to linear depthArray * Time Complexity : O(n) * */ void dfs(int curint prevint dep) { // marking FAI for cur node if (FAI[cur]==-1) FAI[cur] = ptr; level[cur] = dep; // pushing root to euler walk euler.push_back(cur); // incrementing euler walk pointer ptr++; for (auto x:adj[cur]) { if (x != prev) { dfs(xcurdep+1); // pushing cur again in backtrack // of euler walk euler.push_back(cur); // increment euler walk pointer ptr++; } } } // Create Level depthArray corresponding // to the Euler walk Array void makeArr() { for (auto x : euler) depthArr.push_back(level[x]); } int LCA(int uint v) { // trivial case if (u==v) return u; if (FAI[u] > FAI[v]) swap(uv); // doing RMQ in the required range return euler[query(FAI[u] FAI[v])]; } void addEdge(int uint v) { adj[u].push_back(v); adj[v].push_back(u); } int main(int argc char const *argv[]) { // constructing the described tree int numberOfNodes = 8; addEdge(12); addEdge(13); addEdge(24); addEdge(25); addEdge(26); addEdge(37); addEdge(38); // performing required precalculations preprocess(); // doing the Euler walk ptr = 0; memset(FAI-1sizeof(FAI)); dfs(100); // creating depthArray corresponding to euler[] makeArr(); // building sparse table buildSparseTable(depthArr.size()); cout << 'LCA(67) : ' << LCA(67) << 'n'; cout << 'LCA(64) : ' << LCA(64) << 'n'; return 0; }
// Java program to demonstrate LCA of n-ary // tree in constant time. import java.util.ArrayList; import java.util.Arrays; class GFG{ static int sz = 101; @SuppressWarnings('unchecked') // Stores the tree static ArrayList<Integer>[] adj = new ArrayList[sz]; // Tracks the eulerwalk static ArrayList<Integer> euler = new ArrayList<>(); // Depth for each node corresponding static ArrayList<Integer> depthArr = new ArrayList<>(); // to eulerwalk // Stores first appearance index of every node static int[] FAI = new int[sz]; // Stores depth for all nodes in the tree static int[] level = new int[sz]; // Pointer to euler walk static int ptr; // Sparse table static int[][] dp = new int[sz][18]; // Stores log values static int[] logn = new int[sz]; // Stores power of 2 static int[] p2 = new int[20]; static void buildSparseTable(int n) { // Initializing sparse table for(int i = 0; i < sz; i++) { for(int j = 0; j < 18; j++) { dp[i][j] = -1; } } // Filling base case values for(int i = 1; i < n; i++) dp[i - 1][0] = (depthArr.get(i) > depthArr.get(i - 1)) ? i - 1 : i; // dp to fill sparse table for(int l = 1; l < 15; l++) for(int i = 0; i < n; i++) if (dp[i][l - 1] != -1 && dp[i + p2[l - 1]][l - 1] != -1) dp[i][l] = (depthArr.get(dp[i][l - 1]) > depthArr.get( dp[i + p2[l - 1]][l - 1])) ? dp[i + p2[l - 1]][l - 1] : dp[i][l - 1]; else break; } static int query(int l int r) { int d = r - l; int dx = logn[d]; if (l == r) return l; if (depthArr.get(dp[l][dx]) > depthArr.get(dp[r - p2[dx]][dx])) return dp[r - p2[dx]][dx]; else return dp[l][dx]; } static void preprocess() { // Memorizing powers of 2 p2[0] = 1; for(int i = 1; i < 18; i++) p2[i] = p2[i - 1] * 2; // Memorizing all log(n) values int val = 1 ptr = 0; for(int i = 1; i < sz; i++) { logn[i] = ptr - 1; if (val == i) { val *= 2; logn[i] = ptr; ptr++; } } } // Euler Walk ( preorder traversal) converting // tree to linear depthArray // Time Complexity : O(n) static void dfs(int cur int prev int dep) { // Marking FAI for cur node if (FAI[cur] == -1) FAI[cur] = ptr; level[cur] = dep; // Pushing root to euler walk euler.add(cur); // Incrementing euler walk pointer ptr++; for(Integer x : adj[cur]) { if (x != prev) { dfs(x cur dep + 1); // Pushing cur again in backtrack // of euler walk euler.add(cur); // Increment euler walk pointer ptr++; } } } // Create Level depthArray corresponding // to the Euler walk Array static void makeArr() { for(Integer x : euler) depthArr.add(level[x]); } static int LCA(int u int v) { // Trivial case if (u == v) return u; if (FAI[u] > FAI[v]) { int temp = u; u = v; v = temp; } // Doing RMQ in the required range return euler.get(query(FAI[u] FAI[v])); } static void addEdge(int u int v) { adj[u].add(v); adj[v].add(u); } // Driver code public static void main(String[] args) { for(int i = 0; i < sz; i++) { adj[i] = new ArrayList<>(); } // Constructing the described tree int numberOfNodes = 8; addEdge(1 2); addEdge(1 3); addEdge(2 4); addEdge(2 5); addEdge(2 6); addEdge(3 7); addEdge(3 8); // Performing required precalculations preprocess(); // Doing the Euler walk ptr = 0; Arrays.fill(FAI -1); dfs(1 0 0); // Creating depthArray corresponding to euler[] makeArr(); // Building sparse table buildSparseTable(depthArr.size()); System.out.println('LCA(67) : ' + LCA(6 7)); System.out.println('LCA(64) : ' + LCA(6 4)); } } // This code is contributed by sanjeev2552
# Python program to demonstrate LCA of n-ary tree # in constant time. from typing import List # stores the tree adj = [[] for _ in range(101)] # tracks the eulerwalk euler = [] # depth for each node corresponding to eulerwalk depthArr = [] # stores first appearance index of every node FAI = [-1] * 101 # stores depth for all nodes in the tree level = [0] * 101 # pointer to euler walk ptr = 0 # sparse table dp = [[-1] * 18 for _ in range(101)] # stores log values logn = [0] * 101 # stores power of 2 p2 = [0] * 20 def buildSparseTable(n: int): # initializing sparse table for i in range(n): dp[i][0] = i-1 if depthArr[i] > depthArr[i-1] else i # dp to fill sparse table for l in range(1 15): for i in range(n): if dp[i][l-1] != -1 and dp[i+p2[l-1]][l-1] != -1: dp[i][l] = dp[i+p2[l-1]][l-1] if depthArr[dp[i][l-1] ] > depthArr[dp[i+p2[l-1]][l-1]] else dp[i][l-1] else: break def query(l: int r: int) -> int: d = r-l dx = logn[d] if l == r: return l if depthArr[dp[l][dx]] > depthArr[dp[r-p2[dx]][dx]]: return dp[r-p2[dx]][dx] else: return dp[l][dx] def preprocess(): global ptr # memorizing powers of 2 p2[0] = 1 for i in range(1 18): p2[i] = p2[i-1]*2 # memorizing all log(n) values val = 1 ptr = 0 for i in range(1 101): logn[i] = ptr-1 if val == i: val *= 2 logn[i] = ptr ptr += 1 def dfs(cur: int prev: int dep: int): global ptr # marking FAI for cur node if FAI[cur] == -1: FAI[cur] = ptr level[cur] = dep # pushing root to euler walk euler.append(cur) # incrementing euler walk pointer ptr += 1 for x in adj[cur]: if x != prev: dfs(x cur dep+1) # pushing cur again in backtrack # of euler walk euler.append(cur) # increment euler walk pointer ptr += 1 # Create Level depthArray corresponding # to the Euler walk Array def makeArr(): global depthArr for x in euler: depthArr.append(level[x]) def LCA(u: int v: int) -> int: # trivial case if u == v: return u if FAI[u] > FAI[v]: u v = v u # doing RMQ in the required range return euler[query(FAI[u] FAI[v])] def addEdge(u v): adj[u].append(v) adj[v].append(u) # constructing the described tree numberOfNodes = 8 addEdge(1 2) addEdge(1 3) addEdge(2 4) addEdge(2 5) addEdge(2 6) addEdge(3 7) addEdge(3 8) # performing required precalculations preprocess() # doing the Euler walk ptr = 0 FAI = [-1] * (numberOfNodes + 1) dfs(1 0 0) # creating depthArray corresponding to euler[] makeArr() # building sparse table buildSparseTable(len(depthArr)) print('LCA(67) : ' LCA(6 7)) print('LCA(64) : ' LCA(6 4))
// C# program to demonstrate LCA of n-ary // tree in constant time. using System; using System.Collections.Generic; public class GFG { static int sz = 101; // Stores the tree static List<int>[] adj = new List<int>[sz]; // Tracks the eulerwalk static List<int> euler = new List<int>(); // Depth for each node corresponding static List<int> depthArr = new List<int>(); // to eulerwalk // Stores first appearance index of every node static int[] FAI = new int[sz]; // Stores depth for all nodes in the tree static int[] level = new int[sz]; // Pointer to euler walk static int ptr; // Sparse table static int[] dp = new int[sz 18]; // Stores log values static int[] logn = new int[sz]; // Stores power of 2 static int[] p2 = new int[20]; static void buildSparseTable(int n) { // Initializing sparse table for(int i = 0; i < sz; i++) { for(int j = 0; j < 18; j++) { dp[ij] = -1; } } // Filling base case values for(int i = 1; i < n; i++) dp[i - 10] = (depthArr[i] > depthArr[i - 1]) ? i - 1 : i; // dp to fill sparse table for(int l = 1; l < 15; l++) for(int i = 0; i < n; i++) if (dp[il - 1] != -1 && dp[i + p2[l - 1]l - 1] != -1) dp[il] = (depthArr[dp[il - 1]] > depthArr[dp[i + p2[l - 1]l - 1]]) ? dp[i + p2[l - 1]l - 1] : dp[il - 1]; else break; } static int query(int l int r) { int d = r - l; int dx = logn[d]; if (l == r) return l; if (depthArr[dp[ldx]] > depthArr[dp[r - p2[dx]dx]]) return dp[r - p2[dx]dx]; else return dp[ldx]; } static void preprocess() { // Memorizing powers of 2 p2[0] = 1; for(int i = 1; i < 18; i++) p2[i] = p2[i - 1] * 2; // Memorizing all log(n) values int val = 1 ptr = 0; for(int i = 1; i < sz; i++) { logn[i] = ptr - 1; if (val == i) { val *= 2; logn[i] = ptr; ptr++; } } } // Euler Walk ( preorder traversal) converting // tree to linear depthArray // Time Complexity : O(n) static void dfs(int cur int prev int dep) { // Marking FAI for cur node if (FAI[cur] == -1) FAI[cur] = ptr; level[cur] = dep; // Pushing root to euler walk euler.Add(cur); // Incrementing euler walk pointer ptr++; foreach (int x in adj[cur]) { if (x != prev) { dfs(x cur dep + 1); euler.Add(cur); ptr++; } } } // Create Level depthArray corresponding // to the Euler walk Array static void makeArr() { foreach (int x in euler) depthArr.Add(level[x]); } static int LCA(int u int v) { // Trivial case if (u == v) return u; if (FAI[u] > FAI[v]) { int temp = u; u = v; v = temp; } // Doing RMQ in the required range return euler[query(FAI[u] FAI[v])]; } static void addEdge(int u int v) { adj[u].Add(v); adj[v].Add(u); } // Driver Code static void Main(string[] args) { int sz = 9; adj = new List<int>[sz]; for (int i = 0; i < sz; i++) { adj[i] = new List<int>(); } // Constructing the described tree int numberOfNodes = 8; addEdge(1 2); addEdge(1 3); addEdge(2 4); addEdge(2 5); addEdge(2 6); addEdge(3 7); addEdge(3 8); // Performing required precalculations preprocess(); // Doing the Euler walk ptr = 0; Array.Fill(FAI -1); dfs(1 0 0); // Creating depthArray corresponding to euler[] makeArr(); // Building sparse table buildSparseTable(depthArr.Count); Console.WriteLine('LCA(67) : ' + LCA(6 7)); Console.WriteLine('LCA(64) : ' + LCA(6 4)); } } // This code is contributed by Prince Kumar
let adj = []; for (let _ = 0; _ < 101; _++) { adj.push([]); } // tracks the eulerwalk let euler = []; // depth for each node corresponding to eulerwalk let depthArr = []; // stores first appearance index of every node let FAI = new Array(101).fill(-1); // stores depth for all nodes in the tree let level = new Array(101).fill(0); // pointer to euler walk let ptr = 0; // sparse table let dp = []; for (let _ = 0; _ < 101; _++) { dp.push(new Array(18).fill(-1)); } // stores log values let logn = new Array(101).fill(0); // stores power of 2 let p2 = new Array(20).fill(0); function buildSparseTable(n) { // initializing sparse table for (let i = 0; i < n; i++) { dp[i][0] = i - 1 >= 0 && depthArr[i] > depthArr[i - 1] ? i - 1 : i; } // dp to fill sparse table for (let l = 1; l < 15; l++) { for (let i = 0; i < n; i++) { if ( dp[i][l - 1] !== -1 && dp[i + p2[l - 1]][l - 1] !== -1 ) { dp[i][l] = depthArr[dp[i][l - 1]] > depthArr[dp[i + p2[l - 1]][l - 1]] ? dp[i + p2[l - 1]][l - 1] : dp[i][l - 1]; } else { break; } } } } function query(l r) { let d = r - l; let dx = logn[d]; if (l === r) { return l; } if (depthArr[dp[l][dx]] > depthArr[dp[r - p2[dx]][dx]]) { return dp[r - p2[dx]][dx]; } else { return dp[l][dx]; } } function preprocess() { // memorizing powers of 2 p2[0] = 1; for (let i = 1; i < 18; i++) { p2[i] = p2[i - 1] * 2; } // memorizing all log(n) values let val = 1; ptr = 0; for (let i = 1; i < 101; i++) { logn[i] = ptr - 1; if (val === i) { val *= 2; logn[i] = ptr; ptr += 1; } } } function dfs(cur prev dep) { // marking FAI for cur node if (FAI[cur] === -1) { FAI[cur] = ptr; } level[cur] = dep; // pushing root to euler walk euler.push(cur); // incrementing euler walk pointer ptr += 1; for (let x of adj[cur]) { if (x !== prev) { dfs(x cur dep + 1); // pushing cur again in backtrack // of euler walk euler.push(cur); // increment euler walk pointer ptr += 1; } } } // Create Level depthArray corresponding // to the Euler walk Array function makeArr() { for (let x of euler) { depthArr.push(level[x]); } } function LCA(u v) { // trivial case if (u === v) { return u; } if (FAI[u] > FAI[v]) { [u v] = [v u]; } // doing RMQ in the required range return euler[query(FAI[u] FAI[v])]; } function addEdge(u v) { adj[u].push(v); adj[v].push(u); } // constructing the described tree let numberOfNodes = 8; addEdge(1 2); addEdge(1 3); addEdge(2 4); addEdge(2 5); addEdge(2 6); addEdge(3 7); addEdge(3 8); // performing required precalculations preprocess(); // doing the Euler walk ptr = 0; FAI = new Array(numberOfNodes + 1).fill(-1); dfs(1 0 0); // creating depthArray corresponding to euler[] makeArr(); // building sparse table buildSparseTable(depthArr.length); console.log('LCA(67) : ' LCA(6 7)); console.log('LCA(64) : ' LCA(6 4));
Излаз
LCA(67) : 1 LCA(64) : 2
Напомена : Претходно израчунавамо сву потребну снагу 2 и такође унапред израчунавамо све потребне вредности дневника да бисмо обезбедили константну временску сложеност по упиту. У супротном, да смо израчунали дневник за сваку операцију упита, наша временска сложеност не би била константна.
Временска сложеност: Процес конверзије из ЛЦА у РМК обавља Еулер Валк који траје О(н) време.
Претходна обрада за ретку табелу у РМК траје О(нлогн) времена и одговарање на сваки упит је процес са константним временом. Према томе, укупна временска сложеност је О(нлогн) – претходна обрада и О(1) за сваки упит.
Помоћни простор: О(н+с)
латекс матрицаКреирај квиз
