• Алгоритам за пењање по брду је алгоритам локалног претраживања који се непрекидно креће у правцу повећања надморске висине/вредности да би пронашао врх планине или најбоље решење за проблем. Прекида се када достигне вршну вредност где ниједан сусед нема већу вредност.
• Алгоритам за пењање по брду је техника која се користи за оптимизацију математичких проблема. Један од широко расправљених примера алгоритма за пењање по брду је проблем Путујући продавац у коме морамо да минимизирамо раздаљину коју је прешао продавац.
• Назива се и похлепном локалном потрагом јер гледа само на своју добру непосредну суседну државу, а не даље од тога.
• Чвор алгоритма за пењање по брду има две компоненте које су стање и вредност.
• Пењање на брдо се углавном користи када је доступна добра хеуристика.
• У овом алгоритму, не морамо да одржавамо и рукујемо стаблом претраге или графом јер задржава само једно тренутно стање.

Карактеристике пењања на брдо:

Следе неке главне карактеристике алгоритма за пењање по брду:

Генериши и тестирај варијанту:Пењање на брдо је варијанта Генерате анд Тест методе. Метода Генерате анд Тест производи повратну информацију која помаже да се одлучи у ком правцу да се креће у простору за претрагу.Похлепан приступ:Претрага алгоритма за пењање се креће у правцу који оптимизује трошкове.Без враћања уназад:Не враћа простор за претрагу, јер не памти претходна стања.

Дијаграм простора и стања за пењање по брду:

Пејзаж простора стања је графички приказ алгоритма за пењање по брду који приказује график између различитих стања алгоритма и циљне функције/цена.

На И-оси смо узели функцију која може бити функција циља или функција трошкова, и простор стања на к-оси. Ако је функција на И оси коштана, онда је циљ претраге да се пронађе глобални минимум и локални минимум. Ако је функција И-осе функција циља, онда је циљ претраге да се пронађе глобални максимум и локални максимум.

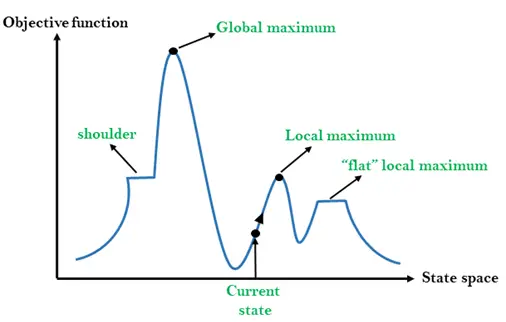
Различити региони у пејзажу државног простора:

Локални максимум: Локални максимум је држава која је боља од суседних држава, али постоји и друга држава која је виша од њега.

Глобални максимум: Глобални максимум је најбоље могуће стање пејзажа државног простора. Има највећу вредност функције циља.

Тренутно стање: То је стање у пејзажном дијаграму где је агент тренутно присутан.

Равни локални максимум: То је раван простор у пејзажу где све суседне државе тренутних држава имају исту вредност.

раме: То је висоравни регион који има ивицу узбрдо.

Врсте алгоритама за пењање по брду:

• Једноставно пењање на брдо:
• Најстрмији успон уз брдо:
• Стохастичко пењање на брдо:

1. Једноставно пењање на брдо:

Једноставно пењање на брдо је најједноставнији начин за имплементацију алгоритма за пењање. Он само процењује стање суседног чвора истовремено и бира први који оптимизује тренутну цену и поставља га као тренутно стање . Проверава само да је то једно стање наследника, и ако нађе боље од тренутног стања, онда премести друго да буде у истом стању. Овај алгоритам има следеће карактеристике:

• Мање одузима време
• Мање оптимално решење и решење није загарантовано

Алгоритам за једноставно пењање на брдо:

Корак 1:Процените почетно стање, ако је циљно стање онда вратите успех и Стоп.Корак 2:Петља Док се не пронађе решење или док не преостане ниједан нови оператор за примену.Корак 3:Изаберите и примените оператор на тренутно стање.4. корак:Проверите ново стање:
1. Ако је циљ стање, онда вратите успех и одустаните.
2. Иначе, ако је боље од тренутног стања, доделите ново стање као тренутно стање.
3. Иначе, ако не и боље од тренутног стања, вратите се на корак 2.
5. корак:Изађи.

2. Најстрмији успон уз брдо:

Алгоритам за најстрмији успон је варијација једноставног алгоритма за пењање. Овај алгоритам испитује све суседне чворове тренутног стања и бира један суседни чвор који је најближи циљном стању. Овај алгоритам троши више времена док тражи више суседа

Алгоритам за најстрмији успон уз брдо:

Корак 1:Процијените почетно стање, ако је циљно стање онда вратите успјех и зауставите се, у супротном учините тренутно стање као почетно стање.Корак 2:Петља док се не пронађе решење или се тренутно стање не промени.
1. Нека СУЦЦ буде држава таква да ће сваки наследник садашње државе бити бољи од ње.
2. За сваки оператор који се односи на тренутно стање:
   1. Примените нови оператор и генеришите ново стање.
   2. Оцените ново стање.
   3. Ако је циљно стање, вратите га и напустите, иначе га упоредите са СУЦЦ-ом.
   4. Ако је боље од СУЦЦ, онда поставите ново стање као СУЦЦ.
   5. Ако је СУЦЦ бољи од тренутног стања, подесите тренутно стање на СУЦЦ.
5. корак:Изађи.

3. Стохастичко пењање:

Стохастичко пењање на брдо не испитује све своје суседе пре кретања. Уместо тога, овај алгоритам претраге бира један суседни чвор насумично и одлучује да ли да га одабере као тренутно стање или да испита друго стање.

Проблеми у алгоритму за пењање по брду:

1. Локални максимум: Локални максимум је вршно стање у пејзажу које је боље од сваке од суседних држава, али постоји и друго стање које је веће од локалног максимума.

анаконда против змије питона

Решење: Техника враћања уназад може бити решење локалног максимума у ​​пејзажу простора стања. Направите листу обећавајућих путања тако да алгоритам може да се врати назад у простор за претрагу и истражи и друге путање.

2. Плато: Плато је равна област простора за претрагу у којој сва суседна стања тренутног стања садрже исту вредност, јер овај алгоритам не налази најбољи правац за кретање. Потрага за пењање по брду може бити изгубљена у области висоравни.

Решење: Решење за плато је да се у потрази за великим корацима или врло малим корацима реши проблем. Насумично изаберите стање које је далеко од тренутног стања тако да је могуће да алгоритам пронађе област која није висоравни.

3. Гребени: Гребен је посебан облик локалног максимума. Има површину која је виша од околних подручја, али сама има нагиб и до ње се не може доћи једним потезом.

Решење: Коришћењем двосмерне претраге, или кретањем у различитим правцима, можемо побољшати овај проблем.

Симулирано жарење:

Алгоритам за пењање по брду који никада не иде ка нижој вредности гарантовано је непотпун јер се може заглавити на локалном максимуму. А ако алгоритам примени насумично ходање, померањем наследника, онда може да се заврши, али не и ефикасан. Симулирано жарење је алгоритам који даје и ефикасност и потпуност.

У механичком смислу Жарење је процес очвршћавања метала или стакла до високе температуре, а затим постепеног хлађења, тако да то омогућава металу да достигне нискоенергетско кристално стање. Исти процес се користи у симулираном жарењу у коме алгоритам бира насумичан потез, уместо да бира најбољи потез. Ако насумични потез побољшава стање, онда иде истим путем. У супротном, алгоритам прати путању која има вероватноћу мању од 1 или се креће низбрдо и бира другу путању.