Похлепни метод је једна од стратегија попут Завади па владај која се користи за решавање проблема. Овај метод се користи за решавање проблема оптимизације. Проблем оптимизације је проблем који захтева или максималне или минималне резултате. Хајде да разумемо кроз неке појмове.
Грееди метода је најједноставнији и најједноставнији приступ. То није алгоритам, али јесте техника. Главна функција овог приступа је да се одлука доноси на основу тренутно доступних информација. Какве год да су тренутне информације присутне, одлука се доноси без бриге о ефектима тренутне одлуке у будућности.
алгоритам брзог сортирања
Ова техника се у основи користи за одређивање изводљивог решења које може или не мора бити оптимално. Изводљиво решење је подскуп који задовољава дате критеријуме. Оптимално решење је решење које је најбоље и најповољније решење у подскупу. У случају изводљивог, ако више од једног решења задовољава дате критеријуме онда ће се та решења сматрати изводљивим, док је оптимално решење најбоље решење међу свим решењима.
Карактеристике Грееди методе
Следеће су карактеристике похлепне методе:
- Да би се решење конструисало на оптималан начин, овај алгоритам креира два скупа где један скуп садржи све изабране ставке, а други скуп садржи одбачене ставке.
- Алгоритам Грееди прави добре локалне изборе у нади да би решење требало да буде или изводљиво или оптимално.
Компоненте Грееди алгоритма
Компоненте које се могу користити у похлепном алгоритму су:
десц табела у мискл
Примене похлепног алгоритма
- Користи се за проналажење најкраћег пута.
- Користи се за проналажење минималног разапињућег стабла користећи прим алгоритам или Крускалов алгоритам.
- Користи се у редоследу послова са роком.
- Овај алгоритам се такође користи за решавање проблема фракционог ранца.
Псеудо код похлепног алгоритма
Algorithm Greedy (a, n) { Solution : = 0; for i = 0 to n do { x: = select(a); if feasible(solution, x) { Solution: = union(solution , x) } return solution; } } Горе наведени је похлепни алгоритам. У почетку, решењу се додељује нула вредност. Проследимо низ и број елемената у похлепном алгоритму. Унутар петље фор бирамо један по један елемент и проверавамо да ли је решење изводљиво или не. Ако је решење изводљиво, онда вршимо унију.
Хајде да разумемо кроз пример.
Претпоставимо да постоји проблем 'П'. Желим да путујем од А до Б приказаног испод:
П : А → Б
Проблем је у томе што морамо да путујемо овим путовањем од А до Б. Постоје различита решења да идемо од А до Б. Можемо да идемо од А до Б тако што шетња, ауто, бицикл, воз, авион , итд. Постоји ограничење у путовању да морамо прећи ово путовање у року од 12 сати. Само ако идем возом или авионом, ову удаљеност могу прећи у року од 12 сати. Постоји много решења за овај проблем, али постоје само два решења која задовољавају ограничење.
Ако кажемо да морамо покрити пут уз минималне трошкове. То значи да морамо прећи ову удаљеност што је могуће минимално, тако да је овај проблем познат као проблем минимизације. До сада имамо два изводљива решења, једно возом и друго ваздухом. Пошто ће путовање возом довести до минималних трошкова па је то оптимално решење. Оптимално решење је и изводљиво решење, али пружа најбољи резултат тако да је то решење оптимално решење са минималним трошковима. Постојало би само једно оптимално решење.
Проблем који захтева минимални или максимални резултат тада је познат као проблем оптимизације. Грееди метода је једна од стратегија која се користи за решавање проблема оптимизације.
вештачка интелигенција и интелигентни агенти
Недостаци коришћења Грееди алгоритма
Похлепни алгоритам доноси одлуке на основу информација доступних у свакој фази без разматрања ширег проблема. Дакле, може постојати могућност да похлепно решење не даје најбоље решење за сваки проблем.
Она прати избор локалног оптимума у свакој фази са намером да се пронађе глобални оптимум. Хајде да разумемо кроз пример.
Размотрите графикон који је дат у наставку:
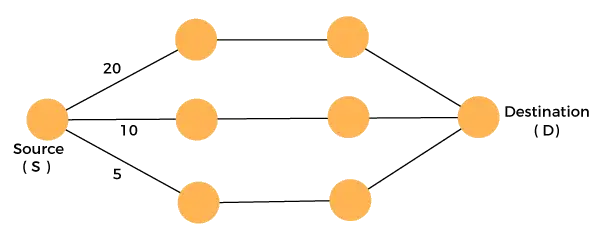
Морамо путовати од извора до одредишта уз минималне трошкове. Пошто имамо три изводљива решења која имају путање трошкова као 10, 20 и 5. 5 је пут минималних трошкова тако да је оптимално решење. Ово је локални оптимум и на тај начин налазимо локални оптимум у свакој фази да бисмо израчунали глобално оптимално решење.
јава како заобићи
