У овом одељку ћемо разговарати о методу претварања НФА у његов еквивалентни ДФА. У НФА, када се одређени улаз да у тренутно стање, машина прелази у више стања. Може имати нула, један или више потеза на датом улазном симболу. С друге стране, у ДФА, када се специфичан улаз да у тренутно стање, машина прелази у само једно стање. ДФА има само један потез на датом улазном симболу.
Нека је М = (К, ∑, δ, к0, Ф) НФА која прихвата језик Л(М). Требало би да постоји еквивалентна ДФА означена са М' = (К', ∑', к0', δ', Ф') тако да је Л(М) = Л(М').
Кораци за претварање НФА у ДФА:
Корак 1: У почетку К' = ϕ
Корак 2: Додајте к0 НФА у К'. Затим пронађите прелазе из овог почетног стања.
Корак 3: У К' пронађите могући скуп стања за сваки улазни симбол. Ако овај скуп стања није у К', додајте га у К'.
јава стринг цмп
4. корак: У ДФА, коначно стање ће бити сва стања која садрже Ф (коначна стања НФА)
Пример 1:
Конвертујте дати НФА у ДФА.
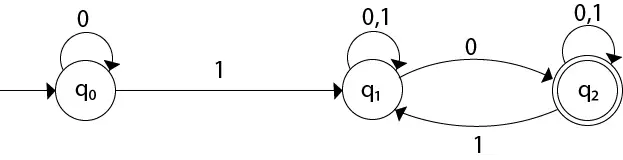
Решење: За дати дијаграм прелаза прво ћемо конструисати прелазну табелу.
| Држава | 0 | 1 |
|---|---|---|
| →к0 | к0 | к1 |
| к1 | {к1, к2} | к1 |
| *к2 | к2 | {к1, к2} |
Сада ћемо добити δ' прелаз за стање к0.
стринг ти инт
δ'([q0], 0) = [q0] δ'([q0], 1) = [q1]
δ' прелаз за стање к1 се добија као:
δ'([q1], 0) = [q1, q2] (new state generated) δ'([q1], 1) = [q1]
δ' прелаз за стање к2 се добија као:
δ'([q2], 0) = [q2] δ'([q2], 1) = [q1, q2]
Сада ћемо добити δ' прелаз на [к1, к2].
δ'([q1, q2], 0) = δ(q1, 0) ∪ δ(q2, 0) = {q1, q2} ∪ {q2} = [q1, q2] δ'([q1, q2], 1) = δ(q1, 1) ∪ δ(q2, 1) = {q1} ∪ {q1, q2} = {q1, q2} = [q1, q2] Стање [к1, к2] је такође коначно стање јер садржи коначно стање к2. Прелазна табела за изграђени ДФА ће бити:
почиње са јава
| Држава | 0 | 1 |
|---|---|---|
| →[к0] | [к0] | [к1] |
| [к1] | [к1, к2] | [к1] |
| *[к2] | [к2] | [к1, к2] |
| *[к1, к2] | [к1, к2] | [к1, к2] |
Дијаграм транзиције ће бити:

Стање к2 се може елиминисати јер је к2 недостижно стање.
Пример 2:
Конвертујте дати НФА у ДФА.

Решење: За дати дијаграм прелаза прво ћемо конструисати прелазну табелу.
апплет апплет
| Држава | 0 | 1 |
|---|---|---|
| →к0 | {к0, к1} | {к1} |
| *к1 | ϕ | {к0, к1} |
Сада ћемо добити δ' прелаз за стање к0.
δ'([q0], 0) = {q0, q1} = [q0, q1] (new state generated) δ'([q0], 1) = {q1} = [q1] δ' прелаз за стање к1 се добија као:
δ'([q1], 0) = ϕ δ'([q1], 1) = [q0, q1]
Сада ћемо добити δ' прелаз на [к0, к1].
δ'([q0, q1], 0) = δ(q0, 0) ∪ δ(q1, 0) = {q0, q1} ∪ ϕ = {q0, q1} = [q0, q1] Слично,
δ'([q0, q1], 1) = δ(q0, 1) ∪ δ(q1, 1) = {q1} ∪ {q0, q1} = {q0, q1} = [q0, q1] Као у датом НФА, к1 је коначно стање, онда у ДФА где год постоји к1 то стање постаје коначно стање. Стога су у ДФА коначна стања [к1] и [к0, к1]. Дакле, скуп коначних стања Ф = {[к1], [к0, к1]}.
листе латекса
Прелазна табела за изграђени ДФА ће бити:
| Држава | 0 | 1 |
|---|---|---|
| →[к0] | [к0, к1] | [к1] |
| *[к1] | ϕ | [к0, к1] |
| *[к0, к1] | [к0, к1] | [к0, к1] |
Дијаграм транзиције ће бити:

Чак и ми можемо да променимо назив држава ДФА.
Претпоставимо
A = [q0] B = [q1] C = [q0, q1]
Са овим новим именима ДФА ће бити следећа:

