- Битвисе КСОР оператор је такође познат као Ексклузивно ОР
- Означава се коришћењем '^'
- Као што назив показује, ради на битни ниво од операнда.
- Битвисе КСОР оператор је дошао у категорију Битвисе оператора.
- У битовом ексклузивном ОР оператору (КСОР), два операнда су потребна, а ова два операнда су одвојена КСОР симболом, тј. '^'.
- Да бисмо одредили излаз или резултат који излази након примене КСОР оператора на два операнда, морамо да пратимо табелу логичке истинитости оператора КСОР.
- КСОР табела истине је математичка табела конструисана коришћењем одговарајуће логике КСОР оператора.
- Логика која се користи иза КСОР оператора је; кад год се операција КСОР примени на два различит битова два операнда, онда ће резултат увек произвести '1', а ако се операција КСОР примени на два исти битова два операнда онда резултат производи излаз '0'.
Табела истинитости екслузивног ОР (КСОР) оператора
Нека постоје два операнда; Први је А, а други Б, укупне комбинације улаза које формирају ова два операнда биће 4. Користећи следећу КСОР табелу истинитости, одредићемо одговарајући излаз. Резултат ће бити снимљен у Ц, овде Ц = А ^ Б.
У овој табели истинитости, унос узимамо у облику битова, тј. 0 и 1, а излаз ће такође бити генерисан у облику битова, односно 0 и 1.
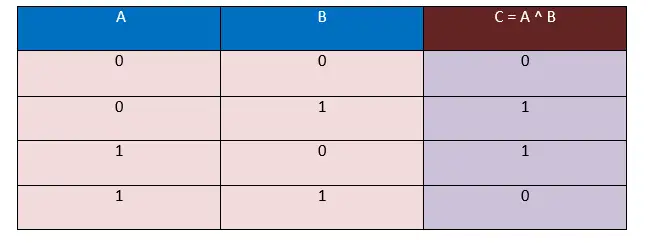
Овде, у горњој табели КСОР истине, примећујемо да када су вредности операнада А и Б различите, тј. ( 0, 1 ), ( 1, 0 ), резултат који излази увек ће бити 1. А када вредности операнада А и Б су исте, тј. ( 0, 0 ), ( 1, 1 ), резултат који излази увек ће бити 0.
Слично, на овај начин можемо нацртати табелу истине за Боолеан вредности -
Нека постоје два операнда; први је А а други је Б . Укупне комбинације улаза које формирају ова два операнда биће 4. Користећи следећу КСОР табелу истинитости, одредићемо одговарајући излаз. Резултат ће бити ухваћен у Ц, овде Ц = А ^ Б.
У овој табели истине, уносимо податке у облику вредности истине, тј. Тачно (Т) и Нетачно (Ф). Излаз ће такође бити генерисан у облику тачних вредности, тј. Т и Ф.

Овде, у горњој табели КСОР истине, примећујемо да, када су вредности операнада А и Б различите, тј. (Ф, Т), (Т, Ф), резултат ће увек бити Т. А када вредности операнада А и Б су исте, тј. (Ф, Ф), (Т, Т), резултат ће увек бити Ф.
Из горњих табела то примећујемо Т (Тачно) је означено са један, а Ф (Нетачно) је означено са 0.
Кораци за решавање било ког проблема -
- Операнди дати у задатку ће увек бити у децималној вредности.
- Прво, морамо да конвертујемо вредности операнада у бинарни
- Након претварања вредности операнада у бинарне бројеве, ставите оба операнда један преко другог.
- Запамтите да пре него што примените искључиву операцију ИЛИ (КСОР) на њих, љубазно проверите број цифара у њима.
- Ако се број цифара не поклапа, додатне нуле на левом крају малог операнда уравнотежују број цифара.
- Коначно, уз помоћ горње табеле истинитости, примените операцију КСОР на операнде један по један, узимајући један по један бит за примену операције КСОР.
- Коначно, резултат се производи у облику оутпута.
- Произведени излаз ће бити у бинарном облику, сада претворите бинарни облик у децимални облик и забележите вредност резултата.
Извршавање операције искључивог битног ИЛИ (КСОР) у Ц++
Хајде да разумемо детаљније о извршавању КСОР операције у Ц++ уз помоћ примера -
Пример 1: Пронађите ексклузивно ИЛИ целобројних вредности; 10 и 14. Такође, објасните то и напишите код извршења у Ц++.
Решење: Размотримо две променљиве, 'а ' и 'б', да ускладиштимо одговарајућа два операнда дата у горњем питању, тј. 10 и 14.
Овде је а = 10 и б = 14.
Пратићемо доле наведене кораке да бисмо сазнали ексклузивно ОР за дата два операнда.
- Знамо да су 10 и 14 у децималном облику, а за примену битне операције КСОР потребно је конвертовати у бинарни облик.
- Бинарни облик 'а', тј. 10 је '1010' и бинарни облик 'б', тј. 14 је '1110'.
- Овде примећујемо да је број бинарних цифара присутних у а четири и да је број бинарних цифара присутних у б такође 4; стога је број бинарних цифара присутних у обе променљиве исти и већ избалансиран, не морамо да додајемо више нула да бисмо га уравнотежили.
- Сада, спуштамо бинарне цифре присутне у 'б' на бинарне цифре присутне у 'а'.
- Коначно, примена КСОР операције један по један на одговарајуће битове одговара и бележи излаз.
- Коначно генерисани излаз ће бити у бинарном облику, као што је горње питање дато у децималном облику, тако да морамо да конвертујемо резултат у децимални облик.
Објашњење:
а = 10 ( у децималном облику )
б = 14 ( у децималном облику )
Сада, за КСОР б, морамо да конвертујемо а и б у бинарном облику -
мапа вс сет
а = 1010 ( у бинарном облику )
б = 1110 ( у бинарном облику )
Сада, примењујући КСОР операцију на а и б -
а = 1010
б = 1110
---------------
а ^ б = 0100 (У бинарном облику)
Резултат а ^ б је 0100, који је у бинарном облику.
Сада претварамо резултат у децимални облик, а то је 4.
10^14 = 4
НАПОМЕНА: Коришћењем горње табеле истинитости КСОР, генеришу се излазни подаци одговарајућих битова.
Сада ћемо применити операцију КСОР у битовима на 10 и 14 у језику Ц++ и добити резултат, тј., 4.
Ц++ код за горњи пример:
//************************ C++ Code ****************************** #include using namespace std; int main () { int a, b, c ; // Initializing integer variables to store data values cout <' << endl ; cout <> a ; // taking a as input from user cout <> b ; // taking b as input from user c = a ^ b ; // storing XOR result of a and b in c cout << 'Applying XOR operation on a and b: '<< endl ; cout << 'a ^ b = ' << c << endl ; // Printing the output } </'> Излаз

Пример 2: Пронађите ексклузивно ИЛИ целобројних вредности; 3 и 15. Такође, објасните то и напишите код извршења у Ц++.
Решење: Размотримо две променљиве, ' а ' и ' б ', да ускладиштимо одговарајућа два операнда дата у горњем питању, тј. 3 и 15.
Овде је а = 3 и б = 15.
претворити цхар у стринг
Пратићемо доле наведене кораке да бисмо сазнали ексклузивно ОР за дата два операнда.
- Знамо да су 3 и 15 у децималном облику, а за примену битне операције КСОР потребно је да се конвертује у бинарни облик.
- Бинарни облик 'а', тј. 3 је 'Једанаест' и бинарни облик 'б', тј. 15 је '1111'.
- Овде ћемо приметити да је број бинарних цифара присутних у а два и да је број бинарних цифара присутних у б четири; стога број бинарних цифара присутних у обе променљиве није исти. Стога, неуравнотежено, морамо додати још број 0 на левој страни доњег бинарног броја, тј. а, што је ' Једанаест' , да га уравнотежите.
- Након балансирања, вредност а је '0011' , и б је '1111'.
- Сада, спуштамо бинарне цифре присутне у 'б' на бинарне цифре присутне у 'а'.
- Коначно, примена КСОР операције један по један на одговарајуће битове одговара и бележи излаз.
- Коначно генерисани излаз ће бити у бинарном облику, као што је горње питање дато у децималном облику, тако да морамо да конвертујемо резултат у децимални облик.
Објашњење:
а = 3 ( у децималном облику )
б = 15 ( у децималном облику )
Сада, за КСОР б, морамо да конвертујемо а и б у бинарном облику -
а = 0011 ( у бинарном облику )
б = 1111 ( у бинарном облику )
Сада, примењујући КСОР операцију на а и б -
а = 0011
б = 1111
---------------
а ^ б = 1100 (У бинарном облику)
Резултат а ^ б је 1100, што је у бинарном облику.
Сада претварамо резултат у децимални облик, који је 12.
3^15 = 12
НАПОМЕНА: Коришћењем горње табеле истинитости КСОР, генеришу се излазни подаци одговарајућих битова.
Сада ћемо применити битну операцију КСОР на 3 и 15 у језику Ц++ и добити резултат, тј., 12.
Ц++ код за горњи пример:
//************************ C++ Code ****************************** #include using namespace std; int main () { int a, b, c ; // Initializing integer variables to store data values cout <' << endl ; cout <> a ; // taking a as input from user cout <> b ; // taking b as input from user c = a ^ b ; // storing XOR result of a and b in c cout << 'Applying XOR operation on a and b: '<< endl ; cout << 'a ^ b = ' << c << endl ; // Printing the output } </'> Излаз

