Машинско учење је грана вештачке интелигенције, која омогућава машинама да врше анализу података и предвиђају. Међутим, ако модел машинског учења није тачан, може направити грешке у предвиђању, а ове грешке предвиђања су обично познате као пристрасност и варијанса. У машинском учењу, ове грешке ће увек бити присутне јер увек постоји мала разлика између предвиђања модела и стварних предвиђања. Главни циљ аналитичара МЛ/науке о подацима је да смање ове грешке како би добили тачније резултате. У овој теми ћемо разговарати о пристрасности и варијанси, компромису пристрасности и варијансе, недовољно уградњи и преоптерећењу. Али пре него што почнемо, хајде да прво разумемо које су грешке у машинском учењу?
Грешке у машинском учењу?
У машинском учењу, грешка је мера колико тачно алгоритам може да направи предвиђања за претходно непознати скуп података. На основу ових грешака, бира се модел машинског учења који може најбоље да ради на одређеном скупу података. Постоје углавном две врсте грешака у машинском учењу, а то су:

без обзира на то који је алгоритам коришћен. Узрок ових грешака су непознате променљиве чија се вредност не може смањити.
Шта је пристрасност?
Генерално, модел машинског учења анализира податке, проналази обрасце у њима и прави предвиђања. Током обуке, модел учи ове обрасце у скупу података и примењује их на податке тестирања ради предвиђања. Приликом предвиђања долази до разлике између вредности предвиђања које је направио модел и стварних вредности/очекиваних вредности , а ова разлика је позната као грешке пристрасности или грешке због пристрасности . Може се дефинисати као неспособност алгоритама за машинско учење као што је линеарна регресија да ухвати прави однос између тачака података. Сваки алгоритам почиње са одређеном количином пристрасности јер пристрасност настаје из претпоставки у моделу, што циљну функцију чини једноставном за учење. Модел има или:
саира бану глумац
Генерално, линеарни алгоритам има велику пристрасност, јер их чини да брзо уче. Што је алгоритам једноставнији, већа је вероватноћа да ће бити уведен. Док нелинеарни алгоритам често има ниску пристрасност.
Неки примери алгоритама машинског учења са малом пристрасношћу су стабла одлучивања, к-најближи суседи и машине за векторе подршке . Истовремено, алгоритам са великом пристрасношћу је Линеарна регресија, линеарна дискриминантна анализа и логистичка регресија.
Начини за смањење високе пристрасности:
Велика пристрасност се углавном јавља због много једноставног модела. Испод су неки начини да се смањи велика пристрасност:
- Повећајте улазне карактеристике пошто је модел недовољно опремљен.
- Смањите рок регуларизације.
- Користите сложеније моделе, као што је укључивање неких полиномских карактеристика.
Шта је грешка варијансе?
Варијанца би специфицирала количину варијације у предвиђању ако би се користили различити подаци о обуци. једноставним речима, варијанса говори колико се случајна променљива разликује од њене очекиване вредности. У идеалном случају, модел не би требало превише да варира од једног скупа података за обуку до другог, што значи да би алгоритам требало да буде добар у разумевању скривеног мапирања између улазних и излазних варијабли. Грешке варијансе су било које од њих мала варијанса или висока варијанса.
тигар лав разлика
Мала варијанса значи да постоји мала варијација у предвиђању циљне функције са променама у скупу података за обуку. Истовремено, Висока варијанса показује велику варијацију у предвиђању циљне функције са променама у скупу података за обуку.
Модел који показује велику варијансу много учи и добро ради са скупом података за обуку, а не генерализује се добро са невидљивим скупом података. Као резултат тога, такав модел даје добре резултате са скупом података за обуку, али показује високе стопе грешака у скупу података теста.
Пошто, са великом варијансом, модел превише учи из скупа података, то доводи до преоптерећења модела. Модел са великом варијансом има следеће проблеме:
- Модел велике варијансе доводи до претеривања.
- Повећајте сложеност модела.
Обично нелинеарни алгоритми имају велику флексибилност да се уклопе у модел, имају велику варијансу.

Неки примери алгоритама машинског учења са малом варијансом су, Линеарна регресија, логистичка регресија и линеарна дискриминантна анализа . Истовремено, алгоритми са великом варијансом су дрво одлучивања, машина за подршку векторима и К-најближи суседи.
инкапсулација у јава
Начини да се смањи велика варијанса:
- Смањите улазне карактеристике или број параметара пошто је модел превише опремљен.
- Немојте користити много сложен модел.
- Повећајте податке о обуци.
- Повећајте рок за регулисање.
Различите комбинације пристрасности-варијансе
Постоје четири могуће комбинације пристрасности и варијанси, које су представљене дијаграмом испод:

Комбинација ниске пристрасности и ниске варијансе показује идеалан модел машинског учења. Међутим, то практично није могуће.
Са великом пристрасношћу и великом варијансом, предвиђања су недоследна и такође у просеку нетачна.
Како препознати високу варијансу или високу пристрасност?
Велика варијанса се може идентификовати ако модел има:

- Мала грешка у тренингу и велика грешка у тесту.
Висока пристрасност се може идентификовати ако модел има:
- Велика грешка у тренингу и грешка теста је скоро слична грешци у тренингу.
Биас-Варианце Траде-Офф
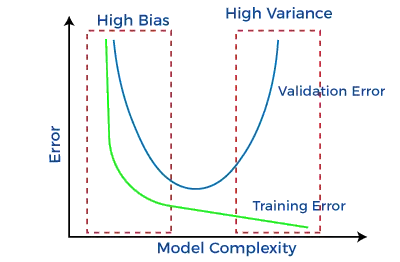
Приликом изградње модела машинског учења, заиста је важно водити рачуна о пристрасности и варијанси како би се избегло претерано и недовољно уклапање у модел. Ако је модел веома једноставан са мање параметара, може имати ниску варијансу и велику пристрасност. Док, ако модел има велики број параметара, он ће имати велику варијансу и ниску пристрасност. Дакле, потребно је направити равнотежу између грешке пристрасности и грешке варијансе, а ова равнотежа између грешке пристрасности и грешке варијансе је позната као компромис биас-варијанса.

За тачно предвиђање модела, алгоритмима је потребна ниска варијанса и мала пристрасност. Али то није могуће јер су пристрасност и варијанса међусобно повезане:
- Ако смањимо варијансу, то ће повећати пристрасност.
- Ако смањимо пристрасност, то ће повећати варијансу.
Компромис пристрасности и варијансе је централно питање у надгледаном учењу. У идеалном случају, потребан нам је модел који тачно хвата правилности у подацима о обуци и истовремено добро генерализује са невидљивим скупом података. Нажалост, ово није могуће учинити истовремено. Зато што алгоритам високе варијансе може добро да ради са подацима о обуци, али може довести до претераног прилагођавања бучним подацима. Док алгоритам високе пристрасности генерише много једноставан модел који можда чак и не обухвата важне правилности у подацима. Дакле, морамо да пронађемо слатку тачку између пристрасности и варијансе да бисмо направили оптималан модел.
Отуда Компромис пристрасности и варијансе се односи на проналажење слатке тачке за постизање равнотеже између грешака пристрасности и варијансе.
