Белман форд алгоритам је алгоритам најкраћег пута са једним извором. Овај алгоритам се користи за проналажење најкраће удаљености од једног темена до свих осталих врхова пондерисаног графа. Постоје разни други алгоритми који се користе за проналажење најкраће путање као што је Дијкстра алгоритам, итд. Ако пондерисани граф садржи негативне вредности тежине, онда Дијкстра алгоритам не потврђује да ли даје тачан одговор или не. За разлику од Дијкстра алгоритма, алгоритам Беллман Форд гарантује тачан одговор чак и ако пондерисани граф садржи негативне вредности тежине.
Правило овог алгоритма
We will go on relaxing all the edges (n - 1) times where, n = number of vertices
Размотрите доњи графикон:
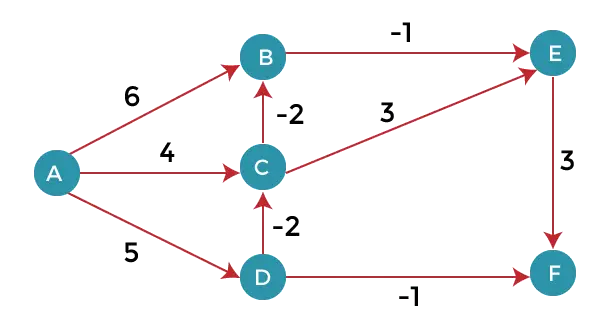
Као што можемо приметити на горњем графикону да су неке тежине негативне. Горњи граф садржи 6 врхова тако да ћемо наставити да опуштамо до 5 врхова. Овде ћемо опустити све ивице 5 пута. Петља ће поновити 5 пута да би добила тачан одговор. Ако се петља понови више од 5 пута, онда ће и одговор бити исти, тј. не би било промене у растојању између врхова.
Опуштање значи:
'која је разлика између лава и тигра'
If (d(u) + c(u , v) <d(v)) d(v)="d(u)" + c(u , v) < pre> <p>To find the shortest path of the above graph, the first step is note down all the edges which are given below:</p> <p>(A, B), (A, C), (A, D), (B, E), (C, E), (D, C), (D, F), (E, F), (C, B)</p> <p>Let's consider the source vertex as 'A'; therefore, the distance value at vertex A is 0 and the distance value at all the other vertices as infinity shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-2.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph has six vertices so it will have five iterations.</p> <p> <strong>First iteration</strong> </p> <p>Consider the edge (A, B). Denote vertex 'A' as 'u' and vertex 'B' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 6</p> <p>Since (0 + 6) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 6 = 6</p> <p>Therefore, the distance of vertex B is 6.</p> <p>Consider the edge (A, C). Denote vertex 'A' as 'u' and vertex 'C' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex C is 4.</p> <p>Consider the edge (A, D). Denote vertex 'A' as 'u' and vertex 'D' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex D is 5.</p> <p>Consider the edge (B, E). Denote vertex 'B' as 'u' and vertex 'E' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 6</p> <p>d(v) = ∞</p> <p>c(u , v) = -1</p> <p>Since (6 - 1) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 6 - 1= 5</p> <p>Therefore, the distance of vertex E is 5.</p> <p>Consider the edge (C, E). Denote vertex 'C' as 'u' and vertex 'E' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 4</p> <p>d(v) = 5</p> <p>c(u , v) = 3</p> <p>Since (4 + 3) is greater than 5, so there will be no updation. The value at vertex E is 5.</p> <p>Consider the edge (D, C). Denote vertex 'D' as 'u' and vertex 'C' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = -2</p> <p>Since (5 -2) is less than 4, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 5 - 2 = 3</p> <p>Therefore, the distance of vertex C is 3.</p> <p>Consider the edge (D, F). Denote vertex 'D' as 'u' and vertex 'F' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = ∞</p> <p>c(u , v) = -1</p> <p>Since (5 -1) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 5 - 1 = 4</p> <p>Therefore, the distance of vertex F is 4.</p> <p>Consider the edge (E, F). Denote vertex 'E' as 'u' and vertex 'F' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = ∞</p> <p>c(u , v) = 3</p> <p>Since (5 + 3) is greater than 4, so there would be no updation on the distance value of vertex F.</p> <p>Consider the edge (C, B). Denote vertex 'C' as 'u' and vertex 'B' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 3</p> <p>d(v) = 6</p> <p>c(u , v) = -2</p> <p>Since (3 - 2) is less than 6, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 3 - 2 = 1</p> <p>Therefore, the distance of vertex B is 1.</p> <p>Now the first iteration is completed. We move to the second iteration.</p> <p> <strong>Second iteration:</strong> </p> <p>In the second iteration, we again check all the edges. The first edge is (A, B). Since (0 + 6) is greater than 1 so there would be no updation in the vertex B.</p> <p>The next edge is (A, C). Since (0 + 4) is greater than 3 so there would be no updation in the vertex C.</p> <p>The next edge is (A, D). Since (0 + 5) equals to 5 so there would be no updation in the vertex D.</p> <p>The next edge is (B, E). Since (1 - 1) equals to 0 which is less than 5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(E) = d(B) +c(B , E)</p> <p>= 1 - 1 = 0</p> <p>The next edge is (C, E). Since (3 + 3) equals to 6 which is greater than 5 so there would be no updation in the vertex E.</p> <p>The next edge is (D, C). Since (5 - 2) equals to 3 so there would be no updation in the vertex C.</p> <p>The next edge is (D, F). Since (5 - 1) equals to 4 so there would be no updation in the vertex F.</p> <p>The next edge is (E, F). Since (5 + 3) equals to 8 which is greater than 4 so there would be no updation in the vertex F.</p> <p>The next edge is (C, B). Since (3 - 2) equals to 1` so there would be no updation in the vertex B.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-3.webp" alt="Bellman-Ford Algorithm"> <p> <strong>Third iteration</strong> </p> <p>We will perform the same steps as we did in the previous iterations. We will observe that there will be no updation in the distance of vertices.</p> <pre> The following are the distances of vertices: A: 0 B: 1 C: 3 D: 5 E: 0 F: 3 </pre> <p> <strong>Time Complexity</strong> </p> <p>The time complexity of Bellman ford algorithm would be O(E|V| - 1).</p> <pre> function bellmanFord(G, S) for each vertex V in G distance[V] <- 0 infinite previous[v] <- null distance[s] for each vertex v in g edge (u,v) tempdistance distance[u] + edge_weight(u, v) if < distance[v] u distance[v} error: negative cycle exists return distance[], previous[] pre> <p> <strong>Drawbacks of Bellman ford algorithm</strong> </p> <ul> <li>The bellman ford algorithm does not produce a correct answer if the sum of the edges of a cycle is negative. Let's understand this property through an example. Consider the below graph. <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-4.webp" alt="Bellman-Ford Algorithm"></li> <li>In the above graph, we consider vertex 1 as the source vertex and provides 0 value to it. We provide infinity value to other vertices shown as below: <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-5.webp" alt="Bellman-Ford Algorithm"> <br>Edges can be written as: <br> (1, 3), (1, 2), (2, 4), (3, 2), (4, 3) </li> </ul> <p> <strong>First iteration</strong> </p> <p> <strong>Consider the edge (1, 3). Denote vertex '1' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex 3 is 5.</p> <p> <strong>Consider the edge (1, 2). Denote vertex '1' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex 2 is 4.</p> <p> <strong>Consider the edge (3, 2). Denote vertex '3' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = 7</p> <p>Since (5 + 7) is greater than 4, so there would be no updation in the vertex 2.</p> <p> <strong>Consider the edge (2, 4). Denote vertex '2' as 'u' and vertex '4' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 4</p> <p>d(v) = ∞</p> <p>c(u , v) = 7</p> <p>Since (4 + 7) equals to 11 which is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 4 + 7 = 11</p> <p>Therefore, the distance of vertex 4 is 11.</p> <p> <strong>Consider the edge (4, 3). Denote vertex '4' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 11</p> <p>d(v) = 5</p> <p>c(u , v) = -15</p> <p>Since (11 - 15) equals to -4 which is less than 5, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 11 - 15 = -4</p> <p>Therefore, the distance of vertex 3 is -4.</p> <p>Now we move to the second iteration.</p> <p> <strong>Second iteration</strong> </p> <p>Now, again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -4 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-4 + 7) equals to 3 which is less than 4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -4 + 7 = 3</p> <p>Therefore, the value at vertex 2 is 3.</p> <p>The next edge is (2, 4). Since ( 3+7) equals to 10 which is less than 11 so update</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 3 + 7 = 10</p> <p>Therefore, the value at vertex 4 is 10.</p> <p>The next edge is (4, 3). Since (10 - 15) equals to -5 which is less than -4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 10 - 15 = -5</p> <p>Therefore, the value at vertex 3 is -5.</p> <p>Now we move to the third iteration.</p> <p> <strong>Third iteration</strong> </p> <p>Now again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -5 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 which is greater than 3 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-5 + 7) equals to 2 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -5 + 7 = 2</p> <p>Therefore, the value at vertex 2 is 2.</p> <p>The next edge is (2, 4). Since (2 + 7) equals to 9 which is less than 10 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 2 + 7 = 9</p> <p>Therefore, the value at vertex 4 is 9.</p> <p>The next edge is (4, 3). Since (9 - 15) equals to -6 which is less than -5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 9 - 15 = -6</p> <p>Therefore, the value at vertex 3 is -6.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-6.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph contains 4 vertices, so according to the bellman ford algorithm, there would be only 3 iterations. If we try to perform 4<sup>th</sup> iteration on the graph, the distance of the vertices from the given vertex should not change. If the distance varies, it means that the bellman ford algorithm is not providing the correct answer.</p> <p> <strong>4<sup>th</sup> iteration</strong> </p> <p>The first edge is (1, 3). Since (0 +5) equals to 5 which is greater than -6 so there would be no change in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) is greater than 2 so there would be no updation.</p> <p>The next edge is (3, 2). Since (-6 + 7) equals to 1 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -6 + 7 = 1</p> <p>In this case, the value of the vertex is updated. So, we conclude that the bellman ford algorithm does not work when the graph contains the negative weight cycle.</p> <p>Therefore, the value at vertex 2 is 1.</p> <hr></-></pre></d(v))>
д(в) = 0 + 6 = 6
Дакле, растојање темена Б је 6.
Размотримо ивицу (А, Ц). Означимо врх 'А' као 'у' и врх 'Ц' као 'в'. Сада користите опуштајућу формулу:
д(у) = 0
д(в) = ∞
ц(у, в) = 4
Пошто је (0 + 4) мање од ∞, ажурирајте
d(v) = d(u) + c(u , v)
д(в) = 0 + 4 = 4
Дакле, растојање темена Ц је 4.
Размотримо ивицу (А, Д). Означимо врх 'А' као 'у' и врх 'Д' као 'в'. Сада користите опуштајућу формулу:
д(у) = 0
д(в) = ∞
ц(у, в) = 5
Пошто је (0 + 5) мање од ∞, ажурирајте
d(v) = d(u) + c(u , v)
д(в) = 0 + 5 = 5
Дакле, растојање темена Д је 5.
Размотримо ивицу (Б, Е). Означимо врх 'Б' као 'у', а врх 'Е' као 'в'. Сада користите опуштајућу формулу:
д(у) = 6
д(в) = ∞
ц(у, в) = -1
Пошто је (6 - 1) мање од ∞, ажурирајте
d(v) = d(u) + c(u , v)
д(в) = 6 - 1= 5
Дакле, растојање темена Е је 5.
Размотримо ивицу (Ц, Е). Означимо врх 'Ц' као 'у' и врх 'Е' као 'в'. Сада користите опуштајућу формулу:
д(у) = 4
д(в) = 5
ц(у, в) = 3
Пошто је (4 + 3) веће од 5, неће бити ажурирања. Вредност на врху Е је 5.
Размотримо ивицу (Д, Ц). Означимо врх 'Д' као 'у' и 'Ц' као 'в'. Сада користите опуштајућу формулу:
д(у) = 5
д(в) = 4
ц(у, в) = -2
Пошто је (5 -2) мање од 4, ажурирајте
d(v) = d(u) + c(u , v)
д(в) = 5 - 2 = 3
Дакле, растојање темена Ц је 3.
Размотримо ивицу (Д, Ф). Означимо врх 'Д' као 'у' и 'Ф' као 'в'. Сада користите опуштајућу формулу:
д(у) = 5
д(в) = ∞
ц(у, в) = -1
Пошто је (5 -1) мање од ∞, ажурирајте
d(v) = d(u) + c(u , v)
д(в) = 5 - 1 = 4
Дакле, растојање темена Ф је 4.
како дереференцирати показивач у ц
Размотримо ивицу (Е, Ф). Означимо врх 'Е' као 'у' и врх 'Ф' као 'в'. Сада користите опуштајућу формулу:
д(у) = 5
д(в) = ∞
ц(у, в) = 3
Пошто је (5 + 3) веће од 4, не би било ажурирања вредности удаљености темена Ф.
Размотримо ивицу (Ц, Б). Означимо врх 'Ц' као 'у' и врх 'Б' као 'в'. Сада користите опуштајућу формулу:
д(у) = 3
д(в) = 6
ц(у, в) = -2
Пошто је (3 - 2) мање од 6, ажурирајте
d(v) = d(u) + c(u , v)
д(в) = 3 - 2 = 1
Према томе, растојање темена Б је 1.
Сада је прва итерација завршена. Прелазимо на другу итерацију.
Друга итерација:
У другој итерацији, поново проверавамо све ивице. Прва ивица је (А, Б). Пошто је (0 + 6) веће од 1, не би било ажурирања у темену Б.
Следећа ивица је (А, Ц). Пошто је (0 + 4) веће од 3 тако да не би било ажурирања у темену Ц.
Следећа ивица је (А, Д). Пошто је (0 + 5) једнако 5, не би било ажурирања у темену Д.
Следећа ивица је (Б, Е). Пошто је (1 - 1) једнако 0 што је мање од 5, ажурирајте:
д(в) = д(у) + ц(у, в)
д(Е) = д(Б) +ц(Б, Е)
= 1 - 1 = 0
Следећа ивица је (Ц, Е). Пошто је (3 + 3) једнако 6 што је веће од 5, тако да не би било ажурирања у темену Е.
Следећа ивица је (Д, Ц). Пошто је (5 - 2) једнако 3, не би било ажурирања у темену Ц.
Следећа ивица је (Д, Ф). Пошто је (5 - 1) једнако 4, тако да не би било ажурирања у темену Ф.
Следећа ивица је (Е, Ф). Пошто је (5 + 3) једнако 8 што је веће од 4, тако да не би било ажурирања у темену Ф.
Следећа ивица је (Ц, Б). Пошто је (3 - 2) једнако 1` тако да не би било ажурирања у темену Б.

Трећа итерација
Извршићемо исте кораке као што смо радили у претходним итерацијама. Приметићемо да неће бити ажурирања у удаљености врхова.
The following are the distances of vertices: A: 0 B: 1 C: 3 D: 5 E: 0 F: 3
Временска сложеност
Временска сложеност Беллман фордовог алгоритма би била О(Е|В| - 1).
function bellmanFord(G, S) for each vertex V in G distance[V] <- 0 infinite previous[v] <- null distance[s] for each vertex v in g edge (u,v) tempdistance distance[u] + edge_weight(u, v) if < distance[v] u distance[v} error: negative cycle exists return distance[], previous[] pre> <p> <strong>Drawbacks of Bellman ford algorithm</strong> </p> <ul> <li>The bellman ford algorithm does not produce a correct answer if the sum of the edges of a cycle is negative. Let's understand this property through an example. Consider the below graph. <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-4.webp" alt="Bellman-Ford Algorithm"></li> <li>In the above graph, we consider vertex 1 as the source vertex and provides 0 value to it. We provide infinity value to other vertices shown as below: <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-5.webp" alt="Bellman-Ford Algorithm"> <br>Edges can be written as: <br> (1, 3), (1, 2), (2, 4), (3, 2), (4, 3) </li> </ul> <p> <strong>First iteration</strong> </p> <p> <strong>Consider the edge (1, 3). Denote vertex '1' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex 3 is 5.</p> <p> <strong>Consider the edge (1, 2). Denote vertex '1' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex 2 is 4.</p> <p> <strong>Consider the edge (3, 2). Denote vertex '3' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = 7</p> <p>Since (5 + 7) is greater than 4, so there would be no updation in the vertex 2.</p> <p> <strong>Consider the edge (2, 4). Denote vertex '2' as 'u' and vertex '4' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 4</p> <p>d(v) = ∞</p> <p>c(u , v) = 7</p> <p>Since (4 + 7) equals to 11 which is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 4 + 7 = 11</p> <p>Therefore, the distance of vertex 4 is 11.</p> <p> <strong>Consider the edge (4, 3). Denote vertex '4' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 11</p> <p>d(v) = 5</p> <p>c(u , v) = -15</p> <p>Since (11 - 15) equals to -4 which is less than 5, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 11 - 15 = -4</p> <p>Therefore, the distance of vertex 3 is -4.</p> <p>Now we move to the second iteration.</p> <p> <strong>Second iteration</strong> </p> <p>Now, again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -4 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-4 + 7) equals to 3 which is less than 4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -4 + 7 = 3</p> <p>Therefore, the value at vertex 2 is 3.</p> <p>The next edge is (2, 4). Since ( 3+7) equals to 10 which is less than 11 so update</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 3 + 7 = 10</p> <p>Therefore, the value at vertex 4 is 10.</p> <p>The next edge is (4, 3). Since (10 - 15) equals to -5 which is less than -4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 10 - 15 = -5</p> <p>Therefore, the value at vertex 3 is -5.</p> <p>Now we move to the third iteration.</p> <p> <strong>Third iteration</strong> </p> <p>Now again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -5 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 which is greater than 3 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-5 + 7) equals to 2 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -5 + 7 = 2</p> <p>Therefore, the value at vertex 2 is 2.</p> <p>The next edge is (2, 4). Since (2 + 7) equals to 9 which is less than 10 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 2 + 7 = 9</p> <p>Therefore, the value at vertex 4 is 9.</p> <p>The next edge is (4, 3). Since (9 - 15) equals to -6 which is less than -5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 9 - 15 = -6</p> <p>Therefore, the value at vertex 3 is -6.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-6.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph contains 4 vertices, so according to the bellman ford algorithm, there would be only 3 iterations. If we try to perform 4<sup>th</sup> iteration on the graph, the distance of the vertices from the given vertex should not change. If the distance varies, it means that the bellman ford algorithm is not providing the correct answer.</p> <p> <strong>4<sup>th</sup> iteration</strong> </p> <p>The first edge is (1, 3). Since (0 +5) equals to 5 which is greater than -6 so there would be no change in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) is greater than 2 so there would be no updation.</p> <p>The next edge is (3, 2). Since (-6 + 7) equals to 1 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -6 + 7 = 1</p> <p>In this case, the value of the vertex is updated. So, we conclude that the bellman ford algorithm does not work when the graph contains the negative weight cycle.</p> <p>Therefore, the value at vertex 2 is 1.</p> <hr></->
д(в) = 0 + 5 = 5
Према томе, растојање темена 3 је 5.
Размотримо ивицу (1, 2). Означимо врх '1' као 'у' и врх '2' као 'в'. Сада користите опуштајућу формулу:
д(у) = 0
д(в) = ∞
ц(у, в) = 4
Пошто је (0 + 4) мање од ∞, ажурирајте
d(v) = d(u) + c(u , v)
д(в) = 0 + 4 = 4
Дакле, растојање темена 2 је 4.
Размотримо ивицу (3, 2). Означимо врх '3' као 'у' и врх '2' као 'в'. Сада користите опуштајућу формулу:
д(у) = 5
д(в) = 4
ц(у, в) = 7
преименујте линук директоријум
Пошто је (5 + 7) веће од 4, не би било ажурирања у темену 2.
Размотримо ивицу (2, 4). Означимо врх '2' као 'у' и врх '4' као 'в'. Сада користите опуштајућу формулу:
д(у) = 4
д(в) = ∞
ц(у, в) = 7
Пошто је (4 + 7) једнако 11 што је мање од ∞, ажурирајте
d(v) = d(u) + c(u , v)
д(в) = 4 + 7 = 11
Дакле, растојање темена 4 је 11.
Размотримо ивицу (4, 3). Означимо врх '4' као 'у' и '3' као 'в'. Сада користите опуштајућу формулу:
д(у) = 11
д(в) = 5
ц(у, в) = -15
Пошто је (11 - 15) једнако -4 што је мање од 5, ажурирајте
d(v) = d(u) + c(u , v)
д(в) = 11 - 15 = -4
Према томе, растојање темена 3 је -4.
Сада прелазимо на другу итерацију.
Друга итерација
Сада ћемо поново проверити све ивице. Прва ивица је (1, 3). Пошто је (0 + 5) једнако 5 што је веће од -4, тако да не би било ажурирања у темену 3.
Следећа ивица је (1, 2). Пошто је (0 + 4) једнако 4, тако да не би било ажурирања у темену 2.
Следећа ивица је (3, 2). Пошто је (-4 + 7) једнако 3 што је мање од 4, ажурирајте:
д(в) = д(у) + ц(у, в)
д(2) = д(3) +ц(3, 2)
= -4 + 7 = 3
Дакле, вредност на врху 2 је 3.
Следећа ивица је (2, 4). Пошто је (3+7) једнако 10 што је мање од 11, ажурирајте
д(в) = д(у) + ц(у, в)
д(4) = д(2) +ц(2, 4)
= 3 + 7 = 10
Дакле, вредност на врху 4 је 10.
пд мерге
Следећа ивица је (4, 3). Пошто је (10 - 15) једнако -5, што је мање од -4, ажурирајте:
д(в) = д(у) + ц(у, в)
д(3) = д(4) +ц(4, 3)
= 10 - 15 = -5
Према томе, вредност на врху 3 је -5.
Сада прелазимо на трећу итерацију.
Трећа итерација
Сада ћемо поново проверити све ивице. Прва ивица је (1, 3). Пошто је (0 + 5) једнако 5 што је веће од -5, тако да не би било ажурирања у темену 3.
Следећа ивица је (1, 2). Пошто је (0 + 4) једнако 4 што је веће од 3, тако да не би било ажурирања у темену 2.
Следећа ивица је (3, 2). Пошто је (-5 + 7) једнако 2 што је мање од 3, ажурирајте:
д(в) = д(у) + ц(у, в)
д(2) = д(3) +ц(3, 2)
= -5 + 7 = 2
Дакле, вредност у темену 2 је 2.
Следећа ивица је (2, 4). Пошто је (2 + 7) једнако 9 што је мање од 10, ажурирајте:
д(в) = д(у) + ц(у, в)
д(4) = д(2) +ц(2, 4)
= 2 + 7 = 9
Дакле, вредност на врху 4 је 9.
Следећа ивица је (4, 3). Пошто је (9 - 15) једнако -6, што је мање од -5, ажурирајте:
д(в) = д(у) + ц(у, в)
д(3) = д(4) +ц(4, 3)
= 9 - 15 = -6
Према томе, вредност на врху 3 је -6.

Пошто граф садржи 4 темена, па би према алгоритму Беллман Форда било само 3 итерације. Ако покушамо да изведемо 4тхитерацију на графу, растојање темена од датог темена не би требало да се мења. Ако се растојање разликује, то значи да алгоритам Беллман Форда не даје тачан одговор.
4тхитерација
Прва ивица је (1, 3). Пошто је (0 +5) једнако 5 што је веће од -6, тако да не би било промене у тјемену 3.
Следећа ивица је (1, 2). Пошто је (0 + 4) веће од 2, не би било ажурирања.
Следећа ивица је (3, 2). Пошто је (-6 + 7) једнако 1 што је мање од 3, ажурирајте:
д(в) = д(у) + ц(у, в)
д(2) = д(3) +ц(3, 2)
= -6 + 7 = 1
У овом случају, вредност темена се ажурира. Дакле, закључујемо да алгоритам Беллман Форд не ради када граф садржи циклус негативне тежине.
Дакле, вредност на врху 2 је 1.
