Рандом Форест је популаран алгоритам машинског учења који припада техници учења под надзором. Може се користити за проблеме класификације и регресије у МЛ. Заснован је на концепту ансамбл учење, што је процес од комбиновање више класификатора за решавање сложеног проблема и побољшање перформанси модела.
Као што име каже, 'Рандом Форест је класификатор који садржи одређени број стабала одлучивања о различитим подскуповима датог скупа података и узима просек да би побољшао тачност предвиђања тог скупа података.' Уместо да се ослања на једно стабло одлучивања, случајна шума узима предвиђање са сваког стабла и на основу већине гласова предвиђања, и предвиђа коначни резултат.
Већи број стабала у шуми доводи до веће прецизности и спречава проблем пренамјене.
методе низова
Доњи дијаграм објашњава рад алгоритма случајне шуме:
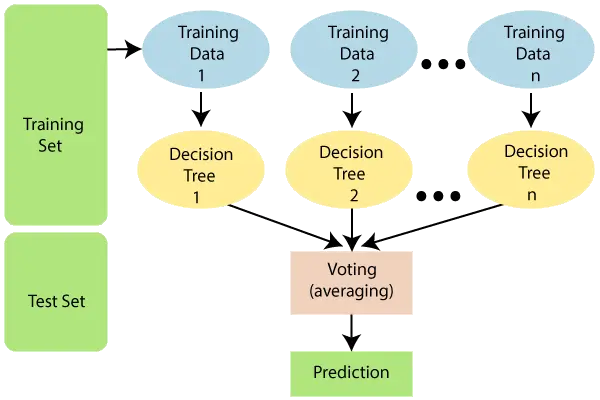
Напомена: Да бисте боље разумели алгоритам случајне шуме, требало би да знате алгоритам стабла одлучивања.
Претпоставке за случајну шуму
Пошто насумична шума комбинује више стабала да би предвидела класу скупа података, могуће је да нека стабла одлучивања могу предвидети тачан излаз, док друга не. Али заједно, сва стабла предвиђају исправан излаз. Стога, у наставку су две претпоставке за бољи класификатор случајних шума:
- Требало би да постоје неке стварне вредности у променљивој обележја скупа података тако да класификатор може да предвиди тачне резултате, а не нагађани резултат.
- Предвиђања из сваког дрвета морају имати веома ниске корелације.
Зашто користити Рандом Форест?
Испод су неке тачке које објашњавају зашто би требало да користимо алгоритам случајне шуме:
- Потребно је мање времена за обуку у поређењу са другим алгоритмима.
- Предвиђа излаз са великом прецизношћу, чак и за велики скуп података који ефикасно ради.
- Такође може да одржи тачност када недостаје велики део података.
Како функционише алгоритам случајне шуме?
Случајна шума ради у две фазе, прво је стварање случајне шуме комбиновањем Н стабла одлучивања, а друго је предвиђање за свако дрво створено у првој фази.
Радни процес се може објаснити у следећим корацима и дијаграму:
Корак 1: Изаберите случајних К тачака података из скупа за обуку.
Корак 2: Изградите стабла одлучивања повезана са изабраним тачкама података (подскупови).
Корак 3: Изаберите број Н за стабла одлука које желите да направите.
стринг јсон јава
Корак 4: Поновите корак 1 и 2.
Корак 5: За нове тачке података, пронађите предвиђања сваког стабла одлучивања и доделите нове тачке података категорији која осваја већину гласова.
Рад алгоритма може се боље разумети на следећем примеру:
Пример: Претпоставимо да постоји скуп података који садржи више слика воћа. Дакле, овај скуп података је дат класификатору случајне шуме. Скуп података је подељен на подскупове и дати сваком стаблу одлучивања. Током фазе обуке, свако стабло одлучивања производи резултат предвиђања, а када се појави нова тачка података, тада на основу већине резултата, класификатор Рандом Форест предвиђа коначну одлуку. Размотрите слику испод:

Примене случајне шуме
Постоје углавном четири сектора у којима се случајна шума углавном користи:
потхинени рам
Предности случајне шуме
- Рандом Форест је способан да обавља и задатке класификације и регресије.
- Способан је да рукује великим скуповима података високе димензионалности.
- Повећава тачност модела и спречава проблем претеривања.
Недостаци случајне шуме
- Иако се насумична шума може користити и за задатке класификације и за регресијске задатке, она није погоднија за задатке регресије.
Питхон имплементација алгоритма случајне шуме
Сада ћемо имплементирати стабло алгоритма случајне шуме користећи Питхон. За ово ћемо користити исти скуп података 'усер_дата.цсв', који смо користили у претходним моделима класификације. Користећи исти скуп података, можемо упоредити класификатор случајне шуме са другим моделима класификације као што су Класификатор стабла одлучивања, КНН, СВМ, логистичка регресија итд.
Кораци имплементације су дати у наставку:
- Корак претходне обраде података
- Подешавање алгоритма случајне шуме у скуп за обуку
- Предвиђање резултата теста
- Тестирајте тачност резултата (матрица стварања конфузије)
- Визуелизација резултата тестног скупа.
1. Корак претходне обраде података:
Испод је код за корак пре обраде:
# importing libraries import numpy as nm import matplotlib.pyplot as mtp import pandas as pd #importing datasets data_set= pd.read_csv('user_data.csv') #Extracting Independent and dependent Variable x= data_set.iloc[:, [2,3]].values y= data_set.iloc[:, 4].values # Splitting the dataset into training and test set. from sklearn.model_selection import train_test_split x_train, x_test, y_train, y_test= train_test_split(x, y, test_size= 0.25, random_state=0) #feature Scaling from sklearn.preprocessing import StandardScaler st_x= StandardScaler() x_train= st_x.fit_transform(x_train) x_test= st_x.transform(x_test)
У горњем коду смо претходно обрадили податке. Где смо учитали скуп података, који је дат као:

2. Подешавање алгоритма Рандом Форест у сет за обуку:
Сада ћемо алгоритам случајне шуме уклопити у скуп за обуку. Да бисмо га уклопили, увешћемо РандомФорестЦлассифиер разред из склеарн.енсембле библиотека. Код је дат у наставку:
#Fitting Decision Tree classifier to the training set from sklearn.ensemble import RandomForestClassifier classifier= RandomForestClassifier(n_estimators= 10, criterion='entropy') classifier.fit(x_train, y_train)
У горњем коду, објекат класификатора узима следеће параметре:
Излаз:
RandomForestClassifier(bootstrap=True, class_weight=None, criterion='entropy', max_depth=None, max_features='auto', max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, min_samples_leaf=1, min_samples_split=2, min_weight_fraction_leaf=0.0, n_estimators=10, n_jobs=None, oob_score=False, random_state=None, verbose=0, warm_start=False)
3. Предвиђање резултата тестног скупа
Пошто је наш модел уклопљен у сет за обуку, сада можемо предвидети резултат теста. За предвиђање, креираћемо нови вектор предвиђања и_пред. Испод је код за то:
#Predicting the test set result y_pred= classifier.predict(x_test)
Излаз:
Вектор предвиђања је дат као:
нередовно обилажење бинарног стабла

Провером горњег вектора предвиђања и реалног вектора скупа тестова можемо утврдити нетачна предвиђања које је извршио класификатор.
4. Креирање матрице конфузије
Сада ћемо креирати матрицу конфузије да бисмо одредили тачна и нетачна предвиђања. Испод је код за то:
#Creating the Confusion matrix from sklearn.metrics import confusion_matrix cm= confusion_matrix(y_test, y_pred)
Излаз:

Као што видимо у горњој матрици, постоје 4+4= 8 нетачних предвиђања и 64+28= 92 тачна предвиђања.
5. Визуелизација резултата тренинга Сет
Овде ћемо визуелизовати резултат скупа за обуку. Да бисмо визуелизовали резултат скупа за обуку, нацртаћемо график за класификатор случајне шуме. Класификатор ће предвидети да или не за кориснике који су купили или нису купили СУВ аутомобил као што смо то урадили у Логистичкој регресији. Испод је код за то:
израз регресије у Јави
from matplotlib.colors import ListedColormap x_set, y_set = x_train, y_train x1, x2 = nm.meshgrid(nm.arange(start = x_set[:, 0].min() - 1, stop = x_set[:, 0].max() + 1, step =0.01), nm.arange(start = x_set[:, 1].min() - 1, stop = x_set[:, 1].max() + 1, step = 0.01)) mtp.contourf(x1, x2, classifier.predict(nm.array([x1.ravel(), x2.ravel()]).T).reshape(x1.shape), alpha = 0.75, cmap = ListedColormap(('purple','green' ))) mtp.xlim(x1.min(), x1.max()) mtp.ylim(x2.min(), x2.max()) for i, j in enumerate(nm.unique(y_set)): mtp.scatter(x_set[y_set == j, 0], x_set[y_set == j, 1], c = ListedColormap(('purple', 'green'))(i), label = j) mtp.title('Random Forest Algorithm (Training set)') mtp.xlabel('Age') mtp.ylabel('Estimated Salary') mtp.legend() mtp.show()
Излаз:

Горња слика је резултат визуелизације за класификатор Рандом Форест који ради са резултатом скупа за обуку. Веома је сличан класификатору стабла одлука. Свака тачка података одговара сваком кориснику усер_дата, а љубичасти и зелени региони су региони предвиђања. Љубичасти регион је класификован за кориснике који нису купили СУВ аутомобил, а зелени за кориснике који су купили СУВ.
Дакле, у класификатору случајне шуме, узели смо 10 стабала која су предвидела Да или НЕ за променљиву Купљено. Класификатор је узео већину предвиђања и обезбедио резултат.
6. Визуелизација резултата тестног скупа
Сада ћемо визуализовати резултат тестног скупа. Испод је код за то:
#Visulaizing the test set result from matplotlib.colors import ListedColormap x_set, y_set = x_test, y_test x1, x2 = nm.meshgrid(nm.arange(start = x_set[:, 0].min() - 1, stop = x_set[:, 0].max() + 1, step =0.01), nm.arange(start = x_set[:, 1].min() - 1, stop = x_set[:, 1].max() + 1, step = 0.01)) mtp.contourf(x1, x2, classifier.predict(nm.array([x1.ravel(), x2.ravel()]).T).reshape(x1.shape), alpha = 0.75, cmap = ListedColormap(('purple','green' ))) mtp.xlim(x1.min(), x1.max()) mtp.ylim(x2.min(), x2.max()) for i, j in enumerate(nm.unique(y_set)): mtp.scatter(x_set[y_set == j, 0], x_set[y_set == j, 1], c = ListedColormap(('purple', 'green'))(i), label = j) mtp.title('Random Forest Algorithm(Test set)') mtp.xlabel('Age') mtp.ylabel('Estimated Salary') mtp.legend() mtp.show()
Излаз:

Горња слика је резултат визуелизације за скуп тестова. Можемо да проверимо да ли постоји минималан број нетачних предвиђања (8) без проблема са преоптерећењем. Променом броја стабала у класификатору добићемо различите резултате.
