• Пусхдовн аутомати су начин да се имплементира ЦФГ на исти начин на који дизајнирамо ДФА за редовну граматику. ДФА може запамтити коначну количину информација, али ПДА може запамтити бесконачну количину информација.
• Пусхдовн аутомати су једноставно НФА проширен са 'екстерном стек меморијом'. Додавање стека се користи да би се Пусхдовн аутоматима обезбедила могућност управљања меморијом последњи ушао први. Пусхдовн аутомати могу да чувају неограничену количину информација на стеку. Може приступити ограниченој количини информација на стеку. ПДА може да гурне елемент на врх стека и искочи елемент са врха стека. Да бисте прочитали елемент у стеку, горњи елементи морају бити искочени и изгубљени.
• ПДА је моћнији од ФА. Било који језик који може бити прихватљив од стране ФА може бити прихватљив и за ПДА. ПДА такође прихвата класу језика коју чак ни ФА не може прихватити. Стога је ПДА много супериорнији од ФА.

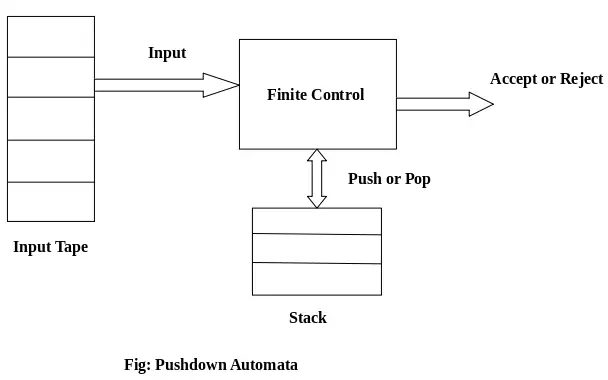
ПДА компоненте:

Улазна трака: Улазна трака је подељена на много ћелија или симбола. Улазна глава је само за читање и може се померати само с лева на десно, један по један симбол.

Коначна контрола: Коначна контрола има неки показивач који показује тренутни симбол који треба прочитати.

Гомила: Гомила је структура у којој можемо гурнути и уклонити ставке само са једног краја. Има бесконачну величину. У ПДА, стек се користи за привремено складиштење ставки.

Формална дефиниција ПДА:

ПДА се може дефинисати као колекција од 7 компоненти:

П: коначни скуп стања

∑: улазни скуп

Ц: симбол стека који се може гурнути и искочити из стека

к0: почетно стање

како проверити величину екрана монитора

СА: почетни симбол који је у Γ.

Ф: скуп коначних стања

д: функција мапирања која се користи за прелазак из тренутног стања у следеће стање.

Тренутни опис (ИД)

ИД је неформална нотација о томе како ПДА израчунава улазни низ и доноси одлуку да ли ће стринг бити прихваћен или одбијен.

Тренутни опис је тројка (к, в, α) где је:

к описује тренутно стање.

Ин описује преостали унос.

својства киселина у дбмс

а описује садржај стека, горе лево.

Ознака окретнице:

Знак ⊢ описује нотацију окретнице и представља један потез.

Знак ⊢* описује низ потеза.

На пример,

(п, б, Т) ⊢ (к, в, α)

римски бројеви графикон 1100

У горњем примеру, док се врши прелаз из стања п у к, улазни симбол 'б' се троши, а врх стека 'Т' је представљен новим стрингом α.

Пример 1:

Дизајнирајте ПДА за прихватање језика а^нб^2н.

Решење: У овом језику, н броја а треба да буде праћено 2н бројем б. Дакле, применићемо врло једноставну логику, а то је ако читамо једно 'а', убацићемо два а на стек. Чим прочитамо 'б' онда за свако појединачно 'б' само једно 'а' треба да буде искочило из стека.

ИД се може конструисати на следећи начин:

 δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) 

Сада када прочитамо б, променићемо стање из к0 у к1 и почети да искаче одговарајуће 'а'. Стога,

 δ(q0, b, a) = (q1, ε) 

Стога ће се овај процес искакања 'б' поновити осим ако се не прочитају сви симболи. Имајте на уму да се акција искакања дешава само у стању к1.

 δ(q1, b, a) = (q1, ε) 

Након читања свих б, сва одговарајућа а би требало да се искоче. Дакле, када читамо ε као улазни симбол онда у стеку не би требало бити ништа. Дакле, потез ће бити:

 δ(q1, ε, Z) = (q2, ε) 

Где

ПДА = ({к0, к1, к2}, {а, б}, {а, З}, δ, к0, З, {к2})

ИД можемо резимирати као:

 δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) δ(q0, b, a) = (q1, ε) δ(q1, b, a) = (q1, ε) δ(q1, ε, Z) = (q2, ε) 

Сада ћемо симулирати овај ПДА за улазни низ 'ааабббббб'.

 δ(q0, aaabbbbbb, Z) ⊢ δ(q0, aabbbbbb, aaZ) ⊢ δ(q0, abbbbbb, aaaaZ) ⊢ δ(q0, bbbbbb, aaaaaaZ) ⊢ δ(q1, bbbbb, aaaaaZ) ⊢ δ(q1, bbbb, aaaaZ) ⊢ δ(q1, bbb, aaaZ) ⊢ δ(q1, bb, aaZ) ⊢ δ(q1, b, aZ) ⊢ δ(q1, ε, Z) ⊢ δ(q2, ε) ACCEPT 

Пример 2:

Дизајнирајте ПДА за прихватање језика 0^н1^м0^н.

Решење: У овом ПДА-у, након н броја 0 следи било који број 1 иза којих следи н броја 0. Стога ће логика дизајна таквог ПДА бити следећа:

Гурните све 0 на стек када наиђете на прве 0. Онда, ако прочитамо 1, само не чинимо ништа. Затим прочитајте 0, и на сваком читању од 0, избаците једну 0 из стека.

индекоф јава

На пример:

Овај сценарио се може написати у ИД обрасцу као:

 δ(q0, 0, Z) = δ(q0, 0Z) δ(q0, 0, 0) = δ(q0, 00) δ(q0, 1, 0) = δ(q1, 0) δ(q0, 1, 0) = δ(q1, 0) δ(q1, 0, 0) = δ(q1, ε) δ(q0, ε, Z) = δ(q2, Z) (ACCEPT state) 

Сада ћемо симулирати овај ПДА за улазни низ '0011100'.

 δ(q0, 0011100, Z) ⊢ δ(q0, 011100, 0Z) ⊢ δ(q0, 11100, 00Z) ⊢ δ(q0, 1100, 00Z) ⊢ δ(q1, 100, 00Z) ⊢ δ(q1, 00, 00Z) ⊢ δ(q1, 0, 0Z) ⊢ δ(q1, ε, Z) ⊢ δ(q2, Z) ACCEPT