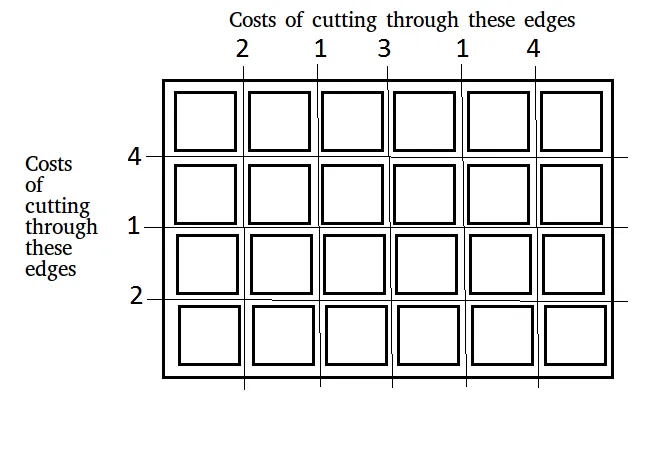
С обзиром на таблу димензија н × м које треба исећи на н × м квадрата. Трошкови реза дуж хоризонталне или вертикалне ивице су дати у два низа:

• к[] : Трошкови сечења дуж вертикалних ивица (по дужини).
• и [] : Трошкови сечења дуж хоризонталних ивица (по ширини).

Пронађите минимални укупни трошак потребан за оптимално сечење плоче на квадрате.

Примери: 

Улаз: к[] = [2 1 3 1 4] и[] = [4 1 2] н = 4 м = 6
Излаз: 42
Објашњење:

У почетку бр. хоризонталних сегмената = 1 & бр. вертикалних сегмената = 1.
Оптималан начин резања на квадрат је:
Изаберите 4 (од к) -> вертикални рез Цена = 4 × хоризонтални сегменти = 4
 Сада хоризонтални сегменти = 1 вертикални сегменти = 2.
Изаберите 4 (од и) -> хоризонтални рез Цена = 4 × вертикални сегменти = 8
 Сада хоризонтални сегменти = 2 вертикална сегмента = 2.
Изаберите 3 (од к) -> вертикални рез Цена = 3 × хоризонтални сегменти = 6
 Сада хоризонтални сегменти = 2 вертикална сегмента = 3.
Изаберите 2 (од к) -> вертикални рез Цена = 2 × хоризонтални сегменти = 4
 Сада хоризонтални сегменти = 2 вертикална сегмента = 4.
Изаберите 2 (од и) -> хоризонтални рез Цена = 2 × вертикални сегменти = 8
 Сада хоризонтални сегменти = 3 вертикална сегмента = 4.
Изаберите 1 (од к) -> вертикални рез Цена = 1 × хоризонтални сегменти = 3
Сада хоризонтални сегменти = 3 вертикална сегмента = 5.
Изаберите 1 (од к) -> вертикални рез Цена = 1 × хоризонтални сегменти = 3
Сада хоризонтални сегменти = 3 вертикална сегмента = 6.
Изаберите 1 (од и) -> хоризонтални рез Цена = 1 × вертикални сегменти = 6
Сада хоризонтални сегменти = 4 вертикална сегмента = 6.
Дакле, укупни трошак = 4 + 8 + 6 + 4 + 8 + 3 + 3 + 6 = 42.

Улаз: к[] = [1 1 1] и[] = [1 1 1] н = 4 м = 4
Излаз: 15
Објашњење:
У почетку бр. хоризонталних сегмената = 1 & бр. вертикалних сегмената = 1.
Оптималан начин резања на квадрат је:
Изаберите 1 (од и) -> хоризонтални рез Цена = 1 × вертикални сегменти = 1
Сада хоризонтални сегменти = 2 вертикална сегмента = 1.
Изаберите 1 (од и) -> хоризонтални рез Цена = 1 × вертикални сегменти = 1
Сада хоризонтални сегменти = 3 вертикална сегмента = 1.
Изаберите 1 (од и) -> хоризонтални рез Цена = 1 × вертикални сегменти = 1
Сада хоризонтални сегменти = 4 вертикална сегмента = 1.
Изаберите 1 (од к) -> вертикални рез Цена = 1 × хоризонтални сегменти = 4
Сада хоризонтални сегменти = 4 вертикална сегмента = 2.
Изаберите 1 (од к) -> вертикални рез Цена = 1 × хоризонтални сегменти = 4
Сада хоризонтални сегменти = 4 вертикална сегмента = 3.
Изаберите 1 (од к) -> вертикални рез Цена = 1 × хоризонтални сегменти = 4
Сада хоризонтални сегменти = 4 вертикална сегмента = 4
Дакле, укупни трошак = 1 + 1 + 1 + 4 + 4 + 4 = 15.

Садржај

• [Наивни приступ] Пробајте све пермутације - О((н+м)!×(н+м)) Време и О(н+м) простор
• [Очекивани приступ] Коришћење похлепне технике - О( н (лог н)+м (лог м)) Време и О(1) простор

[Наивни приступ] Пробајте све пермутације - О((н+м)!×(н+м)) Време и О(н+м) простор

Идеја је да се генеришу све могуће пермутације датих резова и затим израчунају трошкови за сваку пермутацију. Коначно вратите минимални трошак међу њима.

Напомена: Овај приступ није изводљив за веће инпуте јер број пермутација расте факторски као (м+н-2)!.
За сваку пермутацију морамо израчунати цену у О(м+н) времену. Отуда укупна временска сложеност постаје О((м+н−2)!×(м+н)).

[Очекивани приступ] Коришћење похлепне технике - О( н (лог н)+м (лог м)) Време и О(1) простор

Идеја је да се прво направе најскупљи резови користећи а похлепан приступ . Запажање је да одабир највећег смањења трошкова у сваком кораку смањује будуће трошкове тако што утиче на више комада одједном. Ми сортирамо вертикално (к) и хоризонтално (и) смањење трошкова у опадајућем редоследу, а затим итеративно бирамо већи да бисмо максимизирали уштеде. Преостали резови се обрађују одвојено како би се осигурало да су сви делови оптимално подељени.

Шта се дешава када направимо рез?

• Хоризонтални рез → сечете по ширини тако да се повећава број хоризонталних трака (хЦоунт++). Али цена се множи са вЦоунт (број вертикалних трака) јер хоризонтални рез мора да прође кроз све вертикалне сегменте.
• Вертикални рез → сечете по висини тако да се број вертикалних трака повећава (вЦоунт++). Али цена се множи са хЦоунт (број хоризонталних трака) јер вертикални рез мора да прође кроз све хоризонталне сегменте.

Кораци за решавање проблема:

• Сортирајте и к и и низови у опадајућем редоследу.
• Користите два показивача, један за к и један за и почевши од највеће вредности и померајући се ка мањим вредностима.
• Одржавајте хЦоунт и вЦоунт да бисте пратили на колико сегмената утиче сваки рез и ажурирајте их у складу са тим.
• Итерирајте док и к и  и имају необрађене резове и увек бирате већи трошак да бисте минимизирали укупне трошкове.
• Ако к има преостале резове, обрадите их множитељем хЦоунт; на сличан начин обрадите преостале и резове помоћу вЦоунт.
• Акумулирајте укупне трошкове у сваком кораку користећи формулу: смањите цену * број погођених делова да бисте обезбедили минималне трошкове.

#include   #include #include   using namespace std; int minCost(int n int m   vector<int>& x vector<int>& y) {    // Sort the cutting costs in ascending order  sort(x.begin() x.end());  sort(y.begin() y.end());   int hCount = 1 vCount = 1;   int i = x.size() - 1 j = y.size() - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } int main() {    int n = 4 m = 6;  vector<int> x = {2 1 3 1 4};  vector<int> y = {4 1 2};  cout << minCost(n m x y) << endl;  return 0; } 

import java.util.Arrays; class GfG {    static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Arrays.sort(x);  Arrays.sort(y);   int hCount = 1 vCount = 1;   int i = x.length - 1 j = y.length - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }  public static void main(String[] args) {    int n = 4m = 6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  System.out.println(minCost(n m x y));  } } 

def minCost(nm x y): # Sort the cutting costs in ascending order x.sort() y.sort() hCount vCount = 1 1 i j = len(x) - 1 len(y) - 1 totalCost = 0 while i >= 0 and j >= 0: # Choose the larger cost cut to  # minimize future costs if x[i] >= y[j]: totalCost += x[i] * hCount vCount += 1 i -= 1 else: totalCost += y[j] * vCount hCount += 1 j -= 1 # Process remaining vertical cuts while i >= 0: totalCost += x[i] * hCount vCount += 1 i -= 1 # Process remaining horizontal cuts while j >= 0: totalCost += y[j] * vCount hCount += 1 j -= 1 return totalCost if __name__ == '__main__': nm = 4 6 x = [2 1 3 1 4] y = [4 1 2] print(minCost(nmx y)) 

using System; class GfG {  public static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Array.Sort(x);  Array.Sort(y);  int hCount = 1 vCount = 1;  int i = x.Length - 1 j = y.Length - 1;  int totalCost = 0;  // Process the cuts in greedy manner  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }    public static void Main() {    int n=4m=6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  Console.WriteLine(minCost(nm x y));  } } 

function minCost( nm x y) {    // Sort the cutting costs in ascending order  x.sort((a b) => a - b);  y.sort((a b) => a - b);  let hCount = 1 vCount = 1;  let i = x.length - 1 j = y.length - 1;  let totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }   else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } // Driver Code let n = 4m = 6; let x = [2 1 3 1 4]; let y = [4 1 2]; console.log(minCost(nm x y)); 

42