- Проучавали смо стратегије које могу да размишљају унапред или уназад, али мешавина два правца је прикладна за решавање сложеног и великог проблема. Оваква мешовита стратегија омогућава да се прво реши већи део проблема, а затим се врати и реши мали проблеми који настану комбиновањем великих делова проблема. Таква техника се зове Анализа средстава и циљева .
- Анализа средстава и циљева је техника решавања проблема која се користи у вештачкој интелигенцији за ограничавање претраге у АИ програмима.
- То је мешавина технике претраживања уназад и унапред.
- МЕА технику су први увели 1961. године Ален Њуел и Херберт А. Сајмон у свом компјутерском програму за решавање проблема, који је назван Генерал Проблем Солвер (ГПС).
- Процес анализе МЕА био је усредсређен на процену разлике између тренутног и циљног стања.
Како функционише анализа средстава и циља:
Процес анализе средстава и циљева може се рекурзивно применити на проблем. То је стратегија за контролу претраге у решавању проблема. Следе главни кораци који описују рад МЕА технике за решавање проблема.
- Прво, процените разлику између почетног и коначног стања.
- Изаберите различите операторе који се могу применити за сваку разлику.
- Примените оператор на сваку разлику, чиме се смањује разлика између тренутног стања и циљног стања.
Подциљање оператера
У МЕА процесу откривамо разлике између тренутног стања и циљног стања. Када дође до ових разлика, можемо применити оператор да смањимо разлике. Али понекад је могуће да се оператор не може применити на тренутно стање. Тако креирамо подпроблем тренутног стања, у којем се оператор може применити, такав тип уланчавања уназад у коме се бирају оператори, а затим постављају подциљеви да би се успоставили предуслови оператора назива се Подциљање оператера .
Алгоритам за анализу средстава и циљева:
Узмимо тренутно стање као ТРЕНУТНО и стање циља као ЦИЉ, а затим следе кораци за МЕА алгоритам.
- Изаберите нови оператор О који је применљив за тренутну разлику, а ако нема тог оператора, сигнализирајте неуспех.
- Покушај примене оператора О на ЦУРРЕНТ. Направите опис два стања.
и) О-Старт, стање у којем су испуњени предуслови О.
ии) О-Резултат, стање које би резултирало ако се О примени у О-старт. - Ако
(Први део<------ mea (current, o-start)< strong>
И
(Задњи део<----- mea (o-result, goal)< strong>, су успешни, а затим сигнализирају успех и враћају резултат комбиновања ПРВОГ ДЕЛА, О и ПОСЛЕДЊЕГ ДЕЛА.
Горе описани алгоритам је погоднији за једноставан проблем, а не адекватан за решавање сложених проблема.
Пример анализе средње вредности:
Узмимо пример где знамо почетно стање и циљно стање као што је дато у наставку. У овом задатку, потребно је да добијемо циљно стање проналажењем разлика између почетног стања и циљног стања и применом оператора.
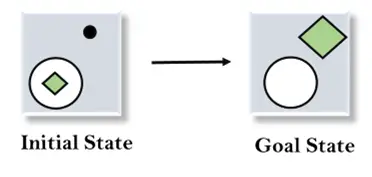
Решење:
Да бисмо решили горњи проблем, прво ћемо пронаћи разлике између почетних стања и циљних стања, а за сваку разлику ћемо генерисати ново стање и применити операторе. Оператери које имамо за овај проблем су:
веза јава мискл
1. Процена почетног стања: У првом кораку ћемо проценити почетно стање и упоредићемо почетно и циљно стање да бисмо пронашли разлике између оба стања.

2. Примена оператора Делете: Као што можемо да проверимо, прва разлика је у томе што у стању циља не постоји симбол тачке који је присутан у почетном стању, па ћемо прво применити Избриши оператор да бисте уклонили ову тачку.

3. Примена оператора премештања: Након примене оператора Делете, долази до новог стања које ћемо поново упоредити са стањем циља. Након поређења ових стања, постоји још једна разлика у томе што је квадрат изван круга, па ћемо применити Оператор померања .

4. Примена оператора проширења: Сада се у трећем кораку генерише ново стање и ми ћемо упоредити ово стање са стањем циља. Након поређења стања још увек постоји једна разлика, а то је величина квадрата, па ћемо применити Оператор проширења , и коначно, генерише циљно стање.

