С обзиром на низ н елемената и два цела броја а б који припадају датом низу. Направите а Бинарно стабло претраге уметањем елемената из арр[0] до арр[н-1] . Задатак је пронаћи максимум елемент на путу од а до б.
Пример:
Улаз: арр[] = { 18 36 9 6 12 10 1 8 } а = 1 б = 10.
Излаз : 12
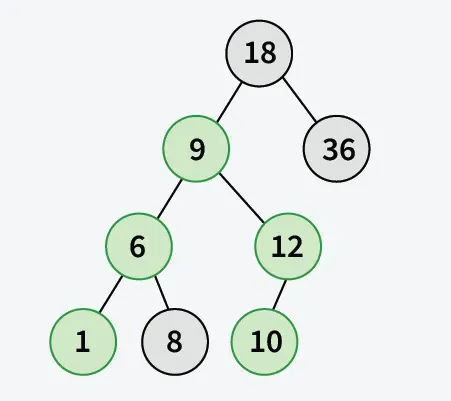
Објашњење: Пут од 1 до 10 садржи { 1 6 9 12 10 } . Максимални елемент је 12.
Садржај
- [Наивни приступ] Коришћење хеширања - О(н * лог н) Време и О(н) Простор
- [Очекивани приступ] Коришћење ЛЦА два чвора - О(х) Време и О(х) Простор
[Наивни приступ] Коришћење хеширања - О(н * лог н) Време и О(н) Простор
Идеја је да се користи а хасхмап за чување родитељ чвор сваког чвора у бинарно стабло претраге . Можемо почети од оба дата чвора и прећи стаблом чувајући чворове на које се наилази у а сет . Једном када дођемо до корена или заједничког претка два чвора, можемо прећи низ дрво од сваког чвора и пронаћи максимум елемент који се среће у скупу чворова.
како одредити величину монитора
Кораци алгоритма за горњи приступ:
- Направите празно хасх табле за чување родитељ чвор сваког чвора у бинарном стаблу претраге.
- Извршите а претрага у дубину (ДФС) обилазак бинарног стабла претраге и попунити хеш табелу са родитељским чвором сваког чвора.
- Иницијализујте два показивача рецимо п1 и п2 на дате чворове.
- Иницијализујте два празна скупа рецимо с1 и с2 за чување чворова на које наиђете док се крећете по стаблу од п1 и п2 односно.
- Док п1 и п2 су није једнака урадите следеће:
- Ако п1 није нулл додајте га у скуп с1 и ажурирати п1 свом родитељском чвору користећи хеш табелу.
- Ако п2 није нулл додајте га у скуп с2 и ажурирати п2 свом родитељском чвору користећи хеш табелу.
- Пронађите скуп пресека од с1 и с2 односно скуп чворова који су заједнички и за с1 и за с2.
- На овој раскрсници пронађите максимум елемент и врати га.
Испод је примена горњег приступа:
C++// C++ program to find maximum element in the path // between two Nodes of Binary Search Tree. #include
// Java program to find the maximum element in the path // between two Nodes of Binary Search Tree. import java.util.*; class Node { int data; Node left right; Node(int x) { data = x; left = right = null; } } class GfG { // Insert a new Node in Binary Search Tree static void insertNode(Node root int x) { Node current = root parent = null; // Traverse to the correct position // for insertion while (current != null) { parent = current; if (x < current.data) current = current.left; else current = current.right; } // Insert new Node at the correct position if (parent == null) root = new Node(x); else if (x < parent.data) parent.left = new Node(x); else parent.right = new Node(x); } // DFS to populate parent map for each node static void dfs(Node root Map<Node Node> parentMap Node parent) { if (root == null) return; // Store the parent of the current node if (parent != null) { parentMap.put(root parent); } // Recur for left and right children dfs(root.left parentMap root); dfs(root.right parentMap root); } // Function to find the node with the given // value in the BST static Node findNode(Node root int val) { if (root == null) return null; if (root.data == val) return root; Node leftResult = findNode(root.left val); if (leftResult != null) return leftResult; return findNode(root.right val); } // Find maximum element in the path between // two nodes in BST static int findMaxElement(Node root int x int y) { Map<Node Node> parentMap = new HashMap<>(); // Populate parent map with DFS dfs(root parentMap null); // Find the nodes corresponding to // the values x and y Node p1 = findNode(root x); Node p2 = findNode(root y); // If nodes not found if (p1 == null || p2 == null) return -1; // Sets to store nodes encountered // while traversing up the tree Set<Node> s1 = new HashSet<>(); Set<Node> s2 = new HashSet<>(); // Variable to store the maximum element // in the path int maxElement = Integer.MIN_VALUE; // Traverse up the tree from p1 and p2 // and add nodes to sets s1 and s2 while (p1 != p2) { if (p1 != null) { s1.add(p1); maxElement = Math.max(maxElement p1.data); // Move to parent node p1 = parentMap.get(p1); } if (p2 != null) { s2.add(p2); maxElement = Math.max(maxElement p2.data); p2 = parentMap.get(p2); } // Check if there's a common node in both sets if (s1.contains(p2)) break; if (s2.contains(p1)) break; } // Now both p1 and p2 point to their // Lowest Common Ancestor (LCA) maxElement = Math.max(maxElement p1.data); return maxElement; } public static void main(String[] args) { int[] arr = {18 36 9 6 12 10 1 8}; int a = 1 b = 10; int n = arr.length; Node root = new Node(arr[0]); for (int i = 1; i < n; i++) insertNode(root arr[i]); System.out.println(findMaxElement(root a b)); } }
# Python program to find maximum element in the path # between two Nodes of Binary Search Tree. class Node: def __init__(self x): self.data = x self.left = None self.right = None # Insert a new Node in Binary Search Tree def insert_node(root x): current = root parent = None # Traverse to the correct position for insertion while current is not None: parent = current if x < current.data: current = current.left else: current = current.right # Insert new Node at the correct position if parent is None: root = Node(x) elif x < parent.data: parent.left = Node(x) else: parent.right = Node(x) # DFS to populate parent map for each node def dfs(root parent_map parent=None): if root is None: return # Store the parent of the current node if parent is not None: parent_map[root] = parent # Recur for left and right children dfs(root.left parent_map root) dfs(root.right parent_map root) # Function to find the node with the given # value in the BST def find_node(root val): if root is None: return None if root.data == val: return root left_result = find_node(root.left val) if left_result: return left_result return find_node(root.right val) # Find maximum element in the path between # two nodes in BST def find_max_element(root x y): parent_map = {} # Populate parent map with DFS dfs(root parent_map) # Find the nodes corresponding to the # values x and y p1 = find_node(root x) p2 = find_node(root y) # If nodes not found if not p1 or not p2: return -1 # Sets to store nodes encountered # while traversing up the tree s1 = set() s2 = set() # Variable to store the maximum element in the path max_element = float('-inf') # Traverse up the tree from p1 and p2 # and add nodes to sets s1 and s2 while p1 != p2: if p1: s1.add(p1) max_element = max(max_element p1.data) # Move to parent node p1 = parent_map.get(p1) if p2: s2.add(p2) max_element = max(max_element p2.data) p2 = parent_map.get(p2) # Check if there's a common node in both sets if p2 in s1: break if p1 in s2: break # Now both p1 and p2 point to their # Lowest Common Ancestor (LCA) max_element = max(max_element p1.data) return max_element if __name__ == '__main__': arr = [18 36 9 6 12 10 1 8] a b = 1 10 n = len(arr) root = Node(arr[0]) for i in range(1 n): insert_node(root arr[i]) print(find_max_element(root a b))
// C# program to find the maximum element in the path // between two Nodes of Binary Search Tree. using System; using System.Collections.Generic; class Node { public int data; public Node left right; public Node(int x) { data = x; left = right = null; } } class GfG { // Insert a new Node in Binary Search Tree static public void insertNode(Node root int x) { Node current = root parent = null; // Traverse to the correct position // for insertion while (current != null) { parent = current; if (x < current.data) current = current.left; else current = current.right; } // Insert new Node at the correct // position if (parent == null) root = new Node(x); else if (x < parent.data) parent.left = new Node(x); else parent.right = new Node(x); } // DFS to populate parent map for each node static public void dfs(Node root Dictionary<Node Node> parentMap Node parent) { if (root == null) return; // Store the parent of the current node if (parent != null) { parentMap[root] = parent; } // Recur for left and right children dfs(root.left parentMap root); dfs(root.right parentMap root); } // Function to find the node with the given // value in the BST static public Node findNode(Node root int val) { if (root == null) return null; if (root.data == val) return root; Node leftResult = findNode(root.left val); if (leftResult != null) return leftResult; return findNode(root.right val); } // Find maximum element in the path between // two nodes in BST static public int findMaxElement(Node root int x int y) { Dictionary<Node Node> parentMap = new Dictionary<Node Node>(); // Populate parent map with DFS dfs(root parentMap null); // Find the nodes corresponding to // the values x and y Node p1 = findNode(root x); Node p2 = findNode(root y); // If nodes not found if (p1 == null || p2 == null) return -1; // Sets to store nodes encountered // while traversing up the tree HashSet<Node> s1 = new HashSet<Node>(); HashSet<Node> s2 = new HashSet<Node>(); // Variable to store the maximum element // in the path int maxElement = int.MinValue; // Traverse up the tree from p1 and p2 // and add nodes to sets s1 and s2 while (p1 != p2) { if (p1 != null) { s1.Add(p1); maxElement = Math.Max(maxElement p1.data); // Move to parent node p1 = parentMap[p1]; } if (p2 != null) { s2.Add(p2); maxElement = Math.Max(maxElement p2.data); p2 = parentMap[p2]; } // Check if there's a common node in both sets if (s1.Contains(p2)) break; if (s2.Contains(p1)) break; } // Now both p1 and p2 point to their Lowest // Common Ancestor (LCA) maxElement = Math.Max(maxElement p1.data); return maxElement; } static void Main() { int[] arr = {18 36 9 6 12 10 1 8}; int a = 1 b = 10; int n = arr.Length; Node root = new Node(arr[0]); for (int i = 1; i < n; i++) insertNode(root arr[i]); Console.WriteLine(findMaxElement(root a b)); } }
// JavaScript program to find the maximum element in the path // between two Nodes of Binary Search Tree. class Node { constructor(x) { this.data = x; this.left = this.right = null; } } // Insert a new Node in Binary Search Tree function insertNode(root x) { let current = root parent = null; // Traverse to the correct position for insertion while (current !== null) { parent = current; if (x < current.data) current = current.left; else current = current.right; } // Insert new Node at the correct position if (parent === null) root = new Node(x); else if (x < parent.data) parent.left = new Node(x); else parent.right = new Node(x); } // DFS to populate parent map for each node function dfs(root parentMap parent = null) { if (root === null) return; // Store the parent of the current node if (parent !== null) { parentMap.set(root parent); } // Recur for left and right children dfs(root.left parentMap root); dfs(root.right parentMap root); } // Function to find the node with the given // value in the BST function findNode(root val) { if (root === null) return null; if (root.data === val) return root; let leftResult = findNode(root.left val); if (leftResult !== null) return leftResult; return findNode(root.right val); } // Find maximum element in the path // between two nodes in BST function findMaxElement(root x y) { let parentMap = new Map(); // Populate parent map with DFS dfs(root parentMap); // Find the nodes corresponding to the // values x and y let p1 = findNode(root x); let p2 = findNode(root y); // If nodes not found if (p1 === null || p2 === null) return -1; // Sets to store nodes encountered let s1 = new Set(); let s2 = new Set(); // Variable to store the maximum // element in the path let maxElement = -Infinity; // Traverse up the tree from p1 and p2 // and add nodes to sets s1 and s2 while (p1 !== p2) { if (p1 !== null) { s1.add(p1); maxElement = Math.max(maxElement p1.data); // Move to parent node p1 = parentMap.get(p1); } if (p2 !== null) { s2.add(p2); maxElement = Math.max(maxElement p2.data); p2 = parentMap.get(p2); } // Check if there's a common node in both sets if (s1.has(p2)) break; if (s2.has(p1)) break; } // Now both p1 and p2 point to their Lowest // Common Ancestor (LCA) maxElement = Math.max(maxElement p1.data); return maxElement; } let arr = [18 36 9 6 12 10 1 8]; let a = 1 b = 10; let n = arr.length; let root = new Node(arr[0]); for (let i = 1; i < n; i++) insertNode(root arr[i]); console.log(findMaxElement(root a b));
Излаз
12
[Очекивани приступ] Коришћење ЛЦА два чвора - О(х) Време и О(х) Простор
Идеја је пронаћи Најнижи заједнички предак чвора 'а' и чвора 'б'. Затим потражите максимални чвор између ЛЦА и 'а' и такође пронађите максимални чвор између ЛЦА и 'б'. Одговор ће бити максимални чвор од два.
Испод је имплементација горњег алгоритма:
C++// C++ program to find maximum element in the path // between two Nodes of Binary Search Tree. #include
// Java program to find maximum element in the path // between two Nodes of Binary Search Tree. import java.util.*; class Node { int data; Node left right; Node(int x) { data = x; left = right = null; } } class GfG { // Insert a new Node in Binary Search Tree static void insertNode(Node root int x) { Node current = root parent = null; // Traverse to the correct // position for insertion while (current != null) { parent = current; if (x < current.data) current = current.left; else current = current.right; } // Insert new Node at the correct // position if (parent == null) root = new Node(x); else if (x < parent.data) parent.left = new Node(x); else parent.right = new Node(x); } // Find maximum element in the path from // an ancestor to a node static int maxInPath(Node root int x) { int maxElement = Integer.MIN_VALUE; Node current = root; // Traverse the path from root to the // target node 'x' while (current != null && current.data != x) { maxElement = Math.max(maxElement current.data); if (x < current.data) current = current.left; else current = current.right; } return Math.max(maxElement x); } // Find maximum element in the path between two // nodes in BST static int findMaxElement(Node root int x int y) { Node current = root; // Find Lowest Common Ancestor (LCA) of x and y while ((x < current.data && y < current.data) || (x > current.data && y > current.data)) { if (x < current.data && y < current.data) current = current.left; else if (x > current.data && y > current.data) current = current.right; } // Find maximum elements in paths from LCA // to x and LCA to y return Math.max(maxInPath(current x) maxInPath(current y)); } public static void main(String[] args) { int[] arr = {18 36 9 6 12 10 1 8}; int a = 1 b = 10; Node root = new Node(arr[0]); for (int i = 1; i < arr.length; i++) insertNode(root arr[i]); System.out.println(findMaxElement(root a b)); } }
# Python program to find maximum element in the path # between two Nodes of Binary Search Tree. class Node: def __init__(self x): self.data = x self.left = None self.right = None # Insert a new Node in Binary Search Tree def insertNode(root x): current = root parent = None # Traverse to the correct position for insertion while current is not None: parent = current if x < current.data: current = current.left else: current = current.right # Insert new Node at the correct position if parent is None: root = Node(x) elif x < parent.data: parent.left = Node(x) else: parent.right = Node(x) # Find maximum element in the path from an # ancestor to a node def maxInPath(root x): maxElement = float('-inf') current = root # Traverse the path from root to the # target node 'x' while current is not None and current.data != x: maxElement = max(maxElement current.data) if x < current.data: current = current.left else: current = current.right return max(maxElement x) # Find maximum element in the path between # two nodes in BST def findMaxElement(root x y): current = root # Find Lowest Common Ancestor (LCA) of x and y while (x < current.data and y < current.data) or (x > current.data and y > current.data): if x < current.data and y < current.data: current = current.left elif x > current.data and y > current.data: current = current.right # Find maximum elements in paths from LCA to # x and LCA to y return max(maxInPath(current x) maxInPath(current y)) if __name__ == '__main__': arr = [18 36 9 6 12 10 1 8] a b = 1 10 root = Node(arr[0]) for i in range(1 len(arr)): insertNode(root arr[i]) print(findMaxElement(root a b))
// C# program to find maximum element in the path // between two Nodes of Binary Search Tree. using System; class Node { public int data; public Node left right; public Node(int x) { data = x; left = right = null; } } class GfG { // Insert a new Node in Binary Search Tree static void insertNode(Node root int x) { Node current = root parent = null; // Traverse to the correct position // for insertion while (current != null) { parent = current; if (x < current.data) current = current.left; else current = current.right; } // Insert new Node at the correct position if (parent == null) root = new Node(x); else if (x < parent.data) parent.left = new Node(x); else parent.right = new Node(x); } // Find maximum element in the path from an // ancestor to a node static int maxInPath(Node root int x) { int maxElement = int.MinValue; Node current = root; // Traverse the path from root to the target node 'x' while (current != null && current.data != x) { maxElement = Math.Max(maxElement current.data); if (x < current.data) current = current.left; else current = current.right; } return Math.Max(maxElement x); } // Find maximum element in the path between two nodes in BST static int findMaxElement(Node root int x int y) { Node current = root; // Find Lowest Common Ancestor (LCA) of x and y while ((x < current.data && y < current.data) || (x > current.data && y > current.data)) { if (x < current.data && y < current.data) current = current.left; else if (x > current.data && y > current.data) current = current.right; } // Find maximum elements in paths from // LCA to x and LCA to y return Math.Max(maxInPath(current x) maxInPath(current y)); } static void Main() { int[] arr = {18 36 9 6 12 10 1 8}; int a = 1 b = 10; Node root = new Node(arr[0]); for (int i = 1; i < arr.Length; i++) insertNode(root arr[i]); Console.WriteLine(findMaxElement(root a b)); } }
// JavaScript program to find maximum element in the path // between two Nodes of Binary Search Tree. class Node { constructor(x) { this.data = x; this.left = null; this.right = null; } } // Insert a new Node in Binary Search Tree function insertNode(root x) { let current = root parent = null; // Traverse to the correct position for insertion while (current !== null) { parent = current; if (x < current.data) current = current.left; else current = current.right; } // Insert new Node at the correct position if (parent === null) root = new Node(x); else if (x < parent.data) parent.left = new Node(x); else parent.right = new Node(x); } // Find maximum element in the path from an // ancestor to a node function maxInPath(root x) { let maxElement = -Infinity; let current = root; // Traverse the path from root to the target node 'x' while (current !== null && current.data !== x) { maxElement = Math.max(maxElement current.data); if (x < current.data) current = current.left; else current = current.right; } return Math.max(maxElement x); } // Find maximum element in the path between // two nodes in BST function findMaxElement(root x y) { let current = root; // Find Lowest Common Ancestor (LCA) of x and y while ((x < current.data && y < current.data) || (x > current.data && y > current.data)) { if (x < current.data && y < current.data) current = current.left; else if (x > current.data && y > current.data) current = current.right; } // Find maximum elements in paths from LCA to // x and LCA to y return Math.max(maxInPath(current x) maxInPath(current y)); } const arr = [18 36 9 6 12 10 1 8]; const a = 1 b = 10; const root = new Node(arr[0]); for (let i = 1; i < arr.length; i++) { insertNode(root arr[i]); } console.log(findMaxElement(root a b));
Излаз
12Креирај квиз

