Шта је Хеап?

Хрпа је потпуно бинарно стабло, а бинарно стабло је дрво у коме чвор може имати највише два детета. Пре него што сазнате више о хрпи Шта је потпуно бинарно стабло?

Потпуно бинарно стабло је а бинарно стабло у коме сви нивои осим последњег нивоа, односно листног чвора треба да буду потпуно попуњени, а сви чворови треба да буду поравнати лево.

Хајде да разумемо кроз пример.

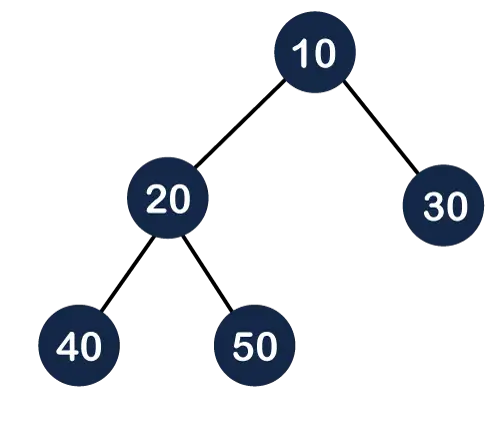
На горњој слици можемо приметити да су сви унутрашњи чворови потпуно попуњени осим лисног чвора; стога можемо рећи да је горе наведено стабло потпуно бинарно стабло.

апликације рачунарства у облаку

Горња слика показује да су сви унутрашњи чворови потпуно попуњени осим лисног чвора, али су листови чворови додати у десном делу; стога, горе наведено стабло није потпуно бинарно стабло.

Напомена: Хеап стабло је посебна структура података избалансираног бинарног стабла где се коренски чвор пореди са својим потомцима и у складу с тим распоређује.

Како можемо уредити чворове у Дрвету?

Постоје две врсте гомиле:

• Мин Хеап
• Мак хеап

Мин хрпа: Вредност родитељског чвора треба да буде мања или једнака било ком од његових потомака.

Ор

Другим речима, мин-хеап се може дефинисати као, за сваки чвор и, вредност чвора и већа или једнака његовој родитељској вредности осим основног чвора. Математички се може дефинисати као:

А[Родитељ(и)]<= a[i]< strong>

Хајде да разумемо мин-хеап кроз пример.

На горњој слици, 11 је основни чвор, а вредност коренског чвора је мања од вредности свих осталих чворова (лево дете или десно дете).

Макс. хрпа: Вредност родитељског чвора је већа или једнака његовим потомцима.

Ор

Другим речима, максимална хрпа се може дефинисати као за сваки чвор и; вредност чвора и је мања или једнака његовој родитељској вредности осим основног чвора. Математички се може дефинисати као:

А[Родитељ(и)] >= А[и]

Горње стабло је максимално стабло гомиле јер задовољава својство максималне гомиле. Сада, да видимо приказ низа максималне гомиле.

Временска сложеност у Мак Хеап-у

Укупан број потребних поређења за максималну хрпу је према висини стабла. Висина комплетног бинарног стабла је увек логн; стога би временска сложеност такође била О(логн).

Алгоритам операције уметања у мак хеап.

 // algorithm to insert an element in the max heap. insertHeap(A, n, value) { n=n+1; // n is incremented to insert the new element A[n]=value; // assign new value at the nth position i = n; // assign the value of n to i // loop will be executed until i becomes 1. while(i&gt;1) { parent= floor value of i/2; // Calculating the floor value of i/2 // Condition to check whether the value of parent is less than the given node or not if(A[parent] <a[i]) { swap(a[parent], a[i]); i="parent;" } else return; < pre> <p> <strong>Let&apos;s understand the max heap through an example</strong> .</p> <p>In the above figure, 55 is the parent node and it is greater than both of its child, and 11 is the parent of 9 and 8, so 11 is also greater than from both of its child. Therefore, we can say that the above tree is a max heap tree.</p> <p> <strong>Insertion in the Heap tree</strong> </p> <p> <strong>44, 33, 77, 11, 55, 88, 66</strong> </p> <p>Suppose we want to create the max heap tree. To create the max heap tree, we need to consider the following two cases:</p> <ul> <li>First, we have to insert the element in such a way that the property of the complete binary tree must be maintained.</li> <li>Secondly, the value of the parent node should be greater than the either of its child.</li> </ul> <p> <strong>Step 1:</strong> First we add the 44 element in the tree as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-5.webp" alt="Heap Data Structure"> <p> <strong>Step 2:</strong> The next element is 33. As we know that insertion in the binary tree always starts from the left side so 44 will be added at the left of 33 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-6.webp" alt="Heap Data Structure"> <p> <strong>Step 3:</strong> The next element is 77 and it will be added to the right of the 44 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-7.webp" alt="Heap Data Structure"> <p>As we can observe in the above tree that it does not satisfy the max heap property, i.e., parent node 44 is less than the child 77. So, we will swap these two values as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-8.webp" alt="Heap Data Structure"> <p> <strong>Step 4:</strong> The next element is 11. The node 11 is added to the left of 33 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-9.webp" alt="Heap Data Structure"> <p> <strong>Step 5:</strong> The next element is 55. To make it a complete binary tree, we will add the node 55 to the right of 33 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-10.webp" alt="Heap Data Structure"> <p>As we can observe in the above figure that it does not satisfy the property of the max heap because 33<55, so we will swap these two values as shown below:< p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-11.webp" alt="Heap Data Structure"> <p> <strong>Step 6:</strong> The next element is 88. The left subtree is completed so we will add 88 to the left of 44 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-12.webp" alt="Heap Data Structure"> <p>As we can observe in the above figure that it does not satisfy the property of the max heap because 44<88, so we will swap these two values as shown below:< p> <p>Again, it is violating the max heap property because 88&gt;77 so we will swap these two values as shown below:</p> <p> <strong>Step 7:</strong> The next element is 66. To make a complete binary tree, we will add the 66 element to the right side of 77 as shown below:</p> <p>In the above figure, we can observe that the tree satisfies the property of max heap; therefore, it is a heap tree.</p> <p> <strong>Deletion in Heap Tree</strong> </p> <p>In Deletion in the heap tree, the root node is always deleted and it is replaced with the last element.</p> <p> <strong>Let&apos;s understand the deletion through an example.</strong> </p> <p> <strong>Step 1</strong> : In the above tree, the first 30 node is deleted from the tree and it is replaced with the 15 element as shown below:</p> <p>Now we will heapify the tree. We will check whether the 15 is greater than either of its child or not. 15 is less than 20 so we will swap these two values as shown below:</p> <p>Again, we will compare 15 with its child. Since 15 is greater than 10 so no swapping will occur.</p> <p> <strong>Algorithm to heapify the tree</strong> </p> <pre> MaxHeapify(A, n, i) { int largest =i; int l= 2i; int r= 2i+1; while(lA[largest]) { largest=l; } while(rA[largest]) { largest=r; } if(largest!=i) { swap(A[largest], A[i]); heapify(A, n, largest); }} </pre> <hr></88,></p></55,></p></a[i])>