• Машина коначног стања се користи за препознавање образаца.
• Коначна аутоматска машина узима низ симбола као улаз и у складу са тим мења његово стање. У улазу, када се пронађе жељени симбол, долази до прелаза.
• Током транзиције, аутомати могу или да пређу у следеће стање или да остану у истом стању.
• ФА има два стања: стање прихватања или стање одбијања. Када је улазни низ успешно обрађен и аутомати дођу у своје коначно стање онда ће прихватити.

Коначни аутомат се састоји од следећег:

П: коначан скуп стања
∑: коначан скуп улазног симбола
к0: почетно стање
Ф: коначно стање
д: Прелазна функција

Прелазна функција се може дефинисати као

 δ: Q x ∑ →Q 

ФА се карактерише на два начина:

1. ДФА (коначни аутомати)
2. НДФА (недетерминистички коначни аутомати)

ДФА

ДФА је скраћеница од Детерминистиц Фините Аутомата. Детерминистички се односи на јединственост израчунавања. У ДФА, улазни знак иде само у једно стање. ДФА не прихвата нулти потез што значи да ДФА не може да промени стање без било каквог улазног карактера.

ДФА има пет скупова {К, ∑, к0, Ф, δ}

Пример

Погледајте пример детерминистичких коначних аутомата:

 Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q3}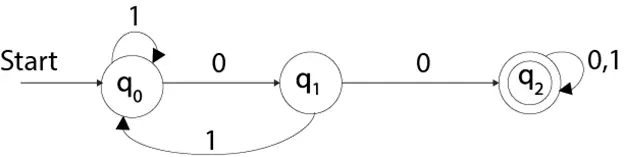 

НДФА

НДФА се односи на недетерминистичке коначне аутомате. Користи се за транзит било којег броја стања за одређени улаз. НДФА прихвата НУЛЛ потез што значи да може да промени стање без читања симбола.

НДФА такође има пет држава истих као и ДФА. Али НДФА има другачију функцију транзиције.

Транзициона функција НДФА се може дефинисати као:

Пример

Погледајте пример недетерминистичких коначних аутомата:

 Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q3}