С обзиром на решетку бројева, пронађите максималну дужину змија и исписати га. Ако вишеструке секвенце змије постоји са максималном дужином штампања било којег од њих.
Снаке секвенце чине суседне бројеве у мрежи тако да за сваки број број са десне стране или број испод њега је +1 или -1 његова вредност. На пример, ако сте на локацији (к и) у мрежи, можете или померити како је (к и + 1) ако је тај број ± 1 или се креће доле довн тј. (К + 1 и) ако је тај број ± 1.
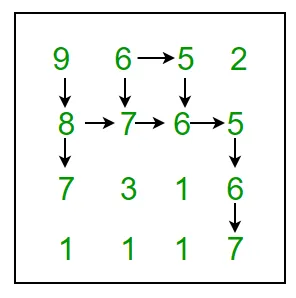
For example 9 6 5 2 8 7 6 5 7 3 1 6 1 1 1 7 In above grid the longest snake sequence is: (9 8 7 6 5 6 7)
Испод слике приказује све могуће стазе:
Топло вам препоручујемо да умањите свој претраживач и прво пробајте ово сами.
Идеја је да се користи динамичко програмирање. За сваку ћелију матрице задржавамо максималну дужину змије која се завршава у тренутној ћелији. Максимална дужина змија ће имати максималну вредност. Максимална ћелија вредности ће одговарати репу змије. Да бисмо одштампали змију, морамо да се вратимо од репа до краја назад до змијске главе.
Let T[i][i] represent maximum length of a snake which ends at cell (i j) then for given matrix M the DP relation is defined as T[0][0] = 0 T[i][j] = max(T[i][j] T[i][j - 1] + 1) if M[i][j] = M[i][j - 1] ± 1 T[i][j] = max(T[i][j] T[i - 1][j] + 1) if M[i][j] = M[i - 1][j] ± 1
Испод је примена идеје
C++// C++ program to find maximum length // Snake sequence and print it #include
// Java program to find maximum length // Snake sequence and print it import java.util.*; class GFG { static int M = 4; static int N = 4; static class Point { int x y; public Point(int x int y) { this.x = x; this.y = y; } }; // Function to find maximum length Snake sequence path // (i j) corresponds to tail of the snake static List<Point> findPath(int grid[][] int mat[][] int i int j) { List<Point> path = new LinkedList<>(); Point pt = new Point(i j); path.add(0 pt); while (grid[i][j] != 0) { if (i > 0 && grid[i][j] - 1 == grid[i - 1][j]) { pt = new Point(i - 1 j); path.add(0 pt); i--; } else if (j > 0 && grid[i][j] - 1 == grid[i][j - 1]) { pt = new Point(i j - 1); path.add(0 pt); j--; } } return path; } // Function to find maximum length Snake sequence static void findSnakeSequence(int mat[][]) { // table to store results of subproblems int [][]lookup = new int[M][N]; // initialize by 0 // stores maximum length of Snake sequence int max_len = 0; // store coordinates to snake's tail int max_row = 0; int max_col = 0; // fill the table in bottom-up fashion for (int i = 0; i < M; i++) { for (int j = 0; j < N; j++) { // do except for (0 0) cell if (i != 0 || j != 0) { // look above if (i > 0 && Math.abs(mat[i - 1][j] - mat[i][j]) == 1) { lookup[i][j] = Math.max(lookup[i][j] lookup[i - 1][j] + 1); if (max_len < lookup[i][j]) { max_len = lookup[i][j]; max_row = i; max_col = j; } } // look left if (j > 0 && Math.abs(mat[i][j - 1] - mat[i][j]) == 1) { lookup[i][j] = Math.max(lookup[i][j] lookup[i][j - 1] + 1); if (max_len < lookup[i][j]) { max_len = lookup[i][j]; max_row = i; max_col = j; } } } } } System.out.print('Maximum length of Snake ' + 'sequence is: ' + max_len + 'n'); // find maximum length Snake sequence path List<Point> path = findPath(lookup mat max_row max_col); System.out.print('Snake sequence is:'); for (Point it : path) System.out.print('n' + mat[it.x][it.y] + ' (' + it.x + ' ' + it.y + ')'); } // Driver code public static void main(String[] args) { int mat[][] = {{9 6 5 2} {8 7 6 5} {7 3 1 6} {1 1 1 7}}; findSnakeSequence(mat); } } // This code is contributed by 29AjayKumar
// C# program to find maximum length // Snake sequence and print it using System; using System.Collections.Generic; class GFG { static int M = 4; static int N = 4; public class Point { public int x y; public Point(int x int y) { this.x = x; this.y = y; } }; // Function to find maximum length Snake sequence path // (i j) corresponds to tail of the snake static List<Point> findPath(int[ ] grid int[ ] mat int i int j) { List<Point> path = new List<Point>(); Point pt = new Point(i j); path.Insert(0 pt); while (grid[i j] != 0) { if (i > 0 && grid[i j] - 1 == grid[i - 1 j]) { pt = new Point(i - 1 j); path.Insert(0 pt); i--; } else if (j > 0 && grid[i j] - 1 == grid[i j - 1]) { pt = new Point(i j - 1); path.Insert(0 pt); j--; } } return path; } // Function to find maximum length Snake sequence static void findSnakeSequence(int[ ] mat) { // table to store results of subproblems int[ ] lookup = new int[M N]; // initialize by 0 // stores maximum length of Snake sequence int max_len = 0; // store coordinates to snake's tail int max_row = 0; int max_col = 0; // fill the table in bottom-up fashion for (int i = 0; i < M; i++) { for (int j = 0; j < N; j++) { // do except for (0 0) cell if (i != 0 || j != 0) { // look above if (i > 0 && Math.Abs(mat[i - 1 j] - mat[i j]) == 1) { lookup[i j] = Math.Max( lookup[i j] lookup[i - 1 j] + 1); if (max_len < lookup[i j]) { max_len = lookup[i j]; max_row = i; max_col = j; } } // look left if (j > 0 && Math.Abs(mat[i j - 1] - mat[i j]) == 1) { lookup[i j] = Math.Max( lookup[i j] lookup[i j - 1] + 1); if (max_len < lookup[i j]) { max_len = lookup[i j]; max_row = i; max_col = j; } } } } } Console.Write('Maximum length of Snake ' + 'sequence is: ' + max_len + 'n'); // find maximum length Snake sequence path List<Point> path = findPath(lookup mat max_row max_col); Console.Write('Snake sequence is:'); foreach(Point it in path) Console.Write('n' + mat[it.x it.y] + ' (' + it.x + ' ' + it.y + ')'); } // Driver code public static void Main(String[] args) { int[ ] mat = { { 9 6 5 2 } { 8 7 6 5 } { 7 3 1 6 } { 1 1 1 7 } }; findSnakeSequence(mat); } } // This code is contributed by Princi Singh
def snakesequence(S m n): sequence = {} DP = [[1 for x in range(m+1)] for x in range(n+1)] a b maximum = 0 0 0 position = [0 0] for i in range(0 n+1): for j in range(0 m+1): a b = 0 0 p = 'initial' if(i > 0 and abs(S[i][j] - S[i-1][j]) == 1): a = DP[i-1][j] if(j > 0 and abs(S[i][j] - S[i][j-1]) == 1): b = DP[i][j-1] if a != 0 and a >= b: p = str(i-1) + ' ' + str(j) elif b != 0: p = str(i) + ' ' + str(j-1) q = str(i) + ' ' + str(j) sequence[q] = p DP[i][j] = DP[i][j] + max(a b) if DP[i][j] >= maximum: maximum = DP[i][j] position[0] = i position[1] = j snakeValues = [] snakePositions = [] snakeValues.append(S[position[0]][position[1]]) check = 'found' str_next = str(position[0]) + ' ' + str(position[1]) findingIndices = sequence[str_next].split() while(check == 'found'): if sequence[str_next] == 'initial': snakePositions.insert(0 str_next) check = 'end' continue findingIndices = sequence[str_next].split() g = int(findingIndices[0]) h = int(findingIndices[1]) snakeValues.insert(0 S[g][h]) snake_position = str(g) + ' ' + str(h) snakePositions.insert(0 str_next) str_next = sequence[str_next] return [snakeValues snakePositions] S = [[9 6 5 2] [8 7 6 5] [7 3 1 6] [1 1 10 7]] m = 3 n = 3 seq = snakesequence(S m n) for i in range(len(seq[0])): print(seq[0][i] '' seq[1][i].split())
function snakesequence(S m n) { let sequence = {} let DP = new Array(n + 1) for (var i = 0; i <= n; i++) DP[i] = new Array(m + 1).fill(1) let a = 0 b = 0 maximum = 0 let position = [0 0] for (var i = 0; i <= n; i++) { for (var j = 0; j <= m; j++) { a = 0 b = 0 let p = 'initial' if(i > 0 && Math.abs(S[i][j] - S[i-1][j]) == 1) a = DP[i-1][j] if(j > 0 && Math.abs(S[i][j] - S[i][j-1]) == 1) b = DP[i][j-1] if (a != 0 && a >= b) p = String(i-1) + ' ' + String(j) else if (b != 0) p = String(i) + ' ' + String(j-1) let q = String(i) + ' ' + String(j) sequence[q] = p DP[i][j] = DP[i][j] + Math.max(a b) if (DP[i][j] >= maximum) { maximum = DP[i][j] position[0] = i position[1] = j } } } let snakeValues = [] let snakePositions = [] snakeValues.push(S[position[0]][position[1]]) let check = 'found' let String_next = String(position[0]) + ' ' + String(position[1]) let findingIndices = sequence[String_next].split(' ') while(check == 'found') { if (sequence[String_next] == 'initial') { snakePositions.unshift(String_next) check = 'end' continue } findingIndices = sequence[String_next].split(' ') let g = parseInt(findingIndices[0]) let h = parseInt(findingIndices[1]) snakeValues.unshift(S[g][h]) let snake_position = String(g) + ' ' + String(h) snakePositions.unshift(String_next) String_next = sequence[String_next] } return [snakeValues snakePositions] } // Driver Code let S = [[9 6 5 2] [8 7 6 5] [7 3 1 6] [1 1 10 7]] let m = 3 let n = 3 let seq = snakesequence(S m n) for (var i = 0; i < seq[0].length; i++) console.log(seq[0][i] + '' seq[1][i].split(' '))
Излаз
Maximum length of Snake sequence is: 6 Snake sequence is: 9 (0 0) 8 (1 0) 7 (1 1) 6 (1 2) 5 (1 3) 6 (2 3) 7 (3 3)
Временски сложеност горњег раствора је О (М * Н). Помоћни простор који користи горњи раствор је О (М * Н). Ако није потребно да штампамо да се простор змија може даље смањити на О (Н) јер само користимо резултат из последњег реда.
јава веза мискл
