Пример 1:
Дизајнирајте НФА за прелазну табелу као што је дато у наставку:
| Садашње стање | 0 | 1 |
|---|---|---|
| →к0 | к0, к1 | к0, к2 |
| к1 | к3 | е |
| к2 | к2, к3 | к3 |
| →к3 | к3 | к3 |
Решење:
Дијаграм прелаза се може нацртати коришћењем функције мапирања као што је дато у табели.
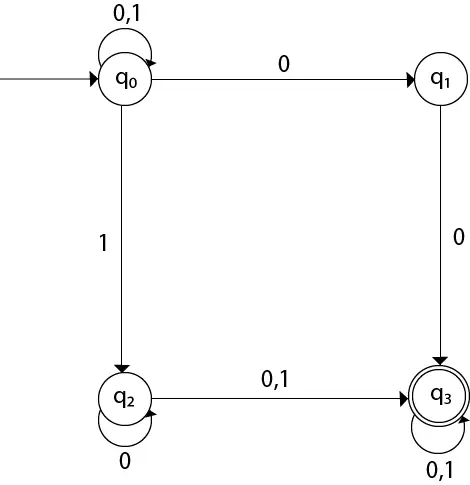
овде,
δ(q0, 0) = {q0, q1} δ(q0, 1) = {q0, q2} Then, δ(q1, 0) = {q3} Then, δ(q2, 0) = {q2, q3} δ(q2, 1) = {q3} Then, δ(q3, 0) = {q3} δ(q3, 1) = {q3} Пример 2:
Дизајн НФА са ∑ = {0, 1} прихвата све стрингове који се завршавају са 01.
колико је 10 од 1 милиона
Решење:

Дакле, НФА би била:

Пример 3:
Дизајнирајте НФА са ∑ = {0, 1} у којем двоструко '1' прати двоструко '0'.
Решење:
метод подстринга у Јави
ФА са дуплим 1 је следећи:

Одмах затим треба да буде дупло 0.
Онда,

Сада пре дуплог 1, може постојати било који низ од 0 и 1. Слично, после дуплог 0, може постојати било који низ од 0 и 1.
Стога НФА постаје:
колико тастера имају тастатуре

Сада узимајући у обзир низ 01100011
q0 → q1 → q2 → q3 → q4 → q4 → q4 → q4
Пример 4:
Дизајнирајте НФА у којем сви низови садрже подниз 1110.
Решење:
Језик се састоји од свих низова који садрже подниз 1010. Дијаграм делимичног прелаза може бити:

Сада као 1010 може бити подниз. Стога ћемо додати улазне 0 и 1 тако да се подниз 1010 језика може одржати. Стога НФА постаје:
рекурзија у Јави

Табела прелаза за горњи дијаграм прелаза може се дати у наставку:
| Садашње стање | 0 | 1 |
|---|---|---|
| →к1 | к1 | к1, к2 |
| к2 | к3 | |
| к3 | к4 | |
| к4 | к5 | *к5 | к5 | к5 |
Размотрите низ 111010,
δ(q1, 111010) = δ(q1, 1100) = δ(q1, 100) = δ(q2, 00)
Запео! Како нема путање од к2 за улазни симбол 0. Стринг 111010 можемо обрадити на други начин.
δ(q1, 111010) = δ(q2, 1100) = δ(q3, 100) = δ(q4, 00) = δ(q5, 0) = δ(q5, ε)
Пошто је стање к5 стање прихватања. Добијамо комплетно скенирање и стигли смо до коначног стања.
Пример 5:
Дизајн НФА са ∑ = {0, 1} прихвата све низове у којима је трећи симбол са десног краја увек 0.
греибацх нормална форма
Решење:

Тако добијамо трећи симбол са десног краја као увек '0'. НФА може бити:

Горња слика је НФА јер у стању к0 са улазом 0 можемо или прећи у стање к0 или к1.
