- ДФА се односи на детерминистичке коначне аутомате. Детерминистички се односи на јединственост израчунавања. Коначни аутомати се називају детерминистичким коначним аутоматима ако се машини чита улазни низ један по један симбол.
- У ДФА постоји само један пут за одређени унос из тренутног стања у следеће стање.
- ДФА не прихвата нулти потез, тј. ДФА не може да промени стање без било каквог улазног карактера.
- ДФА може да садржи више коначних стања. Користи се у лексичкој анализи у компајлеру.
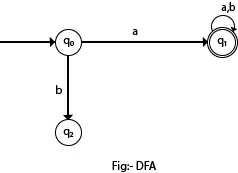
На следећем дијаграму можемо видети да из стања к0 за улаз а постоји само једна путања која иде до к1. Слично, од к0, постоји само један пут за улаз б који иде до к2.
Формална дефиниција ДФА
ДФА је колекција од 5 скупова истих као што смо описали у дефиницији ФА.
Q: finite set of states ∑: finite set of the input symbol q0: initial state F: final state δ: Transition function
Транзициона функција се може дефинисати као:
δ: Q x ∑→Q
Графичко представљање ДФА
ДФА се може представити диграфима који се називају дијаграм стања. У којима:
- Држава је представљена врховима.
- Лук означен улазним карактером приказује прелазе.
- Почетно стање је означено стрелицом.
- Коначно стање је означено двоструким кругом.
Пример 1:
Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q2} Решење:
Дијаграм транзиције:

Табела прелаза:
| Садашње стање | Следеће стање за улаз 0 | Следеће стање уноса 1 |
|---|---|---|
| →к0 | к0 | к1 |
| к1 | к2 | к1 |
| *к2 | к2 | к2 |
Пример 2:
ДФА са ∑ = {0, 1} прихвата све које почињу са 0.
Решење:

Објашњење:
- У горњем дијаграму можемо видети да на датом 0 као улазу за ДФА у стању к0 ДФА мења стање у к1 и увек иде у коначно стање к1 на почетном улазу 0. Може да прихвати 00, 01, 000, 001... итд. Не може прихватити ниједан стринг који почиње са 1, јер никада неће ићи у коначно стање на низу који почиње са 1.
Пример 3:
ДФА са ∑ = {0, 1} прихвата све које се завршавају са 0.
Решење:

Објашњење:
У горњем дијаграму можемо видети да на датом 0 као улазу за ДФА у стању к0, ДФА мења стање у к1. Може прихватити било који стринг који се завршава са 0 као што је 00, 10, 110, 100....итд. Не може прихватити ниједан стринг који се завршава са 1, јер никада неће прећи у коначно стање к1 на 1 улаз, тако да стринг који се завршава са 1, неће бити прихваћен или ће бити одбијен.
